EEPW论坛

逻辑函数的卡诺图化简法

　　由前面的学习得知，利用代数法可以使逻辑函数变成较简单的形式。但要求熟练掌握逻辑代数的基本定律，而且需要一些技巧，特别是经化简后得到的逻辑表达式是否是最简式较难确定。运用卡诺图法可以较简便的方法得到最简表达式。但首先需要了解最小项的概念。

一、最小项的定义及其性质

1.最小项的基本概念

　　由A、B、C三个逻辑变量构成的许多乘积项中有八个被称为A、B、C的最小项的乘积项，它们的特点是
　　1. 每项都只有三个因子
　　2. 每个变量都是它的一个因子
　　3. 每一变量或以原变量(Ａ、Ｂ、Ｃ)的形式出现，或以反（非）变量(Ａ、Ｂ、Ｃ)的形式出现，各出现一次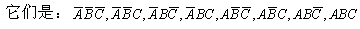
　　一般情况下，对ｎ个变量来说，最小项共有2ⁿ个，如n＝3时，最小项有2³＝8个

2.最小项的性质

　　为了分析最小项的性质，以下列出３个变量的所有最小项的真值表。

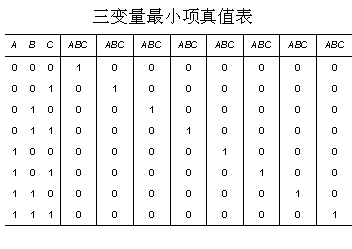
由此可见，最小项具有下列性质：
　　（1）对于任意一个最小项，只有一组变量取值使得它的值为1，而在变量取其他各组值时，这个最小项的值都是0。
　　（2）不同的最小项，使它的值为1的那一组变量取值也不同。
　　（3）对于变量的任一组取值，任意两个最小项的乘积为0。
　　（4）对于变量的任一组取值，全体最小项之和为1。

3.最小项的编号

　　最小项通常用m_i表示，下标i即最小项编号 ，用十进制数表示。以ABC为例，因为它和011相对应，所以就称ABC是和变量取值011相对应的最小项，而011相当于十进制中的3，所以把ABC记为m₃按此原则，3个变量的最小项

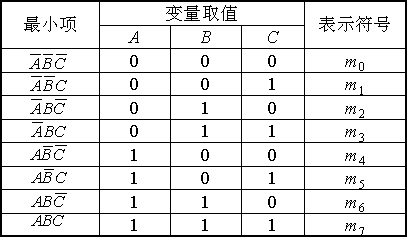
二、逻辑函数的最小项表达式

　　利用逻辑代数的基本公式，可以把任一个逻辑函数化成一种典型的表达式，这种典型的表达式是一组最小项之和，称为最小项表达式
。下面举例说明把逻辑表达式展开为最小项表达式的方法。例如，要将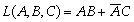化成最小项表达式,这时可利用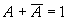的基本运算关系,将逻辑函数中的每一项都化成包含所有变量A、B、C的项，然后再用最小项下标编号来代表最小项，即

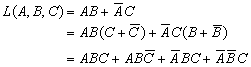
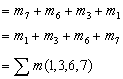
　　又如，要将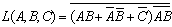 化成最小项表达式，可经下列几步：
　　（1）多次利用摩根定律去掉非号 ，直至最后得到一个只在单个变量上有非号的表达式；
　　（2）利用分配律除去括号，直至得到一个与或表达式；

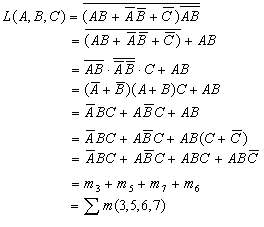
　　（3）在以上第5个等式中，有一项AB不是最小项（缺少变量C），可用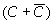乘此项，正如第6个等式所示。
　　由此可见，任一个逻辑函数都可化成为唯一的最小项表达式。

三、用卡诺图表示逻辑函数

1.卡诺图的引出

　　一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个特定的方格图内，此方格图称为卡诺图。
　　卡诺图是逻辑函数的一种图形表示。
　　下面从讨论一变量卡诺图开始，逐步过渡到多变量卡诺图。
　　大家知道，n个变量的逻辑函数有2ⁿ个最小项 ，因此一个变量的逻辑函数有两个最小项。
　　比如有一个变量Ｄ，其逻辑函数Ｌ的最小项表达式为：

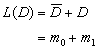
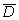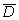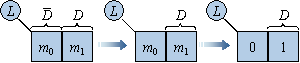
　　其中Ｄ和是两个最小项，分别记为m₁和m₀，即m₀=D，m₁=D。这两个最小项可用两个相邻的方格来表示，如下图所示。方格上的Ｄ和分别表示原变量和非变量。为了简明起见，非变量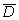可以不标出，只标出原变量Ｄ。但是还可以进一步简化，也就是将m₀，m₁只用其下标编号来表示。

　　若变量的个数为两个，则最小项个数为2²=4项，函数的最小项表达式为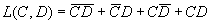
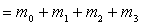
　　由于有４个最小项，可用４个相邻的方格来表示。这４个方格可以由折叠了的１变量卡诺图展开来获得，如下图所示，变量Ｄ标在图的底下，标的规律符合展开的规律，即中间两格底下为Ｄ，两边的两格底下为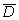。而变量Ｃ可标在展开后新的两个方格的顶上,以保持左边的第一格仍为m₀项，即维持展开前两方格最小项序号不改变。由图中可看到一个规律：新的方格内最小项的编号比对应的原方格增加了2^n-1＝2^2-1＝2。按照这个规律折叠时，方格1后面为方格３,方格０后面为方格２，展开后即得图示的２变量卡诺图。

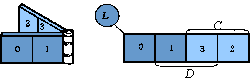
综上所述，可归纳“折叠展开”的法则如下：
　　①新增加的方格按展开方向应标以新变量。
　　②新的方格内最小项编号应为展开前对应方格编号加2^n-1。
　　按照同样的方法，可从折叠的２变量卡诺图展开获得３变量卡诺图。３变量逻辑函数L(B, C, D)应有８个最小项，可用８个相邻的方格来表示。新增加的 ４个方格按展开方向应标以新增加的变量B（以区别于原来的变量C、D）。而且，新增加的方格内最小项的编号为展开前对应方格编号加2^n-1=2^3-1=4，这样即可获得３变量卡诺图如下：

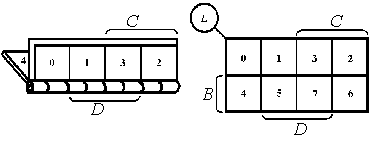
　　同理，可得４变量卡诺图，如下图所示。

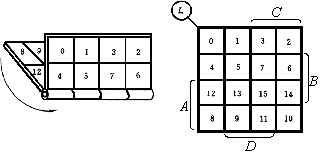
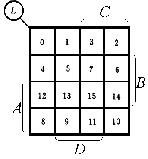
　　在使用时，只要熟悉了卡诺图上各变量的取值情况（即方格外各变量A、B、C、D等取值的区域），就可直接填入对应的最小项。

　　将上图中的数码编号与最小项的编号——对应，可以得到下面这种形式的卡诺图。

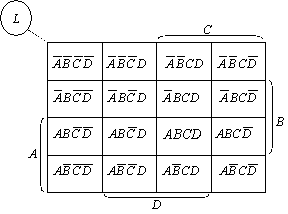
2.卡诺图的特点

　　上面所得各种变量的卡诺图，其共同特点是可以直接观察相邻项
。也就是说，各小方格对应于各变量不同的组合，而且上下左右在几何上相邻的方格内只有一个因子有差别，这个重要特点成为卡诺图化简逻辑函数的主要依据。在卡诺图水平方向的同一行里，最左和最右端的方格也是符合上述相邻规律的，例如，m₄和m₆的差别仅在C和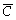。同样，垂直方向同一列里最上端和最下端两个方格也是相邻的，这是因为都只有一个因子有差别。这个特点说明卡诺图呈现循环邻接的特性。

3.已知逻辑函数画卡诺图

　　根据逻辑函数的最小项表达式和卡诺图的一般形式，就可以得到相应的卡诺图。
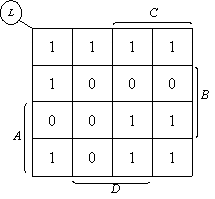
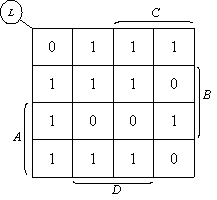
　例如，要画出逻辑函数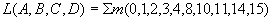的卡诺图时，可根据４变量卡诺图，对上列逻辑函数最小项表达式中的各项，在卡诺图相应方格内填入１，其余填入０，即可得到如下图所示的Ｌ的卡诺图。

例：画出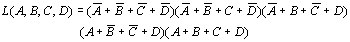
的卡诺图
解：
　　（1）利用摩根定律，可以将上式化简为：

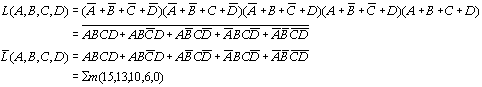
　　（2）因上式中最小项之和为Ｌ，故对Ｌ中的各最小项，在卡诺图相应方格内应填入０，其余填入１，即得下图所示的卡诺图。

四、用卡诺图化简逻辑函数

1.化简的依据

　　我们知道，卡诺图具有循环邻接的特性，若图中两个相邻的方格均为1，则这两个相邻最小项的和将消去一个变量。
　　比如４变量卡诺图中的方格５和方格７，它们的逻辑加是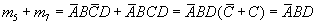，项消去了变量Ｃ，即消去了相邻方格中不相同的那个因子。若卡诺图中４个相邻的方格为１，则这４个相邻的最小项的和将消去两个变量，如上述４变量卡诺图中的方格２、３、７、６，它们的逻辑加是

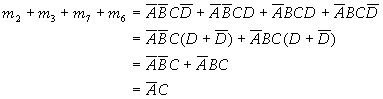
　　消去了变量Ｂ和Ｄ，即消去相邻４个方格中不相同的那两个因子
，这样反复应用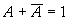的关系，就可使逻辑表达式得到简化。这就是利用卡诺图法化简逻辑函数的某本原理。

2.化简的步骤

用卡诺图化简逻辑函数的步骤如下：
　　（1）将逻辑函数写成最小项表达式。
　　（2）按最小项表达式填卡诺图 ，凡式中包含了的最小项，其对应方格填1，其余方格填0。
　　（3）合并最小项，即将相邻的1方格圈成一组（包围圈），每一组含2ⁿ个方格，对应每个包围圈写成一个新的乘积项。
　　（4）将所有包围圈对应的乘积项相加。
　　有时也可以由真值表直接填卡诺图，以上的（1）、（2）两步就合为一步。

画包围圈时应遵循以下原则：
　　（1）包围圈内的方格数必定是2ⁿ个，n等于0、1、2、3、…。
　　（2）相邻方格包括上下底相邻，左右边相邻和四角相邻。
　　（3）同一方格可以被不同的包围圈重复包围 ，但新增包围圈中一定要有新的方格，否则该包围圈为多余。
　　（4）包围圈内的方格数要尽可能多，包围圈的数目要尽可能少。

　　化简后，一个包围圈对应一个与项（乘积项），包围圈越大，所得乘积项中的变量越少。实际上，如果做到了使每个包围圈尽可能大
，结果包围圈个数也就会少，使得消失的乘积项个数也越多，就可以获得最简的逻辑函数表达式。下面通过举列来熟悉用卡诺图化简逻辑函数的方法。

　　例: 一个逻辑电路的输入是４个逻辑变量Ａ、Ｂ、Ｃ、Ｄ ，它的真值表如下，用卡诺图法求化简的与一或表达式及与非一与非表达式。

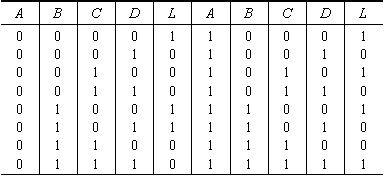
解：
　　（1）由真值表画出卡诺图，如下图所示。

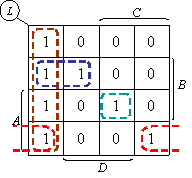
　　（2）画包围圈合并最小项，得简化的与一或表达式。

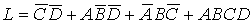
　　（3） 求与非一与非表达式。

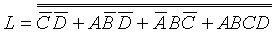
　　二次求非然后利用摩根定律得

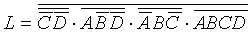
　　利用卡诺图表示逻辑函数式时，如果卡诺图中各小方格被１占去了大部分，虽然可用包围１的方法进行化简，但由于要重复利用１项
，往往显得零乱而易出错。这时采用包围０的方法化简更为简单。即求出非函数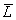再对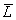求非，其结果相同，下面举例说明。

例：化简下列逻辑函数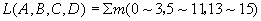

解：
　　（1）由Ｌ画出卡诺图，如图所示。

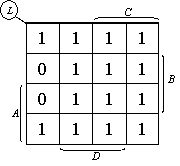
　　（2）用包围１的方法化简，如下图所示，得

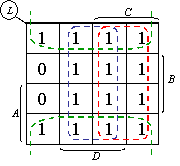
　　所以有：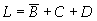

　　（3）用包围０的方法化简，如图所示，

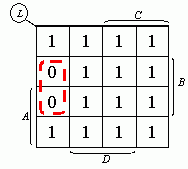
　　根据图得到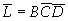：，两边去反后可得：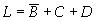
　　两种方法得到的结果是相同的。
　　实际中经常会遇到这样的问题，在真值表内对应于变量的某些取值下，函数的值可以是任意的，或者这些变量的取值根本不会出现，这些变量取值所对应的最小项称为无关项或任意项。
　　无关项的意义在于，它的值可以取０或取１，具体取什么值，可以根据使函数尽量得到简化而定。