EEPW论坛

决策树是机器学习中使用的最流行和功能最强大的分类算法之一。顾名思义，决策树用于根据给定的数据集做出决策。也就是说，它有助于选择适当的特征以将树分成类似于人类思维脉络的子部分。

为了有效地构建决策树，我们使用了熵/信息增益和基尼不纯度的概念。让我们看看什么是基尼不纯度，以及如何将其用于构建决策树吧。

什么是基尼不纯度？

基尼不纯度是决策树算法中用于确定根节点的最佳分割以及后续分割的方法。这是拆分决策树的最流行、最简单的方法。它仅适用于分类目标，因为它只执行二进制拆分。

基尼不纯度的公式如下：

基尼不纯度越低，节点的同质性越高。纯节点（相同类）的基尼不纯度为零。以一个数据集为例，计算基尼不纯度。

该数据集包含18个学生，8个男孩和10个女孩。根据表现将他们分类如下：

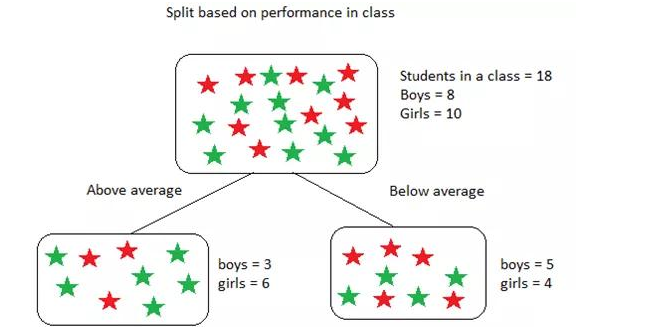
上述基尼不纯度的计算如下：

上述计算中，为了找到拆分（根节点）的加权基尼不纯度，我们使用了子节点中学生的概率。对于“高于平均值”和“低于平均值”节点，该概率仅为9/18，这是因为两个子节点的学生人数相等，即使每个节点中的男孩和女孩的数量根据其在课堂上的表现有所不同，结果亦是如此。

如下是使用基尼不纯度拆分决策树的步骤：

类似于在熵/信息增益的做法。对于每个拆分，分别计算每个子节点的基尼不纯度。

计算每个拆分的基尼不纯度作为子节点的加权平均基尼不纯度。

选择基尼不纯度值最低的分割。

重复步骤1-3，直到获得同类节点。

基尼不纯度小总结：

有助于找出根节点、中间节点和叶节点以开发决策树。

被CART（分类和回归树）算法用于分类树。

当节点中的所有情况都属于一个目标时，达到最小值（零）。

总而言之，基尼不纯度比熵/信息增益更受青睐，因为它公式简单且不使用计算量大而困难的对数。