EEPW论坛

放大器的非线性失真是指输入信号在经过放大器后所产生的输出信号中包含其他频率分量的信号，由于非线性失真导致了原信号所包含的信息发生了畸变，这会给信号处理带来很大困难。放大器失真的原因主要有两个：一是放大器件的工作点进入了特性曲线的非线性区，使输入信号和输出信号不再保持线性关系；二是放大器的频率特性不好，对输入信号中不同频率成分的增益或延时不同。放大器的失真会影响信号的质量和稳定性，因此需要采取一些措施来消除或减小失真，如选择合适的偏置电压、负反馈、滤波、屏蔽等。在一定程度上，每个放大器都是非线性的，并且在大多数情况下很难准确确定放大器的非线性方程。但是，如果在所感兴趣的信号频率范围内，非线性信号的功率非常小，则可以将放大器看作是线性的。谐波失真是一种发生在输入信号频率谐波上的失真，其频率为输入信号频率的整数倍。谐波失真是由非线性的传递函数产生的，如果假定传递函数是平稳的，如不随时间变化，而且输入信号呈现周期性，那么输出也将是一个周期信号。频域上，周期信号的傅里叶级数由基波周期频率的谐波组成，对于一个周期输入信号，当输入输出之间的函数关系不随时间变化，都不会出现非谐波失真。

谐波的产生是由于非线性负载的存在，导致了电流与电压之间形成了非线性关系，它可以用一个二阶多项式来描述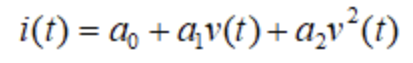：其中i(t)是电流，v(t)是电压，a0,a1,a2是常数。如果电压是一个正弦波，例如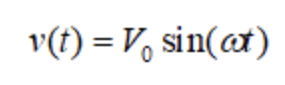：其中，V0是电压的幅值，ω是电压的角频率。将电压代入电流的表达式，可以得到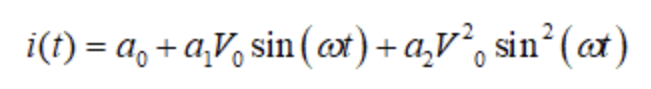：可以将三角函数的公式代入电流的表达式，得到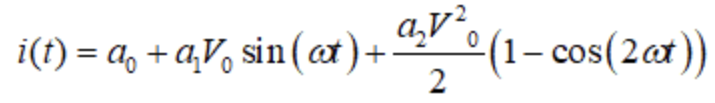：从表达式可以看出，电流中除了包含基波频率ω的分量，还包含二次谐波频率2ω的分量，其幅值与a2和V0平方成正比。因此，二阶多项式可以用来表示谐波的产生，而二次谐波的强度与电压的平方有关。若输入输出电压特性呈现出更为复杂的关系，那么将导致更高次谐波的出现。

测量方法

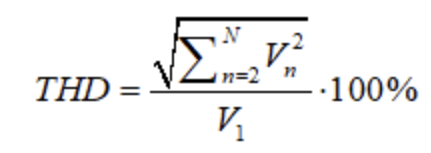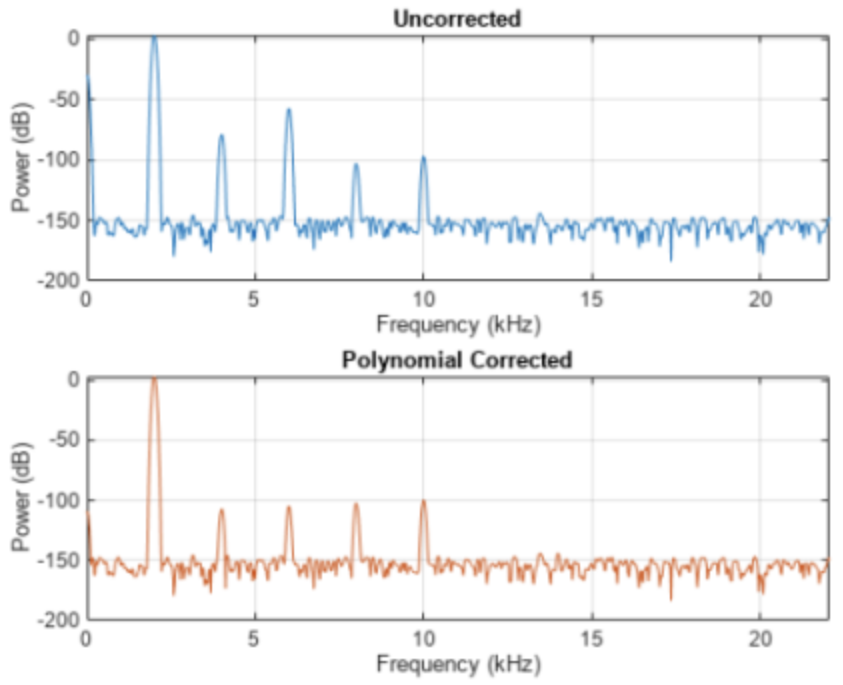
对于放大器这样的器件，常用指标是总谐波失真（Total Harmonic Distortion，THD）测量方法与公式如下：测量方法：产生一个频谱纯净的单频正弦波信号作为输入，用一个频谱分析仪观察输出信号的频谱，记录下基波和各阶谐波的幅度。测量公式：总谐波失真(THD)为所有谐波的均方根值与基波的均方根值的比值，通常用百分比或分贝表示。计算公式为：其中，V1是基波的均方根值，Vn是第n阶谐波的均方根值，N是考虑的最高阶数。若需要转换成dB，是20*log10(.)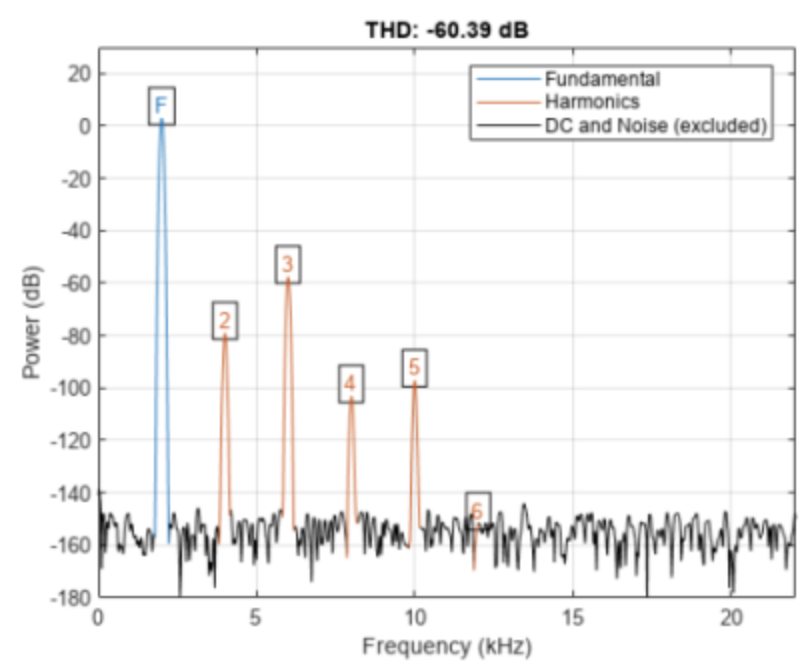Matlab中有直接计算THD的函数：thd(x)。有时可以对放大器的一些非线性进行校正。如果放大器的输出经过数字化，可以通过对捕获的输出进行数字后处理并对非线性进行数学校正来还原更好的动态范围。发现使用多项式校正时，第二个和第三个谐波会显著降低。