RLC电路是由电阻器、电感器和电容器构成的电子电路,它能够对特定频率的信号进行增强或滤除,在信号滤波与整形领域已得到有效应用。由于RLC电路串联和并联时的阻抗和瞬态响应特性不同,因此为它们在信号处理领域的多样化应用提供了可能。此外,理解并合理调节RLC电路的阻尼和Q值,是设计高性能、高能效电路不可或缺的环节。本文将从RLC电路的基本原理到应用技术,进行通俗易懂的解析。
1什么是RLC电路
RLC电路是由电阻器(R)、电感器(L)、电容器(C)构成的电子电路。这些元件可采用串联或并联方式连接。串联时,电流沿单一方向流动,依次通过各个元件;并联时,电流分流,同时流过各个元件。
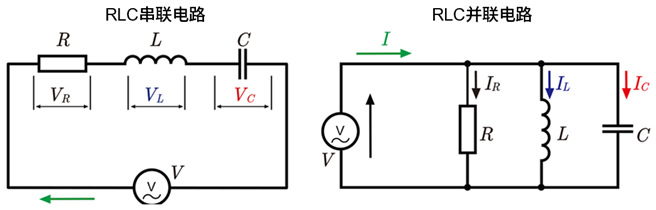
RLC电路的构成
| 元件 | 在电路中的作用 |
| 电阻器(R) | 对电流的流动产生阻碍作用,使电路产生阻尼(即能量衰减),这种能量消耗特性对电路的整体行为具有重要影响。 |
| 电感器(L) | 抵抗电流的变化,通过磁场储存能量。电感器的特性会影响电路的时间响应特性,起到延迟电流流动的作用。 |
| 电容器(C) | 抵抗电压的变化,储存电荷。电容器通过响应电压变化完成能量的储存与释放,决定电路的动态特性。 |
RLC电路的工作原理
在RLC电路中,能量在电容器与电感器之间持续转换。在能量从电容器传递至电感器,再从电感器传递回电容器的过程中,电路内的电流和电压会随时间变化。这种能量交换对电路的谐振特性和振荡特性有着重大影响。
谐振频率
RLC电路的谐振频率表达式如下:
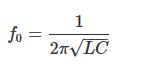
谐振角频率的表达式如下:
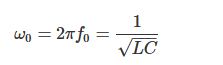
在该谐振频率下,电抗相互抵消,电路的LC分量相消。
2RLC串联电路
RLC串联电路是由电阻(R)、电感(L)、电容(C)串联连接而成的电路。该电路对交流(AC)信号的响应具有重要意义,广泛应用于滤波器(如带通滤波器)和振荡器(如LC振荡器)等设备中。阻抗是电阻与电抗的复合量,同时也反映了电路中电流与电压的相位差。RLC电路具有谐振、Q值等特性,这些特性在电路设计与应用中发挥着重要作用。
RLC串联电路与电压
在RLC串联电路中,流过各元件的电流相同,但各元件上的电压降存在差异。
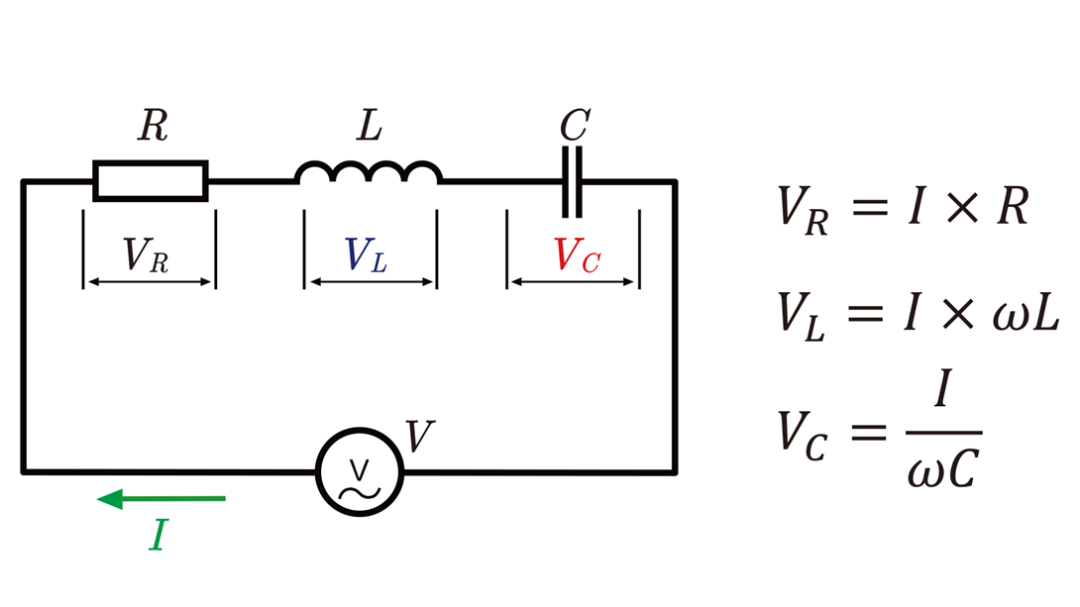
RLC串联电路中各元件的电压降可通过以下公式计算:
| 电阻器 | VR=I×R |
| 电感器 | VL=I×ωL |
| 电容器 | VC=I/ωC |
RLC串联电路中的相位差
由于电感器与电容器的电压相位会随频率变化,因此会对电流与电压的关系产生影响。
要点
相位差:电感器的电压超前电流90度,而电容器的电压滞后电流90度。
RLC串联电路的电压取决于各元件的特性和频率。若要了解准确的电压降,需考虑角频率及各元件的参数值,同时相位差的影响也至关重要。可根据这些因素对RLC串联电路的特性进行分析,并了解电压的分布情况。
RLC串联电路的阻抗
在RLC串联电路中,阻抗是表示电路电流与电压比值的复数。阻抗Z的计算公式如下:
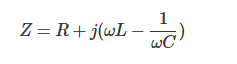
该阻抗Z的实部代表电阻R,虚部则体现电感与电容的作用。当角频率ω变化时,感抗分量ωL与容抗分量1/ωC的作用也会随之改变,进而导致阻抗发生变动。
阻抗计算需采用欧姆定律V=I×Z的复数形式。其中V为电压,I为电流。通过这一公式,可对特定频率下RLC电路的特性进行解析;同时,通过分析阻抗的实部与虚部,还可了解电路的阻性或电抗性特征。
此外,阻抗Z的模表示复数的模值,其计算公式如下:
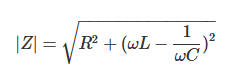
模 |Z|代表电路整体阻抗的大小,即电压与电流比值的幅值,用于综合评估实部(电阻)和虚部(电抗)共同产生的影响。
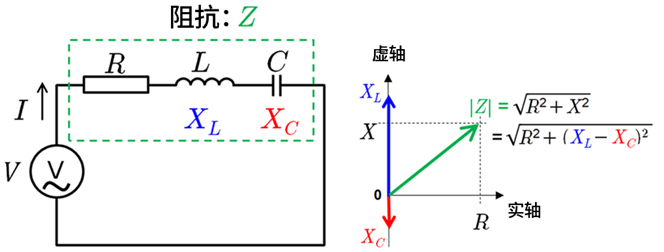
RLC串联电路的阻抗是用复数表示的电路电流与电压的比值,包含电阻和电抗的作用。阻抗的模表示其大小,对于了解电路的整体响应情况至关重要。理解阻抗,可在电路设计和信号处理等众多领域开展实际应用。
RLC串联电路的Q值
RLC串联电路中谐振特性的锐度与瞬态响应密切相关。瞬态响应是指输入信号发生变化时电路的反应方式。Q值表示谐振频率下电流通过的难易程度,反映电路瞬态响应的品质。Q值越高,表明电路对特定频率的响应越敏锐,且不易受其他频率的影响。
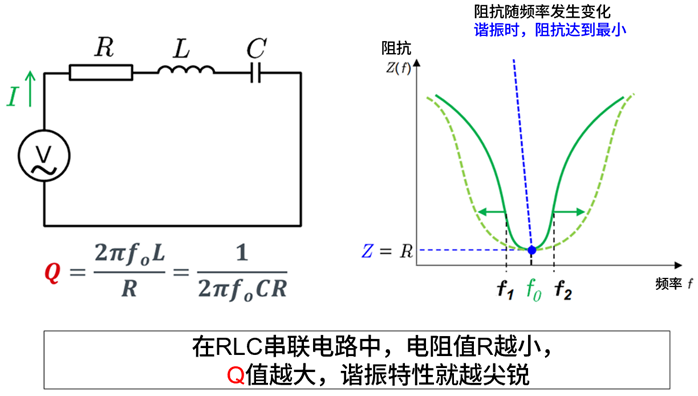
Q值的计算
RLC串联电路的Q值计算公式如下:
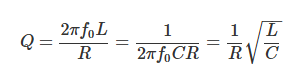
需注意的是,上述公式的推导运用了以下谐振条件(并联谐振)的关系:
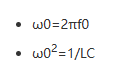
电阻值与Q值的关系
在RLC串联电路中,电阻值R越小,Q值越大,谐振特性也越尖锐。这是因为较小的电阻值会减少电路的能量损耗,使得电路对特定频率的响应更强。
RLC串联电路及其特性
RLC串联电路由电阻器(R)、电感器(L)和电容器(C)串联组成。这种电路的谐振频率(ω0)定义为1/√LC。在谐振频率下,阻抗的虚部为零,阻抗(|Z|)达到最小值R。
RLC串联电路的瞬态响应受Q值影响显著,而Q值取决于电路的电阻值。Q值越高,电路的谐振特性越尖锐,对特定频率的响应也就越强。
3RLC并联电路
RLC并联电路是由电阻(R)、电感(L)、电容(C)并联连接而成的电气电路,可在特定频率下发生谐振。利用这一特性可有效进行信号滤波和频率选择。此外,在谐振频率下,电路阻抗达到非常大的程度,能量效率随之提高,因此在高频电路及无线通信设备的设计中颇具实用价值。
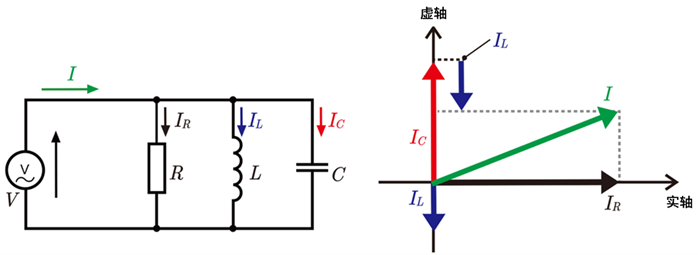
RLC并联电路的导纳
导纳可理解为阻抗的倒数,在并联电路中是一个尤为重要的概念。RLC并联电路的导纳是综合反映电路各组成部分影响的指标。
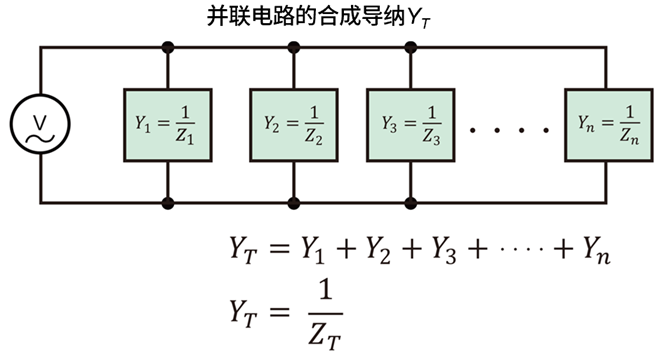
RLC并联电路的导纳表达式如下:
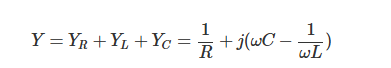
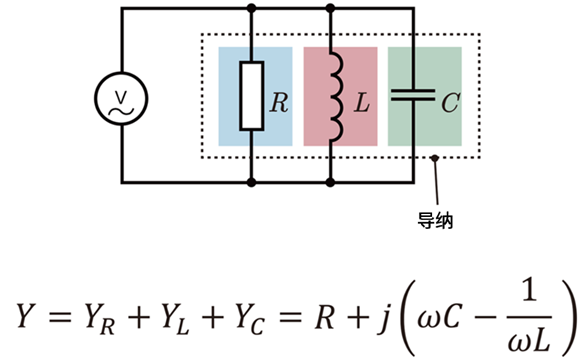
导纳的特征
逆阻抗特性:导纳的功能相当于阻抗的倒数。
阻抗表示对电流流动的“阻碍作用”,而导纳则表示电流的“通过难易程度”。
并联电路特性:导纳反映了各元件对电路总电流的贡献情况。
频率依赖性:导纳具有频率依赖性。
这是由于电容和电感的影响会随频率变化而改变。
通过导纳,能够更深入地理解RLC并联电路的工作原理,并分析电路在特定频率下的特性。
RLC并联电路的阻抗与导纳
在RLC并联电路中,阻抗定义为导纳(逆阻抗)的倒数。导纳的模表达式如下:
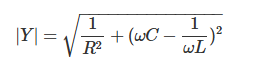
其中,R为电阻,L为电感,C为电容,ω为角频率。
因此,RLC并联电路阻抗的模∣Z∣可通过导纳的倒数求得,表达式如下:
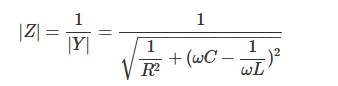
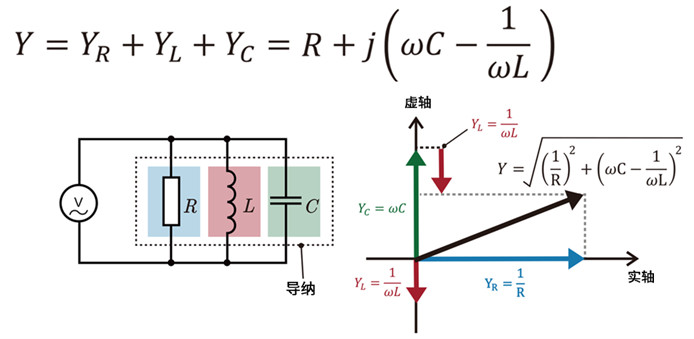
在谐振频率f0下,电感与电容的电抗相互抵消,以下条件成立:
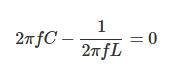
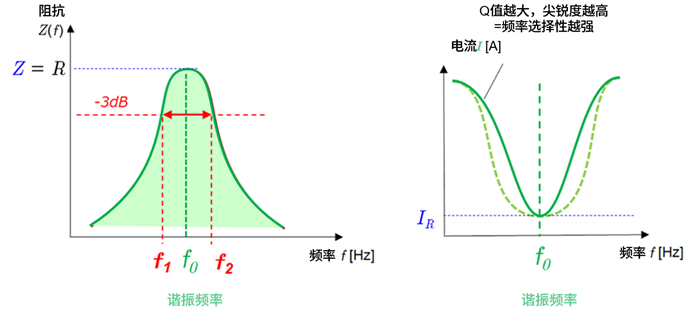
因此,在谐振频率下,阻抗的模∣Z∣达到最大。这一特性是RLC并联电路的重要特征,在滤波器及谐振电路等设计中具有重要意义。
此外,谐振状态下电路中电流的模∣I∣最小。这是由于并联电路在谐振频率下的阻抗最大所致。
RLC并联电路中的电流
在这里我们利用欧姆定律计算RLC并联电路的电流。
欧姆定律的表达式为:I=Y×V。其中,Y为导纳(阻抗的倒数),V为电压。举例来说,当电压V= 10、导纳Y= 0.224(相位角−63.4°)时,电流I的计算过程如下:
将导纳Y用三角函数表示为:
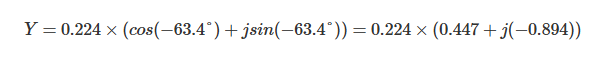
由于电压V的相位角为0°,因此:
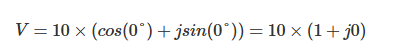
电流I为:
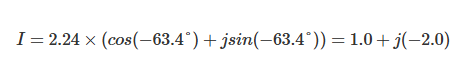
计算结果显示,电流的实部为1.0A,虚部为-2.0A,由此可确定RLC并联电路中电流的大小与相位角。
RLC并联电路与带宽的关系
RLC并联电路的带宽表征以谐振频率为中心的阻抗及导纳变化,决定了电路能有效工作的频率范围。下面讲解RLC并联电路与带宽的关系。
带宽指电路能有效工作的频率范围。对于RLC并联电路,相对于谐振频率(f0)的带宽(BW)定义如下:
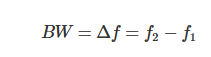
或
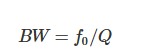
其中,ω1和ω2是以谐振频率为中心、阻抗等于最大值一半时的频率。带宽受以下因素影响:
电阻(R)
电阻值越小,谐振频率处的阻抗变化越陡峭,带宽越窄。反之,电阻值越大,带宽越宽。
品质因数(Q値)
品质因数(Q)的定义式如下:
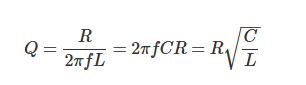
高Q值意味着窄带宽和尖锐谐振,低Q值则对应宽带宽和平缓谐振。
RLC并联电路的带宽由电感、电容及电阻值决定。谐振频率处的阻抗变化与品质因数共同决定了电路对频率的响应特性。高品质因数对应尖锐谐振与窄带宽,低品质因数则对应宽带宽。
理解上述关系后,可根据特定用途设计电路。例如,在滤波电路中为了只让特定频率带宽通过,会要求具有较高的Q值。
RLC电路的串联与并联
无论是串联还是并联形式的RLC电路,其共通的基本原理都在于电流与电压的关系,以及电阻器(R)、电感器(L)、电容器(C)这三个基本元件的作用。这些元件决定了电流的流向和电压的变化,因此在两种电路中都占据重要地位。
串联电路与并联电路的共同特性
RLC串联电路与并联电路在某些特定要素和现象上具有基本相似性。谐振、阻尼以及电路组成元件(电阻、电感、电容)的基本作用,在两种电路中是一致的。
谐振与固有频率
串联和并联RLC电路均具有谐振特性。谐振是指在特定频率(称为固有频率或谐振频率)下,电路响应达到最大的现象。该谐振频率由电路元件的参数值决定。尽管两种电路的谐振频率可能不同,但谐振的基本概念是一致的。
阻尼效应
电阻器产生的阻尼效应在串联电路和并联电路中均存在。电阻器通过限制电流流动、引起能量衰减,从而影响电路的表现。这一现象是电阻器将能量以热量形式消耗掉而引起的。
电路的基本特性
RLC电路的基本特性(如电流流向和电压分布)在串联电路与并联电路中具有共性。尽管串联电路中的“阻抗”与并联电路中的“导纳”是不同概念,但它们都是用于表示电流与电压关系的手段,且均植根于基本的电路原理。
串联电路与并联电路的区别
阻抗与导纳
串联电路与并联电路的主要区别之一在于阻抗(Z)与导纳(Y)的作用及表达式。RLC串联电路的阻抗是各元件(电阻器、电感器、电容器)阻抗的总和,而在RLC并联电路中,导纳更为重要,其值为各元件导纳(阻抗的倒数)的总和。这些差异对于理解电流与电压的关系至关重要。
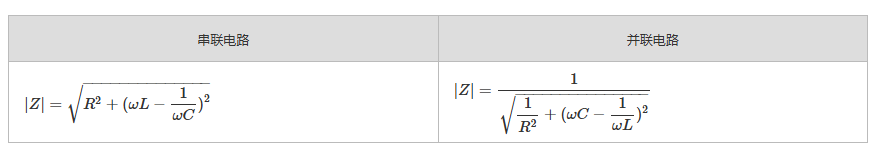
电流流向
串联电路中,相同的电流流过所有元件;而在并联电路中,总电流会分流到各元件,流过每个元件的电流各不相同。
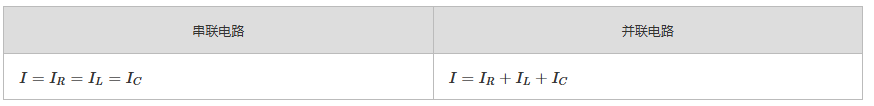
电压降与电压分布
串联电路中,电压沿各元件产生电压降,电压分布取决于各元件的特性;而在并联电路中,所有元件两端的电压相同,电压分布是均匀的。
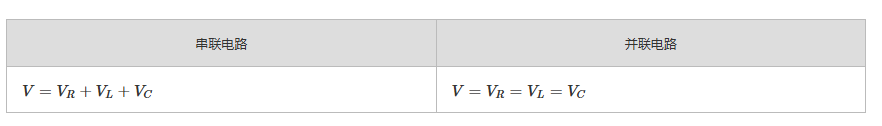
频率响应与带宽
RLC串联电路与并联电路的频率响应存在差异。由于谐振频率的计算方法不同,且影响电路带宽的元件配置有别,两者的工作特性也不相同。
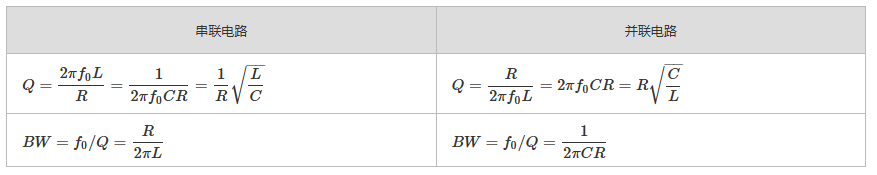
瞬态响应
RLC串联电路与并联电路的瞬态响应也存在差异。串联电路中,瞬态现象产生于能量从一个元件向另一个元件转移的过程;而并联电路中,由于能量分布方式不同,瞬态现象的表现形式也有所区别。
RLC串联电路与并联电路在阻抗与导纳、电流流向、电压分布、频率响应及瞬态响应等方面存在明显差异。这些差异是电路设计与分析中需要重点考虑的因素。
RLC电路的谐振:概念与公式解析
RLC电路的谐振是指电能与磁能交换速率达到峰值的状态。这种状态由电容与电感之间的能量谐振引发,仅在特定频率下出现。谐振概念在电子电路的设计与分析中非常重要。
谐振的数学表达
RLC串联电路的谐振可通过以下方程表示:
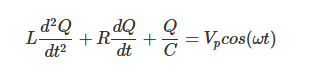
其中,Q为电容器的电荷量,L为电感,R为电阻,C为电容,Vp为峰值电压,ω为角频率。
该方程描述了RLC电路的动态特性,包含了电荷量随时间的变化关系。
平均功率公式
谐振状态下的平均功率PAVG如下式所示:
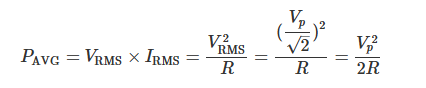
其中,IRMS为有效值电流,Z为电路的阻抗。
Q值(品质因数)
Q值表示能量存储能力与能量耗散能力的比值,是评估谐振时电路性能的指标。
这个Q值用于量化电路在谐振状态下的响应锐度。Q值越高,谐振峰越窄,能量损耗越少。
综上,RLC电路的谐振现象是电路设计中实现优化及提升特定频率下性能的关键要素。
RLC电路的固有频率
RLC电路的固有频率是指包含电阻器(R)、电感器(L)、电容器(C)在内的电路所产生的自然振荡频率。该固有频率由电路特性决定,尤其在能量于储能元件(线圈和电容器)之间转移时发挥重要作用。
固有频率的推导
为求RLC电路的固有频率,应用基尔霍夫定律可得到如下方程:
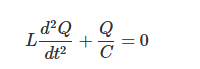
其中,L为电感,C为电容,Q为电容器的电荷量。
该二阶微分方程称为“简谐振动方程(harmonic oscillator equation)”,RLC电路的固有频率ωR计算公式如下:
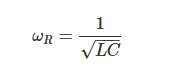
此式表明,固有频率取决于电感和电容的数值,由这两个参数共同决定。固有频率是电路自由振荡时的频率,其前提是无外部驱动。
综上,RLC电路的固有频率是能量在电路中电感与电容间高效交换时的自然频率,是电路设计与分析中的重要参数。
电阻的阻尼影响
在RLC电路中,电阻器(R)是阻尼(能量衰减)的重要要素。应用基尔霍夫定律,RLC电路的方程描述如下:
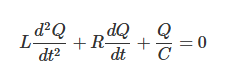
其中,L为电感,R为电阻,C为电容,Q为电容的电荷量。

阻尼的影响
阻尼可理解为振荡系统中的能量耗散。RLC电路中的电阻器会因电流通过产生焦耳热(能量损失),这种焦耳热导致能量耗散,进而影响振荡振幅的衰减。
弱阻尼(小R值):电路振荡持续时间更长,能量耗散较慢;
强阻尼(大R值):振荡迅速衰减,能量耗散较快。
由此可见,RLC电路中电阻器的重要作用是控制振荡的衰减(阻尼)。这对RLC电路的工作特性有着显著影响。
RLC电路(LC电路)的常见误解与错误认知
关于电路的工作原理及特性,常常存在一些常见误解和错误认知。下面将厘清RLC电路与LC电路的常见误解和错误认知,以加深正确理解。尤其针对LC电路谐振时的阻抗特性、Q值(品质因数)的含义、瞬态响应的理解等基础却易混淆的要点进行重点说明。
LC电路谐振时的阻抗
一种常见误解是认为LC电路处于谐振状态时具有最小阻抗。但实际上,LC电路谐振时,电感(L)与电容(C)的电抗相互抵消,仅剩余纯电阻分量。因此,LC电路的阻抗并非最小,而是等于电路内电阻分量的数值。
关于谐振频率与反谐振频率的混淆
另一种常见误解是将LC电路的谐振频率错误地称为“反谐振频率 ”。实际上,LC电路的谐振频率是指电路发生谐振、能量在电感器与电容器间高效交换时的频率。这一频率是表征电路特性的重要参数,通常称为“谐振频率”。
其他关于RLC及LC电路的常见误解与错误认知
对电感与电容储能方式的误解:
人们常对电感器和电容器的储能方式存在误解。电感器以磁场形式储存能量,电容器以电场形式储存能量。两者虽具有互补性,但并非完全相同,理解这一点至关重要。
对品质因数(Q值)的误解:
RLC电路的Q值是表征电路谐振特性的指标,但其含义常被误解。Q值越高,电路的带宽越窄,对谐振频率的敏感度越高;反之,Q值越低,电路的带宽越宽,频率响应越“平缓”。
对瞬态响应的误解:
RLC电路的瞬态响应(尤其是阻尼特性)有时会被简化或忽略。瞬态响应反映电路达到稳定状态前的动态特性,在滤波器及振荡系统中尤为重要。
对RLC电路用途的误解:
RLC电路的用途并非仅限于滤波器或振荡器,还广泛应用于电源管理、信号整形、振动分析等多个领域。不应低估RLC电路在特定应用中的重要性。
RLC电路在滤波器中的应用实例
RLC电路作为一种应用电路,可用来轻松去除不必要的噪声及增强特定信号成分。
低通滤波器、高通滤波器、带通滤波器等不同类型的滤波器,对应特定的频率特性,有助于根据用途实现最优的信号处理。
RLC电路与带宽BW
带宽BW表示RLC电路有效工作的频率范围。尤其在作为滤波器使用时,带宽指允许通过的信号的频率范围。带宽通常定义为增益降至最大增益的3dB(电压或电流为1/√2倍)以下时的频率范围。
带宽与RLC电路的关系
RLC电路的带宽因各元件参数值及其配置而异。当它作为在谐振频率(固有频率)附近具有峰值的带通滤波器工作时,其带宽非常重要。
计算公式
带宽BW可通过谐振频率数f0和品质因数Q计算。
一般表达式如下:
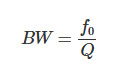
其中,f0为谐振频率,Q为品质因数。
品质因数Q的含义
Q值表征电路的选择性,Q值越高,意味着带宽越窄。
Q值的计算公式如下:
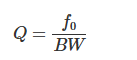
其中,BW为带宽。
RLC电路的带宽是决定滤波器性能的重要因素。通过合理设计谐振频率和品质因数,可制作出具有所需带宽的滤波器,从而有效处理特定频率范围的信号,实现信号的增强或抑制。
低通滤波器
低通滤波器是允许特定频率以下的信号通过,并衰减该频率以上信号的滤波器。RLC电路中的低通滤波器,适用于让低频信号通过。
低通滤波器的工作原理
低通滤波器中,电感器(L)与电容器(C)配合使用。在低频时,电感表现为短路(几乎无电阻),电容表现为开路(电阻无穷大)。凭借这一特性,低频信号可轻松通过滤波器。
计算公式
低通滤波器的截止频率(fC)计算公式如下:
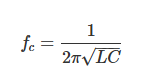
其中,L为电感,C为电容。
滤波器特性
以截止频率为界,低通滤波器的特性发生显著变化。低于该频率的信号几乎无衰减地通过,而高于该频率的信号则急剧衰减。基于这一特性,低通滤波器在电子电路中被用于去除高频噪声。
滤波器的设计与应用
设计低通滤波器时,关键是选择合适的L和C参数,以实现所需的截止频率和频率限制。这类滤波器适用于音频系统、无线电接收机、电力管理系统等多种用途。
低通滤波器通过有效允许低于特定频率的信号通过、阻断高频信号,在减少电子电路中不必要的噪声方面发挥重要作用。通过选择合适的电感器和电容器,可设计出适用特定应用的滤波器。
高通滤波器
高通滤波器是允许高于特定频率的信号通过,并衰减该频率以下信号的滤波器。RLC电路中的高通滤波器,适用于让高频信号通过。
高通滤波器中,电感器(L)与电容器(C)的配置与低通滤波器不同。在高频时,电容表现为短路,电感表现为开路。凭借这一特性,高频信号可轻松通过滤波器。
高通滤波器的计算公式
高通滤波器的截止频率(fc)计算公式如下:
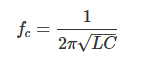
其中,L为电感,C为电容。
滤波器特性
以截止频率为界,高通滤波器的特性发生显著变化。该频率以上的信号几乎无衰减地通过,而低于该频率的信号则急剧衰减。基于这一特性,高通滤波器在电子电路中被用于去除低频噪声。
滤波器的设计与应用
设计高通滤波器时,关键是选择合适的L和C参数,以实现所需的截止频率和频率限制。这类滤波器适用于音频系统、无线通信设备、信号处理系统等多种用途。
高通滤波器允许高于特定频率的信号有效通过、同时阻断低频信号,在减少电子电路中不必要的噪声方面发挥重要作用。通过选择合适的电感和电容,可设计出适用特定场景的滤波器。
带通滤波器
带通滤波器是允许特定频率带宽内的信号通过,并衰减该带宽外信号的滤波器。RLC电路构成的带通滤波器对特定频率范围具有高透过性。
带通滤波器中,电阻(R)、电感(L)、电容(C)以特定方式组合,形成仅允许特定频率带宽通过的结构。在这类滤波器中,谐振频率发挥重要作用。
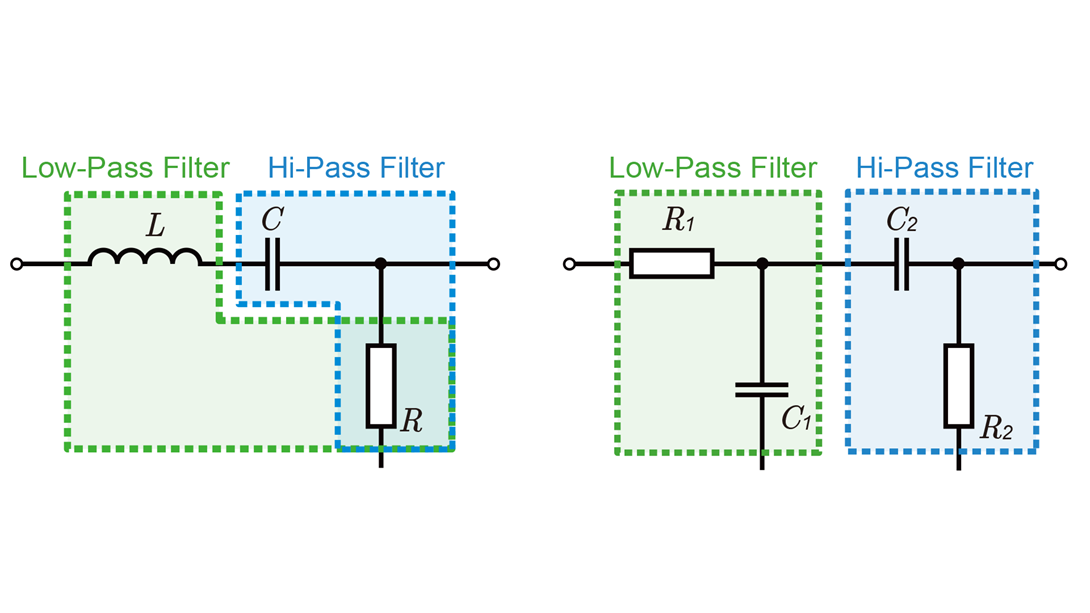
带通滤波器的谐振频率(fr)计算公式如下:
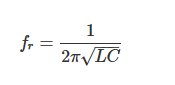
其中,L为电感,C为电容。
滤波器特性
带通滤波器会增强以谐振频率为中心的特定频率范围的信号,并衰减该范围外的信号。基于这一特性,它在通信系统、音频设备等应用中用来提取特定频率的信号。
滤波器的设计与应用
设计带通滤波器时,关键是选择合适的R、L、C参数,以实现所需的谐振频率和带宽。这类滤波器广泛应用于无线通信、音频处理、信号处理系统等领域。
带通滤波器因能增强特定频率带宽的信号并有效衰减其他信号,在众多电子电路中发挥着重要作用。这类滤波器需要根据特定应用进行精密设计。
RLC电路的滤波器应用:缓冲电路
缓冲电路是电力电子领域中用于控制瞬态响应、衰减不必要的电压尖峰和电流尖峰的电路,尤其广泛应用于半导体开关器件(如晶体管、晶闸管)的保护。
缓冲电路通常由电容器(C)和电阻器(R)构成。这些元件以串联或并联方式连接在开关器件的两端。
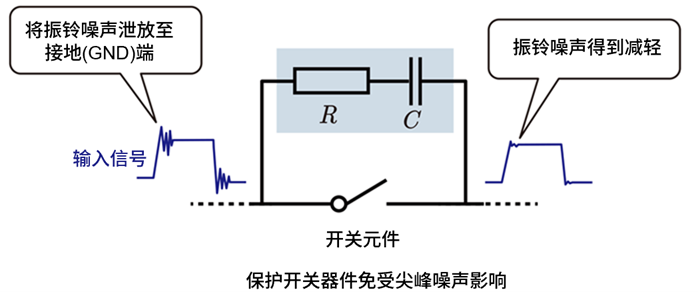
功能与目的
电压尖峰衰减:缓冲电路可抑制开关动作时产生的急剧电压变化。其原理是通过电容器吸收电压尖峰,再由电阻器将吸收的能量转化为热量释放。
电流尖峰管理:电阻器与电容器的组合可衰减流入开关晶体管的急剧电流。
缓冲电路的设计
缓冲电路的设计需基于目标开关器件的特性及使用环境进行,电容器与电阻器的参数值选择需考虑以下因素:
元器件的最大耐压
开关频率
电路的工作环境
计算公式
缓冲电路中电容器(C)与电阻器(R)的参数计算方式如下:
电容值根据器件的瞬态特性选定;
电阻值根据通过电容释放的能量及开关器件的安全工作范围计算。
缓冲电路对延长开关器件的寿命、提高整个系统的可靠性具有重要作用。设计合理的缓冲电路能有效控制瞬态响应,是保护电子器件不可或缺的部分。
RLC电路的滤波器应用:调谐电路
调谐电路是一种为在特定频率下呈现最大或最小响应而设计的电路,其特性广泛应用于无线通信、广播等领域,用于选择性接收特定信号。
调谐电路通常由含电感器(L)和电容器(C)的LC电路构成。该电路在特定谐振频率下发生谐振,相比其他频率具有更强的信号强度。
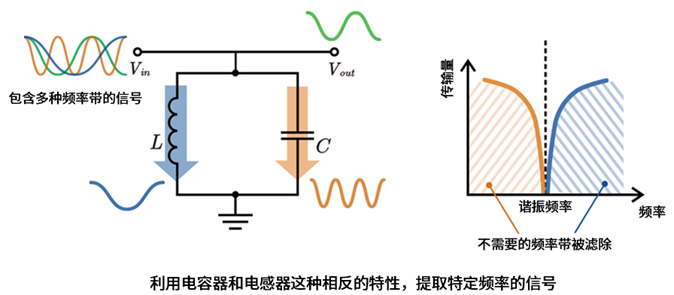
谐振条件
调谐电路的谐振频率f0表达式如下:
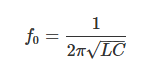
固有频率
谐振频率又称“电路的自由振荡频率(即固有频率)”。在该频率下,电感与电容的电抗相互抵消,电路阻抗达到最小值。
电阻的影响
实际调谐电路中还包含电阻(R),电阻会影响谐振频率下的锐度(Q值),进而决定谐振品质。
Q值的表达式如下:
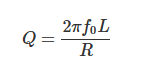
设计要点
选择性:仅对特定频率呈现高响应,排除其他频率的信号;
Q值:高Q值意味着窄带宽,对特定频率的敏感度更高;
应用场景:无线接收机、信号发生器、滤波电路等。
调谐电路凭借其选择性和高Q值,在特定频率的选择性处理中发挥着重要作用。因此,在无线通信系统等应用中,能够高效提取特定信号、排除噪声及其他信号。

 我要赚赏金
我要赚赏金

