EEPW论坛

利用拉普拉斯反变换的定义式（9-1-3），将象函数代入式中进行积分，即可求出相应的原函数，但往往求积分的运算并不简单。下面介绍求反变换的一种校为简便的方法。

设有理分式函数：

若m≥n，则可通过多项式除法得：

式中，整式的拉普拉斯反变换为：

是有理真分式，记为。对于电路问题，多数F(S)是有理真分式即n≥m情况。为求的拉普拉斯反变换，通常利用部分分式展开的方法，将之展开成简单分式之和。简单分式的反变换，可直接查表9-1-1直接获得。

令，求出相应的几个根，记作。根据所求根的不同类型，下面分三种情况进行讨论。

一、当有几个不相同的实数根时

按部分分式展开为：

式中，，……是对应于极点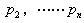的留数。留数可由下面两式求出，即：

（式9-3-1）

或：

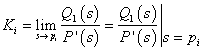（式9-3-2）

于是的反变换式为：

（式9-3-3）

例9-3-1：求的拉普拉斯反变换式。

解：的部分分式展开式为：

由（式9-3-1）：

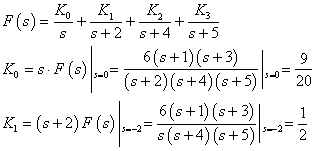
同理可得：，

于是：

二、当包含有共轭复根时

设：

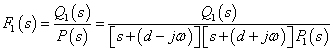
当是实系数多项式时，是复数，是的共轭复数。

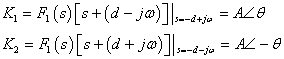
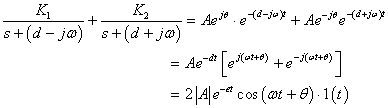
例9-3-2 求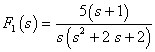的原函数。

解：

由（式9-3-1）：

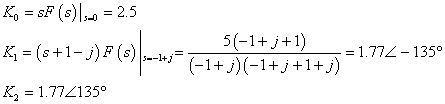
的原函数为：