EEPW论坛

本节介绍拉普拉斯变换（也称为拉氏变换）的基本性质，了解掌握了这些性质，可以更加方便地求解各种拉普拉斯正反变换。

一、线性定理

设 则：

（式9-2-1）

式中为常系数。

例9-2-1 求、和的拉氏变换。

解：

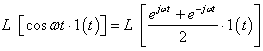
同理：

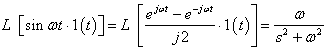
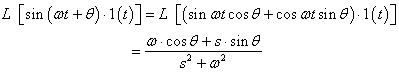
二、微分定理

设 ，则：

（式9-2-1）

同理可推广得到的高阶导数的拉氏变换式：

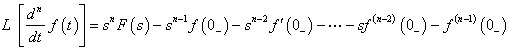
例9-2-2：

已知，求。

解：由于，由（式9-2-2）得：

同理：

三、积分定理

设，则：

（式9-2-3）

例9-2-3 求。

解：斜坡函数是单位阶跃函数的积分，由（式9-2-3）得：

四、时域位移（延时）定理

设，则：

（式9-2-4）

例9-2-4：求图9-2-1所示函数的拉普拉斯变换式。

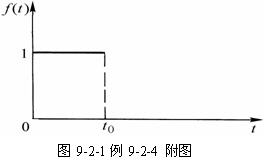
解：由图可知：

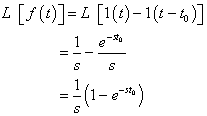
五、复频域位移定理

设，则：

（式9-2-5）

例9-2-5：已知

求：和的拉普拉斯反变换。

解：利用复频域位移定理：

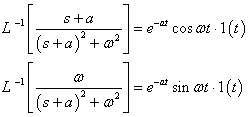
六、卷积定理：

设，则：

（式9-2-6）

例9-2-6．求的拉普拉斯反变换式。

解：已知，利用卷积定理得：

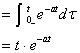
同理可推得：

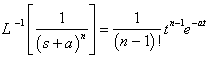
七、初值定理

设，则

例9-2-7．设，验证初值定理。

解：

又：

，所以，得证！

八、终值定理：

设，则

例9-2-8．仍设，验证终值定理。

解：

，又

所以，得证!

注意：利用终值定理求的前提条件是必须存在，且是唯一确定的值。