EEPW论坛

OpenCV-Python系列之图像金字塔

在上一个教程中，我们谈到了关于图像Canny边缘检测算子，同时也是OpenCV中应用最为广泛的边缘检测算法。

现在我们来谈谈图像金字塔，它的本质是对图像进行放缩变换。一般情况下，我们要处理是一副具有固定分辨率的图像。但是有些情况下，我们需要对同一图像的不同分辨率的子图像进行处理。比如，我们要在一幅图像中查找某个目标，比如脸，我们不知道目标在图像中的尺寸大小。这种情况下，我们需要创建一组图像，这些图像是具有不同分辨率的原始图像。我们把这组图像叫做图像金字塔（简单来说就是同一图像的不同分辨率的子图集合）。如果我们把最大的图像放在底部，最小的放在顶部，看起来像一座金字塔，故而得名图像金字塔。

图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。

有两类图像金字塔：高斯金字塔和拉普拉斯金字塔：

高斯金字塔(Gaussianpyramid): 用来向下采样，主要的图像金字塔

拉普拉斯金字塔(Laplacianpyramid): 用来从金字塔低层图像重建上层未采样图像，在数字图像处理中也即是预测残差，可以对图像进行最大程度的还原，配合高斯金字塔一起使用。

两者的简要区别：高斯金字塔用来向下降采样图像，而拉普拉斯金字塔则用来从金字塔底层图像中向上采样重建一个图像。要从金字塔第i层生成第i+1层（我们表示第i+1层为G_i+1），我们先要用高斯核对G_1进行卷积，然后删除所有偶数行和偶数列。当然的是，新得到图像面积会变为源图像的四分之一。按上述过程对输入图像G_0执行操作就可产生出整个金字塔。

　　当图像向金字塔的上层移动时，尺寸和分辨率就降低。OpenCV中，从金字塔中上一级图像生成下一级图像的可以用PryDown。而通过PryUp将现有的图像在每个维度都放大两遍。

图像金字塔中的向上和向下采样分别通过OpenCV函数 pyrUp 和 pyrDown 实现。

对图像向上采样：pyrUp函数

对图像向下采样：pyrDown函数

这里的向下与向上采样，是对图像的尺寸而言的（和金字塔的方向相反），向上就是图像尺寸加倍，向下就是图像尺寸减半。而如果我们按上图中演示的金字塔方向来理解，金字塔向上图像其实在缩小，这样刚好是反过来了。

但需要注意的是，PryUp和PryDown不是互逆的，即PryUp不是降采样的逆操作。这种情况下，图像首先在每个维度上扩大为原来的两倍，新增的行（偶数行）以0填充。然后给指定的滤波器进行卷积（实际上是一个在每个维度都扩大为原来两倍的过滤器）去估计“丢失”像素的近似值。

PryDown( )是一个会丢失信息的函数。为了恢复原来更高的分辨率的图像，我们要获得由降采样操作丢失的信息，这些数据就和拉普拉斯金字塔有关系了。

高斯金字塔

高斯金字塔是通过高斯平滑和亚采样获得一些列下采样图像，也就是说第K层高斯金字塔通过平滑、亚采样就可以获得K+1层高斯图像，高斯金字塔包含了一系列低通滤波器，其截至频率从上一层到下一层是以因子2逐渐增加，所以高斯金字塔可以跨越很大的频率范围。金字塔的图像如下：

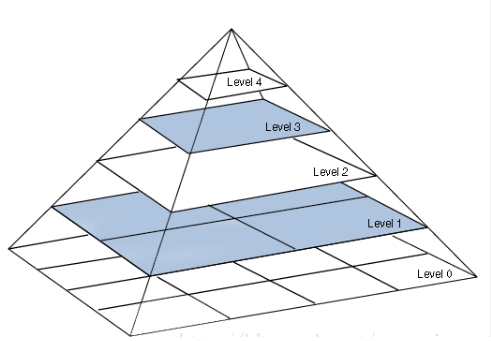
另外，每一层都按从下到上的次序编号，层级 G_i+1 (表示为 G_i+1尺寸小于第i层G_i)。

（1）对图像的向下取样

为了获取层级为 G_i+1 的金字塔图像，我们采用如下方法:

1、对图像G_i进行高斯内核卷积

2、将所有偶数行和列去除

得到的图像即为G_i+1的图像，显而易见，结果图像只有原图的四分之一。通过对输入图像G_i(原始图像)不停迭代以上步骤就会得到整个金字塔。同时我们也可以看到，向下取样会逐渐丢失图像的信息。以上就是对图像的向下取样操作，即缩小图像。

我们来看函数原型：

cv2. pyrDown (src, dst=None, dstsize=None, borderType=None)

参数含义：

src：表示输入图像

dst：表示输出图像

dstsize：表示输出图像的大小

borderType：表示图像边界的处理方式

我们来看源代码：

import cv2
import numpy as np

img = cv2.imread("cat.jpg")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
dst = cv2.pyrDown(img)
cv2.imshow("img",img)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()

（2）对图像的向上取样

同样的，我们来看函数原型：

cv2. pyrUp (src, dst=None, dstsize=None, borderType=None)

参数含义：

src：表示输入图像

dst：表示输出图像

dstsize：表示输出图像的大小

borderType：表示图像边界的处理方式

直接来看代码：

import cv2
import numpy as np

img = cv2.imread("cat.jpg")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
dst = cv2.pyrUp(img)
cv2.imshow("img",img)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()

具体的效果大家可以自己实验。

拉普拉斯金字塔

与其说是拉普拉斯金字塔，不如叫做残差金字塔。因为我们刚刚不是说了吗，图像的降采样和上采样不是可逆的。那么拉普拉斯金字塔的构建方法如下：

假设高斯金字塔就 3 个 level（0， 1，2），那么，我们先把高斯金字塔的最高层（最小的那个）上采样（放大）。我们知道，上采样之后和原金字塔第 1 个 level相比是有信息丢失的，我们就把原高斯金字塔的第 1 个level 的图像和这个经过 第 2 个level 图像上采样得到的图像相减（第 2 个 level 图像上采样之后就和原高斯金字塔第 1 个 level 图像的大小一样了），相减就会得到一个残差，这就是拉普拉斯金字塔的最高级（下图中就应该是 level 1）。

同样地，把原高斯金字塔的 level 0 的图像 和 原高斯金字塔 level 1 经过上采样得到的图像相减，就得到了拉普拉斯金字塔的第 0 层。至此，下图所示的拉普拉斯金字塔就构建完毕了。

值得注意的是：如果一幅图像的高斯金字塔有 N+1 层，那么其对应的拉普拉斯金字塔就有 N 层。

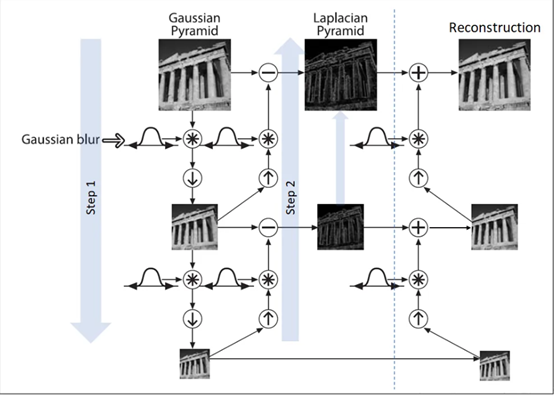
拉普拉斯金字塔的整个计算过程如上图所示：

1.左上角的图片为原始图片

2.对原始图像进行高斯平滑

3.执行一次下采样，图像变为原来的1/4

4.执行一次上采样，图像变为原图的大小

5.再次执行高斯模糊

6.用原图像减去高斯模糊后的图像，得到拉普拉斯图像

我们来看代码实战：

import cv2
import numpy as np

img = cv2.imread("cat.jpg")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
down = cv2.pyrDown(img)
dst = cv2.pyrUp(down)
res = img - dst
cv2.imshow("img",img)
cv2.imshow("res",res)

cv2.waitKey(0)
cv2.destroyAllWindows()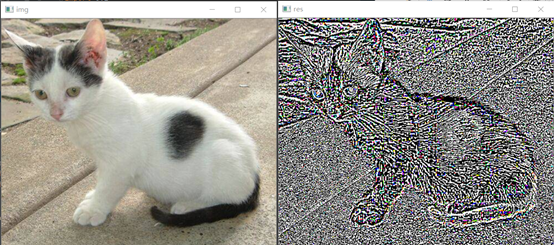

图像金字塔实际上是有着很大的用途的，包括图像融合，但这些我们将在后面的项目实战中介绍到。