EEPW论坛

OpenCV-Python系列之单应性查找对象理论篇

注意：本教程中将涉及到机器学习的一些概念，但不进行过多的详述。

我们在上一个教程中所提及到的FLANN算法就属于单应性算法，先解释一下单应性，在计算机视觉中：平面的单应性被定义为从一个平面到另一个平面的投影映射。比如，一个二维平面上的点映射到摄像机成像仪上的映射就是平面单应性的例子。

之前我们使用一个查询图像，在其中找到一些 特征点（关键点），我们又在另一幅图像中也找到了一些特征点，最后对这两幅 图像之间的特征点进行匹配。简单来说就是：我们在一张杂乱的图像中找到了 一个对象（的某些部分）的位置。这些信息足以帮助我们在目标图像中准确的 找到（查询图像）对象。

为了达到这个目的我们可以使用calib3d模块中的cv2.findHomography()函数。如果将这两幅图像中的特征点集传给这个函数，他就会找到这个对象的****图变换。然后我们就可以使用函数 cv2.perspectiveTransform() 找到这个对象了，至少要 4 个正确的点才能找到这种变换。

我们已经知道在匹配过程可能会有一些错误，而这些错误会影响最终结果。为了解决这个问题，算法使用 最小二乘法、RANSAC 、 LMEDS及PROSAC(可以通过参数来设定)。所以好的匹配提供的正确的估计被称为 inliers，剩下的被称为 outliers。cv2.findHomography() 返回一个掩模，这个掩模确定了 inlier 和 outlier 点。

接下来我们将介绍四个相关算法，本次教程只介绍前两个。

最小二乘法

我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？ 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面。

对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
      2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
       3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

最常用的是普通最小二乘法：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和），即采用平方损失函数。

样本回归模型：

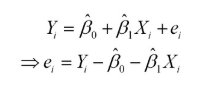
其中ei为样本（Xi, Yi）的误差。

   平方损失函数：

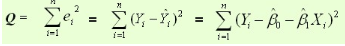
则通过Q最小确定这条直线，即确定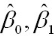，以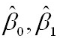为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数：

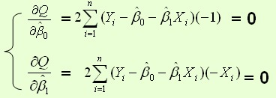
根据数学知识我们知道，函数的极值点为偏导为0的点。

解得：

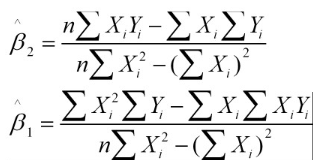
这就是最小二乘法的解法，就是求得平方损失函数的极值点。

RANSAC算法

通俗的来讲，普通最小二乘是保守派：在现有数据下，如何实现最优。是从一个整体误差最小的角度去考虑，尽量谁也不得罪。

RANSAC是改革派：首先假设数据具有某种特性（目的），为了达到目的，适当割舍一些现有的数据。

给出最小二乘拟合（红线）、RANSAC（绿线）对于一阶直线、二阶曲线的拟合对比：

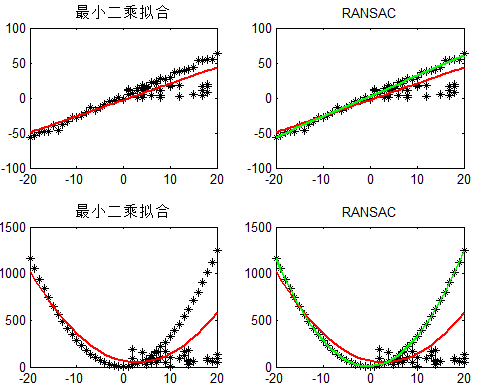
可以看到RANSAC可以很好的拟合。RANSAC可以理解为一种采样的方式，所以对于多项式拟合、混合高斯模型（GMM）等理论上都是适用的。

RANSAC简化版的思路就是：

第一步：假定模型（如直线方程），并随机抽取Nums个（以2个为例）样本点，对模型进行拟合：

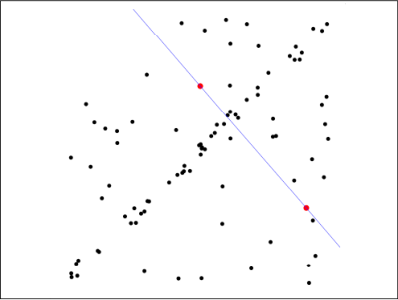
第二步：由于不是严格线性，数据点都有一定波动，假设容差范围为：sigma，找出距离拟合曲线容差范围内的点，并统计点的个数：

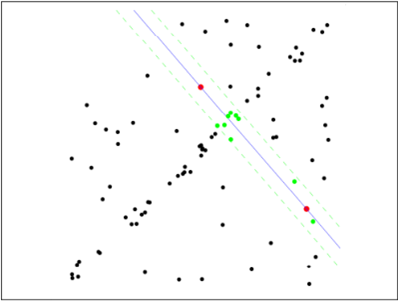
第三步：重新随机选取Nums个点，重复第一步~第二步的操作，直到结束迭代：

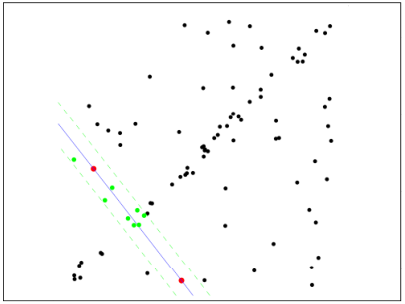
第四步：每一次拟合后，容差范围内都有对应的数据点数，找出数据点个数最多的情况，就是最终的拟合结果：

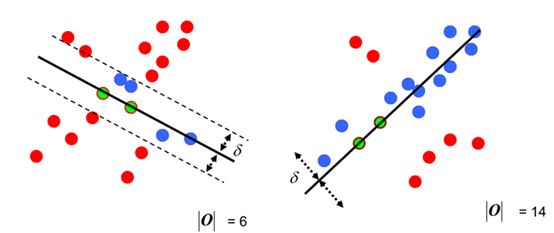
至此：完成了RANSAC的简化版求解。

事实上，以上这些思想属于机器学习的思想，现在只是简述，机器学习属于相当复杂的学科门类，现在不多进行赘述。

我们本次教程只介绍前两个算法，下次我们介绍另外两个算法，它们都属于机器学习的相关范畴。