EEPW论坛

一个电感和一个电容串联，在某个特定的频率，就会发生谐振，这个频率就是谐振频率。串联谐振电路有如下特点：

谐振时整个电路阻抗呈电阻性，阻抗最小，电流达到最大；

谐振时电感和电容两端的电压达到最大。

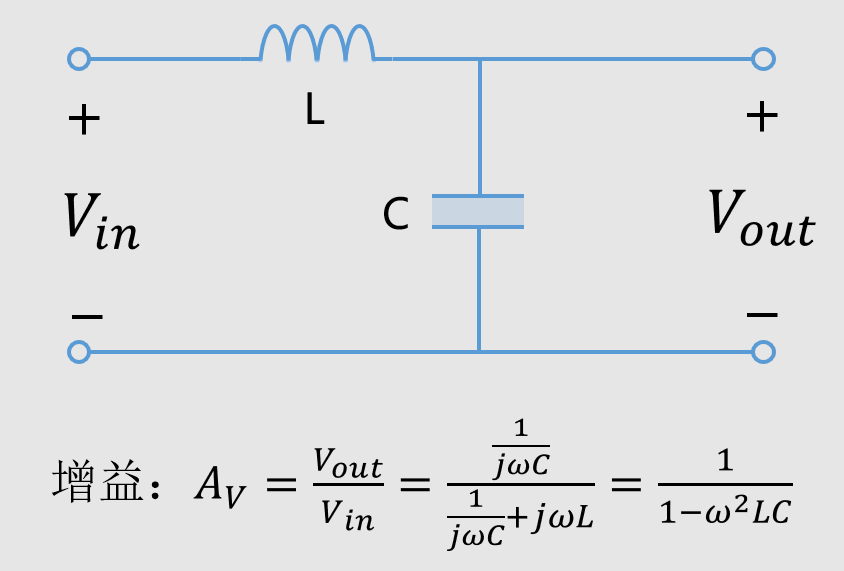
上图就是一个LC串联典型电路，一般被用于低通滤波。我们准备一个电感和电阻串联的电路如下所示：

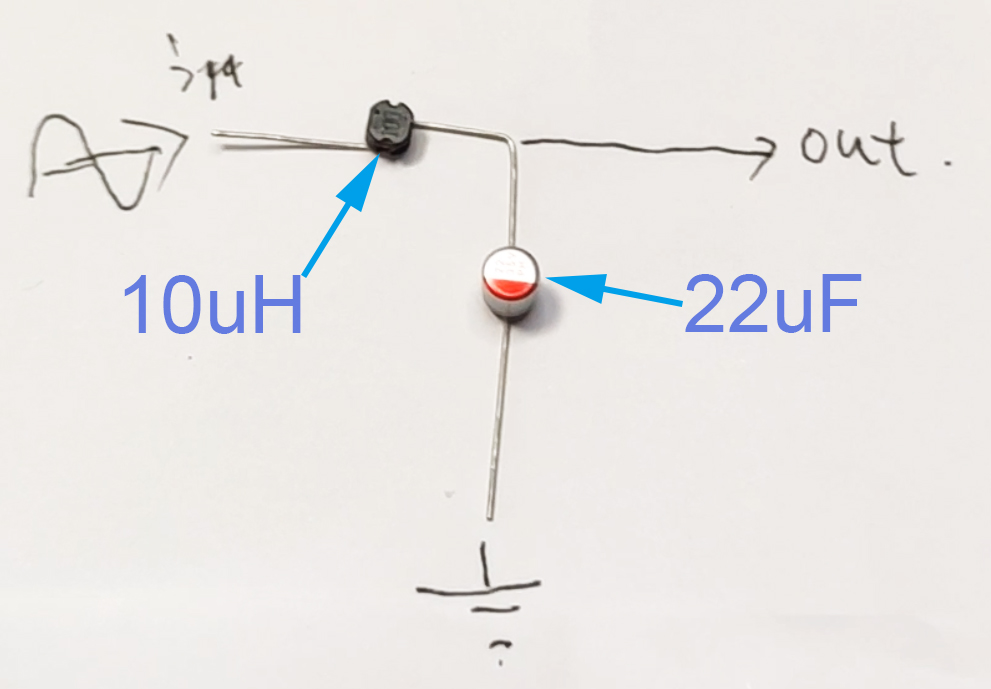
我们准备一台LOTO的虚拟示波器OSCH02S，也就是示波器加信号源的版本，我们用信号源产生一个扫频正弦波，作为上图的Vin输入，把示波器的AB两个通道加在输入Vin和输出端Vout处。

我们在上位机软件上设置好扫频参数，如下图所示：

我们先扫频得到通道A也就是输入端的频响曲线如下图所示，可以看到扫频正弦波信号加在LC串联电路两端，示波器CHA也就是LC两端的信号幅频曲线中，一开始幅值比较大，随着频率的升高，信号幅值逐渐变小，最小的位置，也就是截止频率处，我们看到图中的光标测量出来是183.51K赫兹。过了这个截止频率，信号的幅值又逐渐变大起来。截止频率附近的信号幅值变小是因为产生谐振的时候LC的整体阻抗最小，这时候它所分得的信号也就是最小。

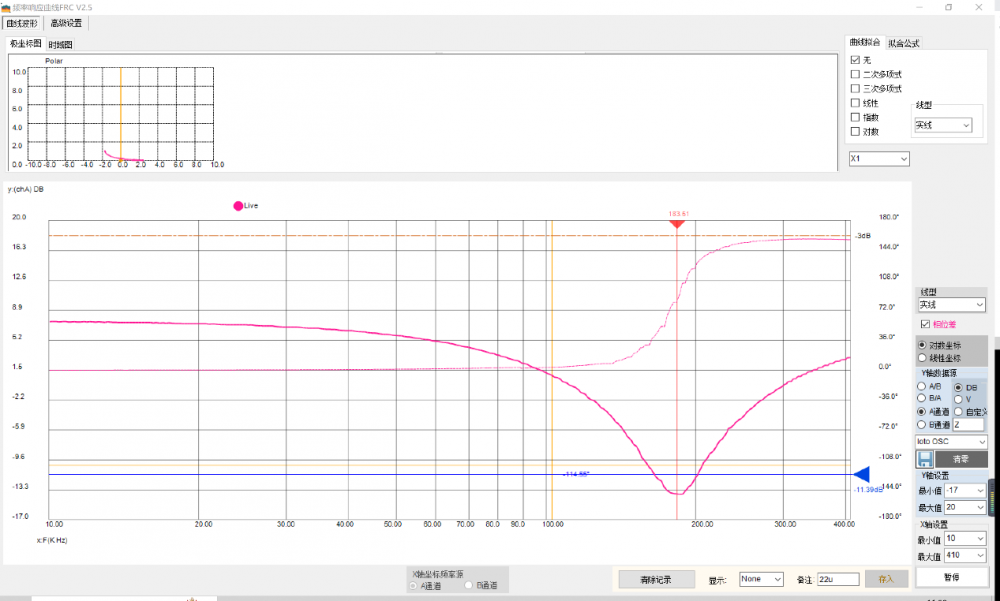
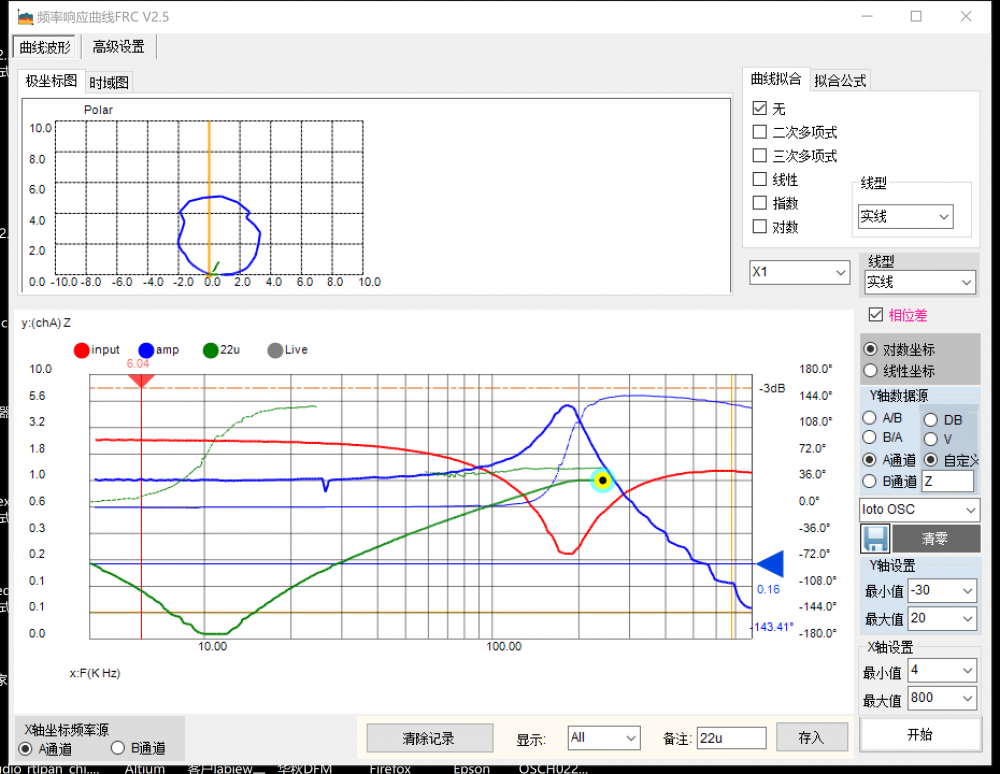
我们这次来测增益曲线，也就是Vout/Vin的频响曲线，我们只需要在频响曲线界面把Y周的数据来源从chA改为B/A就可以了，重新扫频，得到如下的幅频曲线：

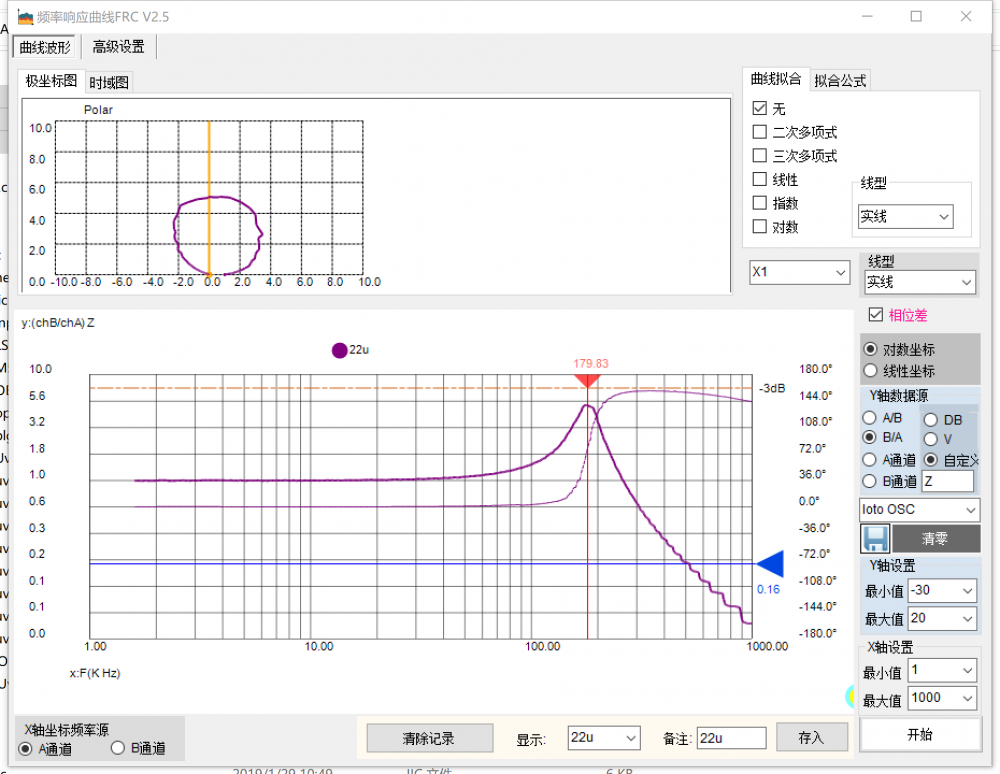
这个增益曲线，我们也可以理解成是低通滤波器的增益曲线。前一段可以看出增益为1，相位差也为0，也就是输出=输入。到谐振频率附近，放大倍数大概6倍左右，也就是这时候的信号被放大了，之后放大倍数迅速减小。

如果我们能把谐振频率处的增益降到0.707左右，那就是完美的低通滤波器了。很显然，电感和电容都是非耗能器件，没有电阻器件的引入，在谐振频率处，增益总是很大。

幸运的是，我们的滤波电路总是要接负载的，我们把信号滤波之后总是要给负载用的，接入了负载，那增益又不一样了。负载越大，这个谐振点的增益会越小。

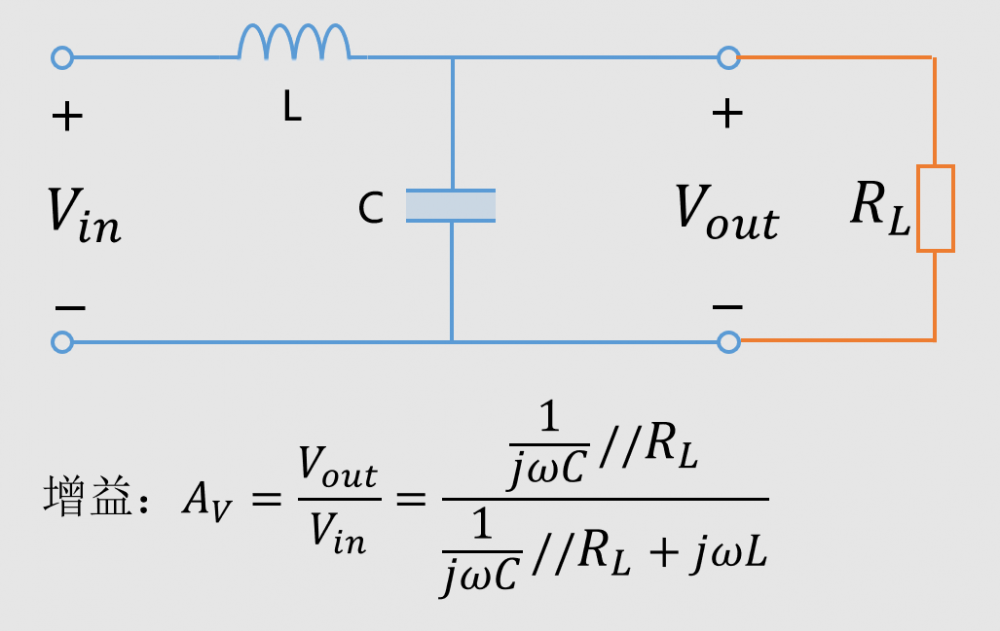
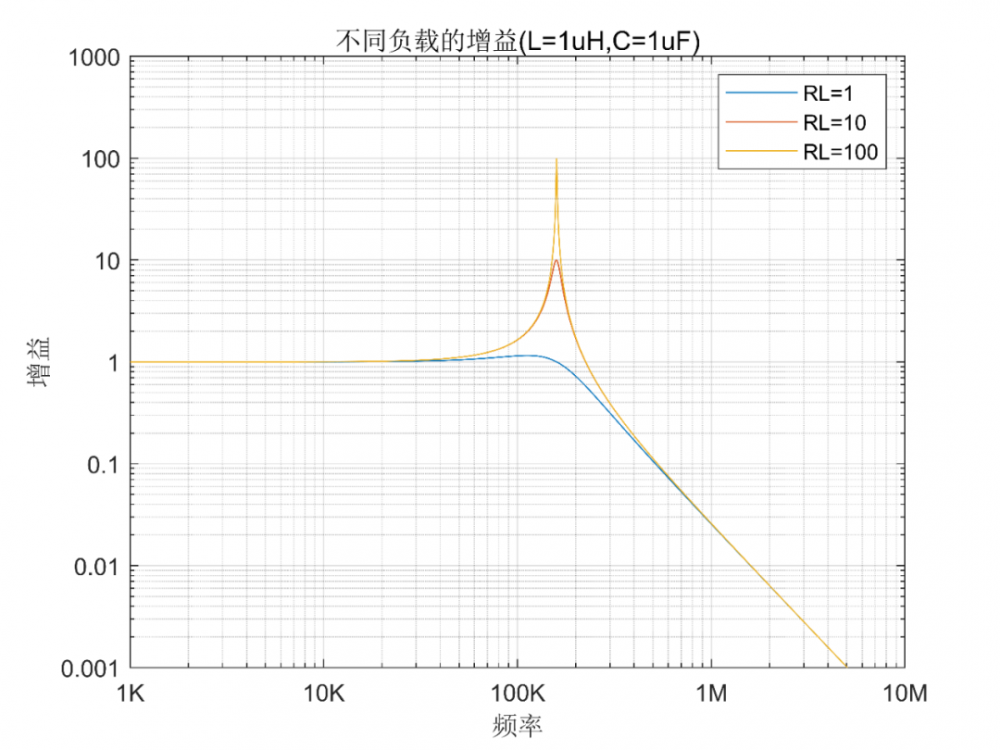
我们可以看到，负载电阻越小，谐振处的增益越小，谐振引起的噪声变大越不会发生。当然了，实际电路中的负载各种各样，有低阻的，有高阻的。相对来说，低阻负载的更不容易发生加入滤波器效果更差的事情。因此，如果你发现同样的LC滤波器，加入不同的电路，有的效果好，有的效果变差，很有可能就是因为负载的不同。

所以说，负载阻抗越低，越不容易产生尖峰，也就是说不容易恶化。

不同的LC参数也会有不同的谐振频率的情况。我们改变一些参数可以测的不同的频响曲线如下：

整个过程我们制作了视频演示，可以参看如下：

《LOTO示波器LC串联谐振测试 实测演示 -- LC滤波/频响曲线/频率谐振点》

https://www.bilibili.com/video/BV1HN411n7mS/?spm_id_from=333.999.0.0&vd_source=c0bedc6c664e75d3c19935cbda8abe19