引言
Maxim的iButton系列产品是通过单线按照1-Wire协议传送特定命令序列,进行数据通信。该系列产品都有个很重要的特性,就是在出厂前每个器件都被写入了唯一的8字节ROM码。其ROM码组成如图1所示,最低有效字节为家族代码,代表iButton器件的类型,如:DS1990A的家族码为01,DS1991的家族码为02。由于在同一条1-Wire总线上可同时挂接多个相同系列或不同系列的1-Wire器件,因此主机必须能够决定如何正确地访问位于1-Wire总线上的各个器件,这一点尤为重要。家族码提供器件的类型,随后的6个字节是器件的唯一序列号,用以区分同一个系列的不同器件。该序列号可作为1-Wire总线上器件的“地址”,这样1-Wire总线上的所有器件连同主机就构成了一个微型局域网(MicroLAN),它们之间通过一条公共线来进行通信。1-Wire器件ROM码的最高有效字节是循环冗余校验(CRC)码,该值基于前面的7个字节数据。当系统主机开始与某个器件进行通信时,可以读取8个ROM字节,低位在前。如果主机计算出的CRC码与ROM数据本身所含的CRC码相同,则通信有效;反之,则表明有错误发生,需重新读取器件的ROM码。
图1. 采用DOW CRC的iButton系统配置
有些iButton器件除了8字节ROM外,还具有高达8kB的RAM,主机可以通过适当的命令进行访问。即使iButton器件本身不带CRC硬件电路,如果主机具有为ROM码计算CRC值的能力,就可以采用CRC技术,开发一个访问器件RAM部分的子程序。数据按正常模式写入器件,主机将计算出的CRC结果附在数据后面,与数据一起保存。当从iButton器件读入数据时,则执行相反的过程。主机将计算出的CRC值与存储器中存储的CRC进行比较,如果相同,则认为从iButton接收的数据有效。为了充分利用CRC来验证1-Wire总线上进行的串行通信的有效性,用户有必要了解一下CRC的概念和工作原理。此外,无论是基于硬件实现还是软件实现,还需要掌握通过主机计算CRC的实用计算方法。
有多种串行数据的检错方法,一种常用的方法是在被检测的数据包中包含一个附加位,用于指示是否出错。如:对于8位ASCII字符来说,可在其ASCII字符串后添加一位用于检错。假设数据为11010001,可以附加第9位,使数据中"1"的位数为奇数个。这样,应该附加1,数据包就变为:111010001,其中带下划线的字符为所要求的奇偶校验位,使全部9位数据中1的位数为奇数。如果收到的数据为:111010001,则认为接收到的信息有效;但是,若收到的数据为:111010101,即左边第七位接收错误,此时数据中"1"的个数就不再是奇数,则表明发生了错误,进而采取相应的措施,这种校验方法称作奇校验。与之类似,如果要求数据中1的个数总为偶数,则称为偶检验。但是这种检验方式有其局限性,它只能检查出数据中的奇数个错误。在上例中,如果收到的数据为:111011101,其中从左边数第6位和第7位都是错的,但此时奇偶检测结果却是正确的。对于这类错误,因此无论采用奇校验还是偶校验,都不能够检测出来。
详述 Maxim 1-Wire器件的CRC在串行数据流中发现错误的最有效检错方案是循环冗余校验(CRC),并且所要求的硬件最少。这里主要介绍Maxim器件的CRC校验的工作及特性,暂不涉及详细的数学定义和描述。包含在CRC特性之后的数学概念在参考资料中进行了详细介绍。由于CRC实际上是由硬件实现,因此很容易理解CRC功能,通常CRC表示为带反馈的移位寄存器,如图2所示。另一种方式,也可将CRC看成是变量X的多项式,每一项的系数为二进制数,这些系数与移位寄存器的反馈通道直接对应。硬件方案中的移位寄存器的阶数,或多项式中的最高幂次就是将要计算CRC的位数。通常数字通信中使用的CRC编码方式有CRC-16和CRC-CCITT,它们产生的CRC码都为16位。Maxim的1-Wire CRC (DOW CRC)的位数是8位,用于1-Wire器件的64位ROM码的检错,该ROM码包括:最低有效字部分的8位家族码、与最低有效字节紧挨着的6字节48位唯一序列号、位于最高有效字节是前56位ROM码所计算出的CRC校验码。图2中,异或门构成的反馈路径(多项式的系数)决定了CRC检错性能和错误定位性能。DOW CRC可检测到以下几种错误:
- 任意64位数据中的奇数个错误。
- 所有64位数据中的双位错误。
- 包含在8位"window" (1至8位错误)中的任何字符串的错误。
- 绝大多数长字符串的错误。
如图2所示,输入数据是与移位寄存器的第8阶输出进行异或,移位寄存器在数学上可被视为除法电路,其中输入数据为被除数,反馈移位寄存器为除数,计算所得的商数在这里没有价值,计算后的余数就是指定数据流的CRC码。当最后一位数据移入之后,移位寄存器的值就是最后的余数。通过用移位寄存器来实现CRC的方案不难看出,最后得到的结果(CRC码)是根据要发送的所有数据,通过一种非常复杂的过程获得的,故此,这种校验算法基本上可以检测出数据中大多数的错误,只有极少数特别极端情况的差错无法检测到。
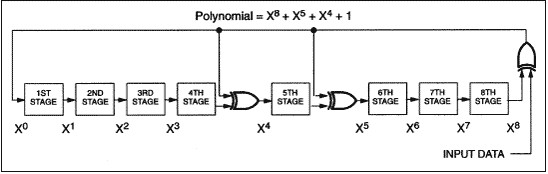
图2. Maxim 1-Wire 8位CRC
例2所示是当所有数据都移入之后计算出的CRC码。在计算开始时移位寄存器全置为‘0’,计算由64位ROM的LSB位开始,本例中家族码为02。当56位数据(序列号加上家族码)都移入后,移位寄存器的的值变为A2,这就是输入数据流的DOW CRC码。如果把计算得到的CRC码(A2)的8个位接在数据流的后面继续移入移位寄存器,那么当64位数据全部输入后,移位寄存器的值就全部为0。在DOW CRC算法中,就是利用这样一个特性来检查是否发生了错误的。把任意的8位数据移入移位寄存器到得到的8位数字接在移入的数据的后面继续移入移位寄存器,那么第8位数据位移入后的移位寄存器的结果总为00,通过观察不难注意到,移位寄存器的第8阶的值总是和输入的数据位相等,这样就使得用来控制反馈的异或门的输出和移位寄存器第一阶的下一个状态总为逻辑0,这样一来,当数据移入时,从左到右移入的每一位都是0,直到第8位后移位寄存器的每一位都被置0为止。Maxim 1-Wire 64位ROM就是利用上述特性来简化64位ROM的硬件设计的。主机端的移位寄存器首先被清0,然后读取包括CRC码在内的64位ROM。如果读取正确,则移位寄存器为零,易于检测。如果移位寄存器的值不是全部为0,则(表示发生了错误)必须重新读取数据。
到现在为止,我们一直围绕CRC硬件实现方法进行讨论,当然,与硬件方法等价的软件解决方案,则是另一种计算DOW CRC码的实现方法。如何编写程序代码如例1示例所示。需注意的是,寄存器A与常量18的异或运算是为了实现DOW CRC中第4、5阶之后的的异或反馈门,如图2所示。另一种软件实现方案就是简单地构建一个查询表,可以根据CRC寄存器中的8位值和新的8位数据直接读取。对于CRC寄存器为00的这种简单情况,可以推出输入数据的256种不同的组合,并将它们保存距阵中,该距阵索引值等于输入数据(即索引值为:I = 0至255)。很明显,如果CRC寄存器的当前值不是00,那么对于任一个当前CRC码和输入字来说,其查询表的值与CRC寄存器为0的简单情况相同,但表的索引值计算方式应改为:
新CRC = 表[I],I = 0至255 ;
这里,I = (当前CRC) EXOR (输入字)。
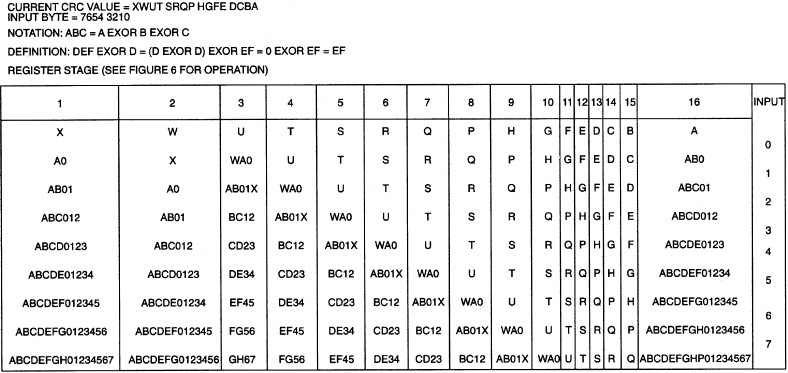
当CRC寄存器的当前值为00时,该等式就和上述简单情况一样。由于第二种方案是以字节为基础进行操作,而不是上例中面向位的操作,因此可以节省计算时间。但该方法会占用存储器的空间,因为查询表是存储在存储器中的,占用256字节,而在第一种方案中除了程序代码外,不再需要占用任何存储空间。例3为第二种方案的程序代码示例,表1给出了上例中查询表实现方法。在生成CRC码时,DOW CRC的两个特性有助于其代码的调试,其中的第一个特性在硬件实现时已介绍过,即:如果下一个输入数据等于当前CRC寄存器值,则计算后的CRC码肯定为00 (见前面的说明)。其第二个特性也能够用于确认代码是否正确,出现在输入数据等于当前CRC寄存器的反码时。对于DOW CRC算法来说,计算出的CRC码将为35H,即十进制的53 。当输入数据为CRC寄存器反码时,通过观察CRC寄存器工作方式,就可以解释这种特性,如表2所示。
DO_CRC: PUSH ACC ;save accumulator PUSH B ;save the B register PUSH ACC ;save bits to be shifted MOV B,#8 ;set shift = 8 bits ; CRC_LOOP: XRL A,CRC ;calculate CRC RRC A ;move it to the carry MOV A,CRC ;get the last CRC value JNC ZERO ;skip if data = 0 XRL A,#18H ;update the CRC value ; ZERO: RRC A ;position the new CRC MOV CRC,A ;store the new CRC POP ACC ;get the remaining bits RR A ;position the next bit PUSH ACC ;save the remaining bits DJNZ B,CRC_LOOP ;repeat for eight bits POP ACC ;clean up the stack POP B ;restore the B register POP ACC ;restore the accumulator RET例2. DOW CRC算法举例
| CRC Value | Input Value |
| 00000000 | 0 |
| 00000000 | 1 |
| 10001100 | 0 2 |
| 01000110 | 0 |
| 00100011 | 0 |
| 10011101 | 0 |
| 11000010 | 0 0 |
| 01100001 | 0 |
| 10111100 | 0 |
| 01011110 | 0 |
| 00101111 | 1 C |
| 00010111 | 1 |
| 00001011 | 1 |
| 00000101 | 0 |
| 10001110 | 0 1 |
| 01000111 | 0 |
| 10101111 | 0 |
| 11011011 | 0 |
| 11100001 | 0 8 |
| 11111100 | 1 |
| 11110010 | 1 |
| 11110101 | 1 |
| 01111010 | 0 B |
| 00111101 | 1 |
| 00011110 | 1 |
| 10000011 | 0 |
| 11001101 | 0 1 |
| 11101010 | 0 |
| 01110101 | 0 |
| 10110110 | 0 |
| 01011011 | 0 0 |
| 10100001 | 0 |
| 11011100 | 0 |
| 01101110 | 0 |
| 00110111 | 0 0 |
| 10010111 | 0 |
| 11000111 | 0 |
| 11101111 | 0 |
| 11111011 | 0 0 |
| 11110001 | 0 |
| 11110100 | 0 |
| 01111010 | 0 |
| 00111101 | 0 0 |
| 10010010 | 0 |
| 01001001 | 0 |
| 10101000 | 0 |
| 01010100 | 0 0 |
| 00101010 | 0 |
| 00010101 | 0 |
| 10000110 | 0 |
| 01000111 | 0 0 |
| 10101101 | 0 |
| 11011010 | 0 |
| 01101101 | 0 |
| 10111010 | 0 0 |
| 01011101 | 0 |
| 10100010 = A2 Hex = CRC Value for [00000001B81C (Serial Number) + 02 (Family Code)] | |
| 10100010 | 0 |
| 01010001 | 1 |
| 00101000 | 0 2 |
| 00010100 | 0 |
| 00001010 | 0 |
| 00000101 | 1 |
| 00000010 | 0 A |
| 00000001 | 1 |
| 00000000 = 00 Hex = CRC Value for A2 [(CRC) + 00000001B81C (Serial Number) + 02 (Family Code)] |
例3. DOW CRC查询函数
Var
CRC : Byte;
Procedure Do_CRC(X: Byte);
{
This procedure calculates the cumulative Maxim 1-Wire CRC of all bytes passed to it.
The result accumulates in the global variable CRC.
}
Const
Table : Array[0..255] of Byte = (
0, 94, 188, 226, 97, 63, 221, 131, 194, 156, 126, 32, 163, 253, 31, 65,
157, 195, 33, 127, 252, 162, 64, 30, 95, 1, 227, 189, 62, 96, 130, 220,
35, 125, 159, 193, 66, 28, 254, 160, 225, 191, 93, 3, 128, 222, 60, 98,
190, 224, 2, 92, 223, 129, 99, 61, 124, 34, 192, 158, 29, 67, 161, 255,
70, 24, 250, 164, 39, 121, 155, 197, 132, 218, 56, 102, 229, 187, 89, 7,
219, 133, 103, 57, 186, 228, 6, 88, 25, 71, 165, 251, 120, 38, 196, 154,
101, 59, 217, 135, 4, 90, 184, 230, 167, 249, 27, 69, 198, 152, 122, 36,
248, 166, 68, 26, 153, 199, 37, 123, 58, 100, 134, 216, 91, 5, 231, 185,
140, 210, 48, 110, 237, 179, 81, 15, 78, 16, 242, 172, 47, 113, 147, 205,
17, 79, 173, 243, 112, 46, 204, 146, 211, 141, 111, 49, 178, 236, 14, 80,
175, 241, 19, 77, 206, 144, 114, 44, 109, 51, 209, 143, 12, 82, 176, 238,
50, 108, 142, 208, 83, 13, 239, 177, 240, 174, 76, 18, 145, 207, 45, 115,
202, 148, 118, 40, 171, 245, 23, 73, 8, 86, 180, 234, 105, 55, 213, 139,
87, 9, 235, 181, 54, 104, 138, 212, 149, 203, 41, 119, 244, 170, 72, 22,
233, 183, 85, 11, 136, 214, 52, 106, 43, 117, 151, 201, 74, 20, 246, 168,
116, 42, 200, 150, 21, 75, 169, 247, 182, 232, 10, 84, 215, 137, 107, 53);
Begin
CRC := Table[CRC xor X];
End;
表1. 查表方式计算DOW CRC
| Current CRC Value (= Current Table Index) | Input Data | New Index (= Current CRC xor Input Data) | Table (New Index) (= New CRC Value) |
| 0000 0000 = 00 Hex | 0000 0010 = 02 Hex | (00 H xor 02 H) = 02 Hex = 2 Dec | Table[2]= 1011 1100 = BC Hex = 188 Dec |
| 1011 1100 = BC Hex | 0001 1100 = 1C Hex | (BC H xor 1C H) = A0 Hex = 160 Dec | Table[160]= 1010 1111 = AF Hex = 175 Dec |
| 1010 1111 = AF Hex | 1011 1000 = B8 Hex | (AF H xor B8 H) = 17 Hex = 23 Dec | Table[23]= 0001 1110 = 1E Hex = 30 Dec |
| 0001 1110 = 1E Hex | 0000 0001 = 01 Hex | (1E H xor 01 H) = 1 F Hex = 31 Dec | Table[31]= 1101 110 = DC Hex = 220 Dec |
| 1101 1100 = DC Hex | 0000 0000 = 00 Hex | (DC H xor 00 H) = DC Hex = 220 Dec | Table[220]= 1111 0100 = F4 Hex = 244 Dec |
| 11110100 = F4 Hex | 0000 0000 = 00 Hex | (F4 H xor 00 H) = F4 Hex = 244 Dec | Table [244]= 0001 0101 = 15 Hex = 21 Dec |
| 0001 0101 = 15 Hex | 0000 0000 = 00 Hex | (15 H xor 00 H) = 15 Hex = 21 Dec | Table[21]= 1010 0010 = A2 Hex = 162 Dec |
| 1010 0010 = A2 Hex | 10100010 = A2 Hex | (A2 H xor A2 H) = Hex = 0 Dec | Table[0]=0000 0000 = 00 Hex = 0 Dec |
表2. CRC寄存器值输入
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X7* |
| 1 | X0 | X1 | X2 | X3* | X4* | X5 | X6 | X6* |
| 1 | 1 | X0 | X1 | X2* | X3 | X4* | X5 | X5* |
| 1 | 1 | 1 | X0 | X1* | X2* | X3 | X4* | X4* |
| 0 | 1 | 1 | 1 | X0 | X1* | X2 | X3 | X3* |
| 1 | 0 | 1 | 1 | 0 | X0* | X1* | X2 | X2* |
| 1 | 1 | 0 | 1 | 0 | 1 | X0* | X1* | X1* |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | X0* | X0* |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | Final CRC Value = 35 Hex, 53 Decimal |



 我要赚赏金
我要赚赏金

