EEPW论坛

这篇文章来源于DevicePlus.com英语网站的翻译稿。

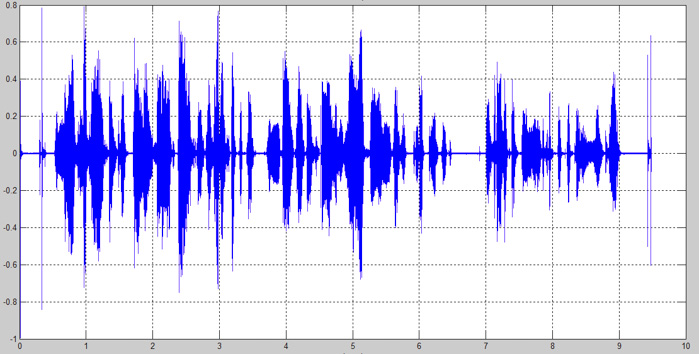
在本教程中，我们将分析语音信号。我们人类发出的声波是连续的模拟信号，然而对于信号处理，我们需要一个非连续时间模型——计算机的数字模型。本文的主要目的是帮助大家了解如何实现数字信号处理。我们将会比较自己录制的声音和一个失真信号，从中寻找2个语音信号之间的相似点和不同点。

对于这个项目，有一点比较重要：我们应该在应用不同的参数时，着重了解波形模式以及它们如何随时间变化。在本文（第1部分）中，我们将探讨语音信号的一些特性以及如何使用MATLAB处理这种信号；然后，我们使用Arduino对录制的语音信号进行详细分析。

• Audacity

• Matlab

• Arduino IDE

处理语音信号时，我们要了解“信号”的含义，这一点很重要。那信号是什么？

通信信号处理 ，作者Paolo Prandoni与Martin Vetterli：

“信号”是对随时间或空间演变的现象的一种形式描述；通过信号处理，我们可以描述任何手动或“机械”操作，从而修改、分析或操控一个信号中包含的信息。我们举个环境温度的简单例子：我们就这个物理变量的正式模型达成一致——比如摄氏度——之后，我们可以用各种方式记录温度随时间的变化，而结果数据集就代表一个温度“信号”。

第一步，我们将了解语音信号的属性。录制自己的声音之前，让我们首先在Audacity中了解一些不同的参数。

声道数量：

• 单声道：您使用一个声道进行录音，这意味着只有一个音频信号——录音分布在同一音量级别。因此如果您有两个或更多扬声器，您听不出差异。这是最常用的方法，因为声音是用一个麦克风录制的，这意味着单声道占用的带宽较少，因此对许多应用（比如电话和无线电）来说非常有用。对于不太熟悉音频设备放置技术细节的用户来说，单声道是正确的选择。

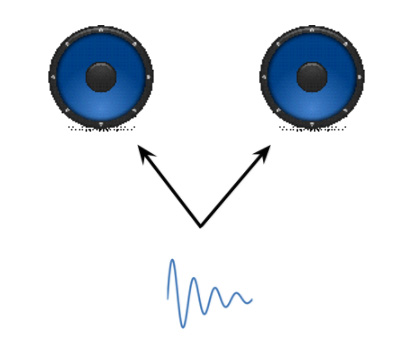
图1：单个音频信号在同一音量级别上分配给多个扬声器（单声道）

• 立体声：您用两个或更多声道录音。由于信号来自多个信号源，因此能够描述声音的方向和位置。使用立体声设置意味着您需要将至少2个麦克风放置在适当的位置。通过这种方式，您可以确定多个声源的不同位置。这种录制通常用于电影和音乐，以获得更广泛的声场解析。

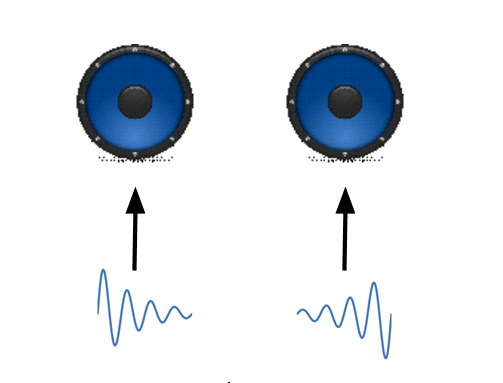
图2：两个或多个信号通道分配到扬声器（立体声）

项目速率（采样率）：在一秒内对连续时间信号的采样次数，然后将其转换为离散时间信号（数值）。采样的度量单位是S/s（即每秒采样数）。

由于音频信号是模拟信号，我们需要将其转换为数字信号，以便由计算机进行处理。我们可以使用下面的采样定理完成此操作。

我们假设有一个模拟信号，如下图所示。想象一下，您需要向您的朋友描述这个信号。这项任务并不是最简单的任务。在这种情况下，将信号描述为数字序列将更加简单。

图3：模拟信号示例

每个样本都以其自身的幅度进行描述。用户可以根据自己的喜好选择采样率。下图显示了如何根据采样定理将模拟信号转换为数字信号。

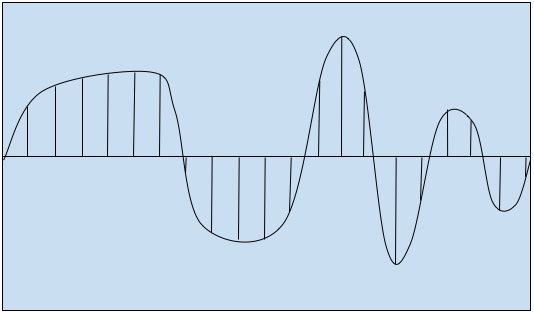
图4：模拟信号转换为数字信号

采样率必须根据人类听觉范围——20Hz至20000Hz——进行选择。为了能够获得特定信号（即准确声音）的所有必要信息，我们的采样率必须满足以下奈奎斯特-香农定理才能将其转换为离散时间信号：

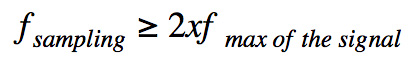
采样率必须大于信号频谱中最高（最大）频率的两倍。在我们的例子中，最大频率为20000Hz。

本项目我们选择48000Hz——这是处理音频信号时的一个标准值。在这种情况下，信号处理时连续时间信号中的所有信息都没有丢失。

说到采样率，一般有2种情况：

• 过采样 – 维基百科

采样频率显著高于奈奎斯特速率。从理论上讲，如果以奈奎斯特速率或高于奈奎斯特速率进行采样，就可以完美重建有限带宽的信号。奈奎斯特速率的定义为信号中最高频率分量的两倍。

• 欠采样 （或走样） – 维基百科

这种技术以低于其奈奎斯特速率（高截止频率的两倍）的采样率采样带通滤波信号，但是仍然能够重建信号。如果以欠采样方式采样一个带通信号时，采样点与高频信号的低频分量采样点无法区分（即信号变得难以区分）。

接下来，我们通过正弦波进行演示。

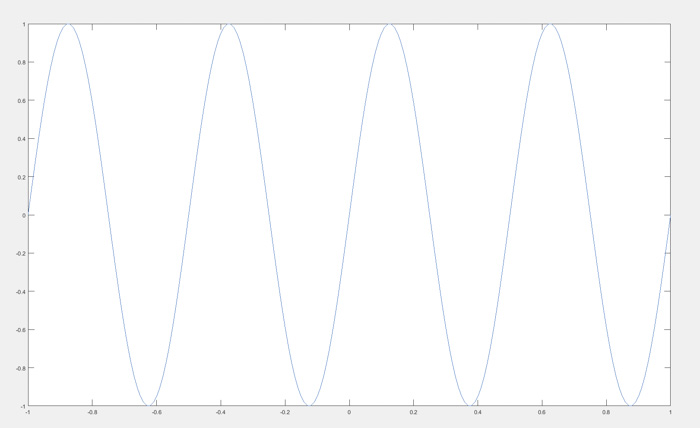
图5：一个正弦波（在MATLAB中绘制）

这是一个频率为2Hz、时域为[-1,1]的正弦波。该波形包含4个周期，这意味着每0.5秒（1/2 Hz）发生一个周期。我们会对这个信号实施多种采样案例，以了解采样的工作原理。

采样点数表示在一个周期内添加了多少个点，并这些点会用插值算法连接起来。一个周期的最小点数应为20，否则线性插值信号看起来就会失真。这尤其适用于平滑的模拟信号，采样后会丢失圆边图案。点的数量越多，采样信号越准确。

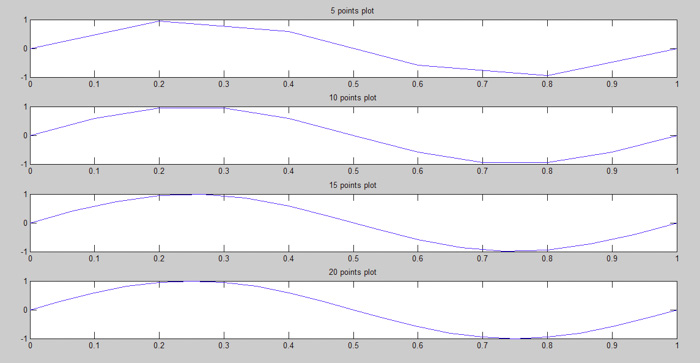
图6：正弦波的必要点数（在MATLAB中绘制）

在本教程中，我们会在MATLAB中绘制一些正弦波，并观察采样频率不同时这些正弦波的行为。在语音信号系列的第二部分中，我们将使用MATLAB进行傅立叶分析。使用Arduino时，MATLAB也是一个非常有用的工具，因为它可以利用串行接口很好地进行通信。我们将在本系列的第三部分中详细介绍如何用Arduino录制语音信号并在MATLAB中进行处理。

对于那些不完全熟悉MATLAB的人，绘制函数的一般步骤如下所示：

要创建脚本或函数，请转到 [HOME] → [New] ，然后选择“Script”（脚本）或“Function”（函数）。

要绘制图7中所示的正弦波，我们需要创建一个Script。复制并粘贴以下代码：

f = 1 points = 5; t = 0:1/points:1; wave = sin(2*pi*f*t); subplot(4,1,1) plot(t,wave) title('5 points plot') points1 = 10; t = 0:1/points1:1; wave1 = sin(2*pi*f*t); subplot(4,1,2) plot(t,wave1) title('10 points plot') points2 = 15; t = 0:1/points2:1; wave2 = sin(2*pi*f*t); subplot(4,1,3) plot(t,wave2) title('15 points plot') points3 = 20; t = 0:1/points3:1; wave3 = sin(2*pi*f*t); subplot(4,1,4) plot(t,wave3) title('20 points plot')

要查看结果，您只需按 Run 按钮即可。

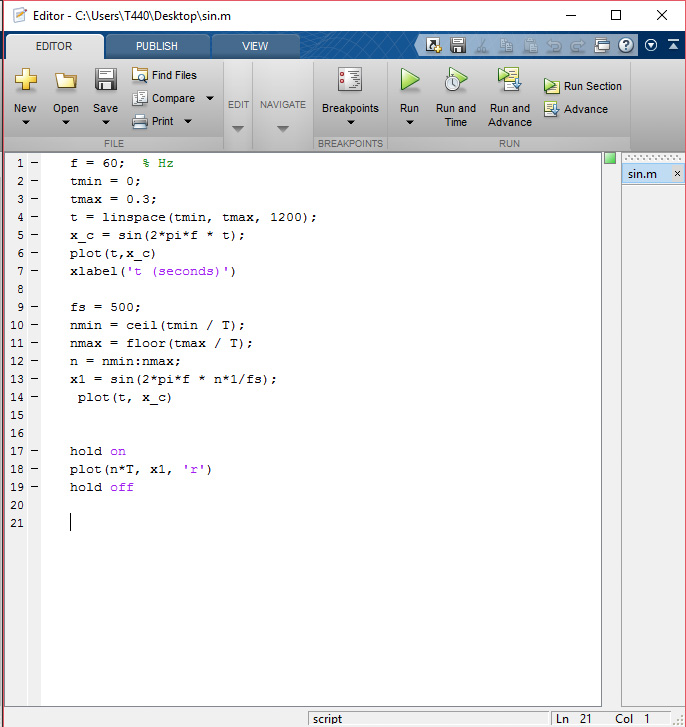
我们还需要创建另一个图——就在刚刚创建的图上绘制，以查看我们对信号进行采样时信号的形式如何变化。信号长度我们选取0.5秒，但是频率增加为60。我们处理的点数也修改为频率数的20倍。假设在这个区间内我们以50Hz的频率进行采样；这意味着每个点都位于T=1/50（其中T是采样周期）处。图7中的小红点就是信号上的采样点。

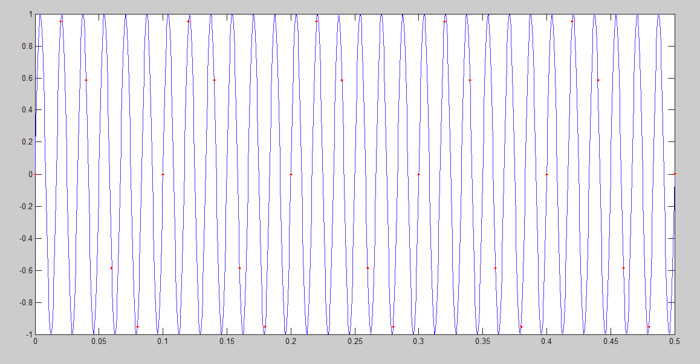
图7：欠采样正弦波

在图7中，由于缺少采样点，我们无法掌握原始信号的形状。连接采样点后，由于信号的点不足，红色信号的形状异常（图8）。这些点无法以正弦形式插值，红色信号不能重建蓝色信号。

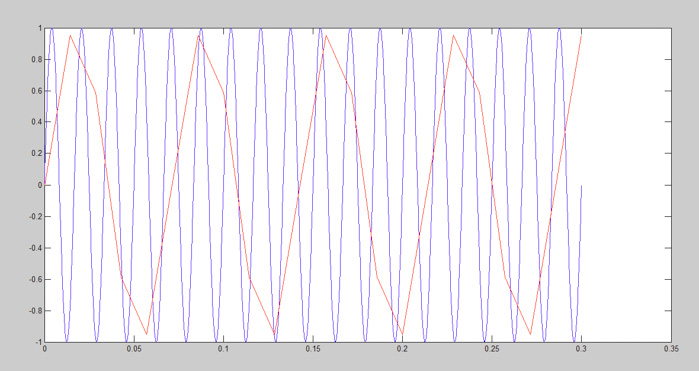
图8：正弦波，fs = 50 Hz

图9：正弦波，fs = 240 Hz

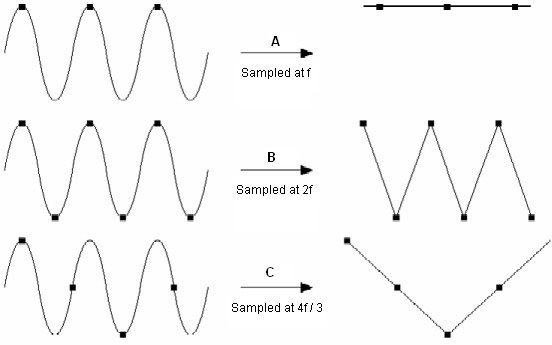
图10： 采样频率示例

如图9和图10所示，当我们以2倍频率进行采样时，图中的唯一采样点就是顶部和底部的最大值。根据采样定理，这两个点足以重建信号。

上文介绍了信号及其属性。现在我们需要用一个实际例子进行测试。Audacity的录音属性如下：

• 采样率： 48000 Hz

• 位数： 16

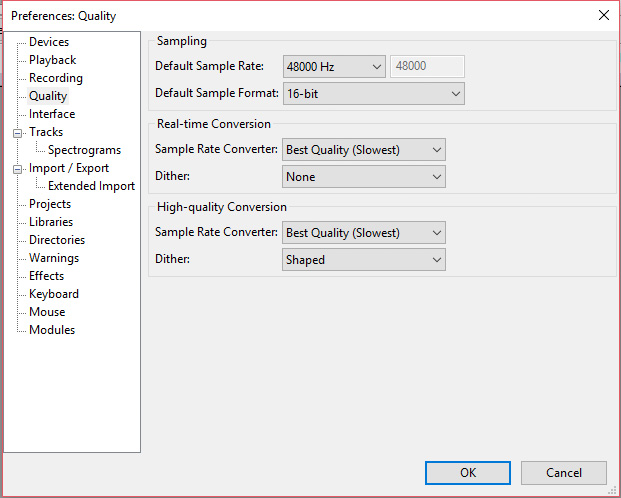
图11：Audacity录制所需的设置

信号长度应至少为10秒左右（项目会进行许多处理，因此不建议超过20秒）。

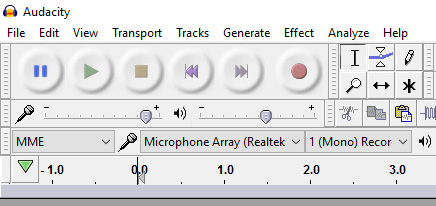
图12：Audacity

与其他录制平台相比，Audacity非常直观。在下图中，您可以看到一个中间有圆圈的红色按钮（record 图标） – 这就是开始录音的按钮。要停止录制，只需按下黄色方块按钮（stop 按钮）即可。程序会记录录音的声波，并将其绘制处理，如下图所示。

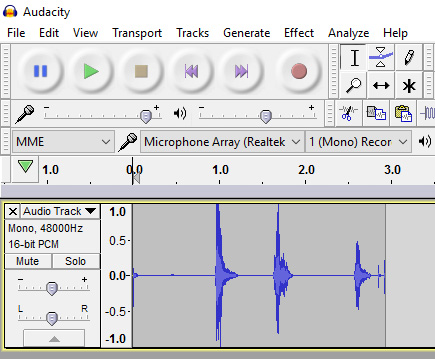
图13：录制的音频信号

第1部分简要介绍了数字信号处理理论。我们使用MATLAB探索了不同的信号波形，并用Audacity录制了自己的声音。在下一个教程中，我们将深入探讨“处理”的更多细节。我们将涉及各种算法和时频域。我们会继续利用MATLAB作为函数编写的主要工具，以处理我们录制的语音并获得分析结果。