第四讲 逻辑函数的公式化简法
2 . 4 . 1 化简的意义与标准
一、化简逻辑函数的意义
二、逻辑函数式的几种常见形式和变换
三、逻辑函数的最简与-或式
2 . 4 . 2 逻辑函数的代数化简法
一、并项法
二、吸收法
三、消去法
四、配项法
2 . 4 . 3 代数化简法举例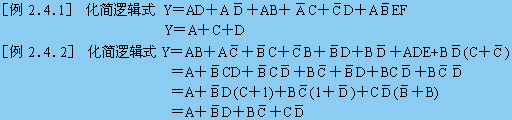
作业:P35 2.1
2.4 逻辑涵数的公式化简法
2 . 4 . 1 化简的意义与标准
一、化简逻辑函数的意义
根据逻辑问题归纳出来的逻辑函数式往往不是最简逻辑函数式,对逻辑函数进行化简和变换,可以得到最简的逻辑函数式和所需要的形式,设计出最简洁的逻辑电路。这对于节省元器件,优化生产工艺,降低成本和提高系统的可靠性,提高产品在市场的竞争力是非常重要的。
二、逻辑函数式的几种常见形式和变换
常见的逻辑式主要有5种形式,如逻辑式![]() 可表示为
可表示为

三、逻辑函数的最简与-或式
对与或式而言:
最简:
2 . 4 . 2 逻辑函数的代数化简法
一、并项法![]()


2 . 4 . 3 代数化简法举例
在实际化简逻辑函数时,需要灵活运用上述几种方法,才能得到最简与-或式.
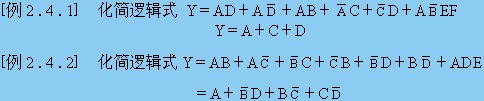

 我要赚赏金
我要赚赏金

