卡诺图
卡诺图是逻辑函数的图形表示。利用卡诺图可以简化逻辑函数。
卡诺图的构成
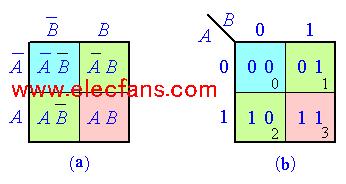
卡诺图是最小项按一定规律排列的方格图,每一个最小项占有一个小方格。因为最小项的数目与变量数有关,设变量数为n,则最小项的数目为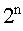 。二个变量的卡诺图见下图所示。图中第一行表示
。二个变量的卡诺图见下图所示。图中第一行表示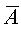 ,第二行表示A;第一列表示
,第二行表示A;第一列表示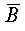 ,第二列表示B。这样四个小方格就由四个最小项分别对号占有,行和列的符号相交就以最小项的与逻辑形式记入该方格中。
,第二列表示B。这样四个小方格就由四个最小项分别对号占有,行和列的符号相交就以最小项的与逻辑形式记入该方格中。
三变量卡诺图
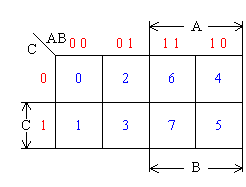
三变量卡诺图由8个最小项m0—m7组成,每个最小项占一个方格;
AB组合中左数位代表A变量,右数位代表B变量。沿横向从一个方格进行到下一个方格时,两个数位只变化一个; 原变量与非变量各占4格。
四变量卡诺图
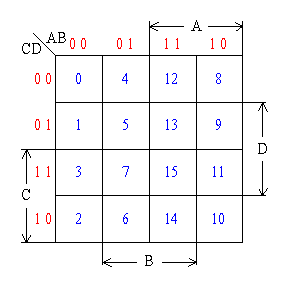
卡诺图的有用组合
卡诺图二方格相邻组合
几何相邻的两个最小项是逻辑相邻的(两个最小项中只有一个变量不同);
有些方格几何上不相邻,但逻辑上却是相邻的;
任何两个最小项可以合并成最小项,且可减少一个变量。
【例3】四方格卡诺图中,有F(A,B,C,D)=∑m(2,3,8,10,12)
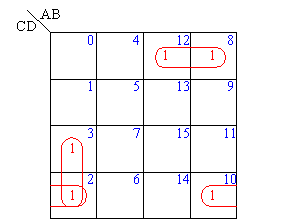
第一种组合方式:
| _ _ | ||
| m8+m12= | A C D | (几何相邻) |
| _ _ | ||
| m2+m3= | A B C | (几何相邻) |
| _ _ | ||
| m2+m10= | B C D | (几何不相邻,逻辑相邻) |
第二种组合方式:
| _ _ | ||
| m8+m12= | A C D | |
| _ _ | ||
| m2+m3= | A B C | |
| _ _ | ||
| m8+m10= | A B D | (几何不相邻,逻辑相邻) |
| F(A,B,C,D) | =∑m(2,3,8,10,12) |
| _ _ _ _ _ _ | |
| =A C D + A B C + B C D | |
| _ _ _ _ _ _ | |
| =A C D + A B C + A B D |
两种表达式虽然形式不同,但逻辑上是等价的。另外,m2、m8重复使用是允许的。
卡诺图四方格相邻组合
四方格相邻时,4个最小项可合并成1项,且可消去两个变量。
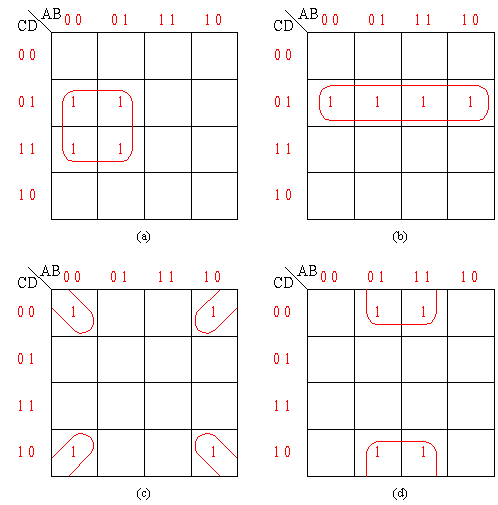
图(a)中,
| _ | |
| F(A,B,C,D)=∑m(1,3,5,7)= | AD |
图(b)中,
| _ | |
| F(A,B,C,D)=∑m(1,5,9,13)= | CD |
图(c)中,
| F(A,B,C,D)=∑m(0,2,8,10)= | ? |
图(d)中,
| F(A,B,C,D)=∑m(4,6,12,14)= | ? |
卡诺图八方格相邻组合
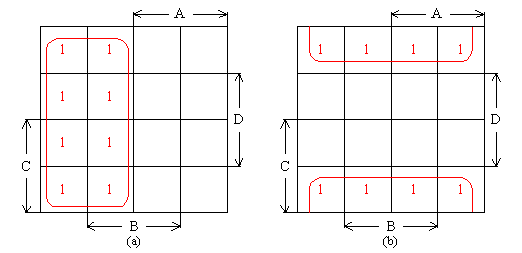
图(a)中,F(A,B,C,D)=∑m(0,1,2,3,4,5,6,7)=Ã
图(b)中,F(A,B,C,D)=∑m(0,4,12,8,2,6,14,10)=?
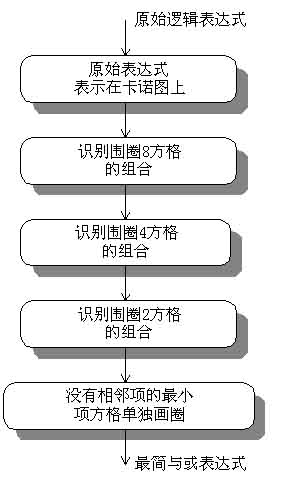
用卡诺图简化逻辑函数
简化规则
必须使每个方格(最小项)至少被包含一次;
使每个组合包含尽可能多的方格;
所有的方格包含在尽可能少的不同组合中。
简化步骤
 逻辑函数未用最小项表示的简化逻辑函数未用最小项表示照样可以化简。如果F采用与—或表达式,在填入卡诺图过程中就能把函数展开成最小项。 具有无关项的化简
逻辑函数未用最小项表示的简化逻辑函数未用最小项表示照样可以化简。如果F采用与—或表达式,在填入卡诺图过程中就能把函数展开成最小项。 具有无关项的化简无关项又叫任意项,是一种最小项,其值可以取0或1。利用无关项这一特点,可以使函数简化。
用卡诺图化简逻辑函数的步骤
如果表达式为最小项表达式,则可直接填入卡诺图
如表达式不是最小项表达式,但是“与—或表达式”,可将其先化成最小项表达式,再填入卡诺图。也可直接填入。
合并相邻的最小项,即根据下述原则画圈
尽量画大圈,但每个圈内只能含有2n(n=0,1,2,3……)个相邻项。要特别注意对边相邻性和四角相邻性。
圈的个数尽量少。
卡诺图中所有取值为1的方格均要被圈过,即不能漏下取值为1的最小项。
在新画的包围圈中至少要含有1个末被圈过的1方格,否则该包围圈是多余的。
写出化简后的表达式。每一个圈写一个最简与项,规则是,取值为l的变量用原变量表示,取值为0的变量用反变量表示,将这些变量相与。然后将所有与项进行逻辑加,即得最简与—或表达式。
在进行化简时,如果用图中真值为0的项更方便,可以用他们来处理,方法和真值取1时一样,只是结果要再做一次求反。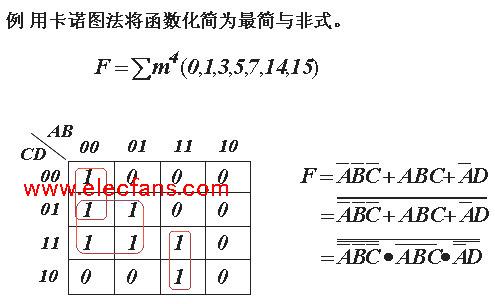

 我要赚赏金
我要赚赏金

