1261年,中国宋朝的杨辉著《详解九章算法》
| |
杨辉最重要的著作是《详解九章算法》.为了使《九章算术》便于自学,杨辉对该书的246个问题中较难的80题作了详解,并增添了“图解、乘除算法和纂类”三卷.“详解”包括三个方面:一是“解题”,即解释题意、名词术语,校勘文字,并对题目作出评注;二是“细草”,即详细的解题过程及必要的图示;三是“比类”,即增选与原题算法相同或类似的例题进行对照分析.“纂类”是把《九章算术》中的全部问题按解题方法由浅入深的顺序重新整理分类.
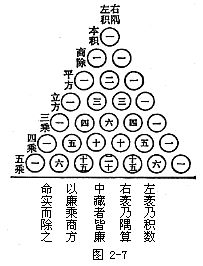
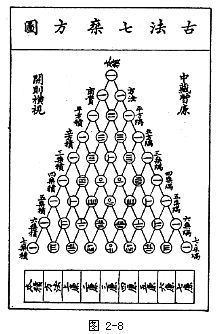
在《详解九章算法》中载有一张珍贵的图形——“开方作法本源”图(图2-7).根据杨辉自注,此图“出《释锁算书》,贾宪用此术”.就是说,这张图是贾宪(11世纪)创造的,原载于《释锁算书》(已失传)中,这张图实际上是一个二项式展开式的系数表,它包括了0次到6次二项式的全部系数.这些展开式用现代数学符号表示就是: (a+b)0=1 (a+b)1=a+b (a+b)2=a2+2ab+b2 (a+b)3=a3+3a2b+3ab2+b3 (a+b)4=a4+4a3b+6a2b2+4ab3+b4 (a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 (a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6 表中的系数具有一定规律,每一行比上一行多一个数,每行除左右两个“一”外,每个数都是其“肩”上两个数之和. 因此这个表可以这样继续往下造.后来,元朝的朱世杰把它扩展为“古法七乘方图”(图2-8),载于《四元玉鉴》一书中. 贾宪制作这张表进行开方运算,因其形似三角形,因此我们称之为“贾宪三角形”.欧洲人一般称它为“帕斯卡三角形”,认为是法国科学家帕斯卡(B.Pascal,1623~1662)首创的.近年来,国外也逐渐承认这项成果属于中国,有些数学史书上开始称它为“中国三角形”(Chinese triangle)了. 杨辉在数学教育方面也有重要贡献.他特别重视数学的普及教育,亲手编写了多种教材并制定出详细的教学计划.在教学安排上,他强调由浅入深,循序渐进.在《乘除通变本末》一书中,他为初学者制订了“习算纲目”,列出了学习内容,先后顺序及进度安排等,这是中国数学教育史上的一个重要文献.
杨辉很注意数学在实际中的应用.他在《日用算法》中提出:“以乘除加减为法,称斗尺田为问;用法必载源流,命题须责实有”.要求数学教学的内容必须联系实际,应以社会实践中提出的计算问题为主.这正是中国古代数学的优良传统之一. 在教学方法方面,杨辉注意深入浅出,直观形象,他很注意讲清题意,在《详解九章算法》中加了“解题”一项,要学习者“全要认题之主意”,避免误解题意而出错.在该书中还特意增加了一卷图形,有些题目既有“题图”,又有“法图”,直观形象,让人一目了然.另一方面,他又注重引导与启发,他说:“好学君子自动触类而考,何必尽传”. 在学习方法上,他提倡熟读精思,融会贯通.他主张学习要在广博的基础上深入,对各种算法应分门别类地仔细钻研,消化理解并广泛熟悉它们的各种应用,反对死记硬背. 对于培养计算能力,杨辉很强调要“多练”.每个学习单元他都规定要完成一定数量的练习,认为这样可以“庶久而无失念”.他对做练习与学习数学基础知识的关系有独到的见解:“夫学算者题从法取,法将题验,凡欲明一法,必设一题”.他还要求习题应具典型性,起到“举一(例)而三隅反”的作用. 杨辉治学严谨,在教学上一丝不苟.他对学习中的细小环节也不放过,特别是容易忽视或出错之处,他在书中都反复强调,并列为学习的重点. 作为我国古代卓越的数学教育家,杨辉提出的这些教育原则和主张至今仍有积极意义. |
共1条
1/1 1 跳转至页
详解九章算法 作者:杨辉
关键词: 算
共1条
1/1 1 跳转至页
回复
| 有奖活动 | |
|---|---|
| 这个春节你犒赏自己什么了?分享你的故事,有奖征集 | |
| 2026年“我要开发板活动”第三季,开始了! | |
| 硬核工程师专属补给计划——填盲盒 | |
| “我踩过的那些坑”主题活动——第002期 | |
| 【EEPW电子工程师创研计划】技术变现通道已开启~ | |
| 发原创文章 【每月瓜分千元赏金 凭实力攒钱买好礼~】 | |
| 【EEPW在线】E起听工程师的声音! | |
| 高校联络员开始招募啦!有惊喜!! | |
 我要赚赏金打赏帖 我要赚赏金打赏帖 |
|
|---|---|
| Gravity:中英文语音合成模块V2.0及其串口控制被打赏¥24元 | |
| 全彩色度变化图的绘制被打赏¥27元 | |
| 【FreeRtos】FreeRtos任务栈的生长方向管理方式被打赏¥20元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】LVGL添加输入设备:EC11旋转编码器被打赏¥39元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】RA8D1部署FreeRTOS+LVGL被打赏¥33元 | |
| 空气质量检测器设计与实现被打赏¥24元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】LWIP进行UDP、TCP、HTTP、MQTT功能联合测试被打赏¥41元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】RA8D1部署FreeRTOS+LWIP被打赏¥36元 | |
| RTOS怎么选?让我来给你答案!被打赏¥15元 | |
| 【S32K3XX】Flash驱动使用被打赏¥26元 | |