EEPW论坛

1. 雷诺数的发现

1883年英国人雷诺(O.Reynolds)观察了流体在圆管内的流动，首先指出，流体的流动形态除了与流速(ω)有关外，还与管径(d)、流体的粘度(μ)、流体的密度(ρ)这3个因素有关。

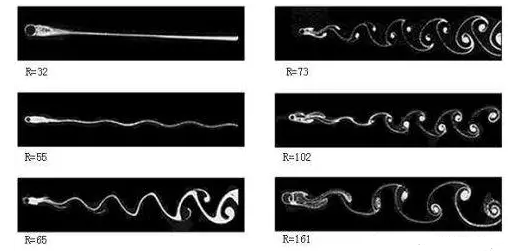
2. 雷诺数的定义

雷诺数是流体力学中表征粘性影响的相似准则数。为纪念O.雷诺而命名，记作Re。

雷诺数，又称雷诺准数，是用以判别粘性流体流动状态的一个无因次数群。

Re=ρvL/μ

上面是雷诺数的数学公式，ρ、μ为流体密度和动力粘性系数，v、L为流场的特征速度和特征长度。

对外流问题，v、L一般取远前方来流速度和物体主要尺寸(如机翼弦长或圆球直径)；内流问题则取通道内平均流速和通道直径。两个几何相似流场的雷诺数相等，则对应微团的惯性力与粘性力之比相等。

3.雷诺数的物理意义

雷诺数物理上表示惯性力和粘性力量级的比。

雷诺数较小时，粘滞力对流场的影响大于惯性，流场中流速的扰动会因粘滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性对流场的影响大于粘滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的紊流流场。关于湍流，可以阅读在下的这篇文章《CFD工程仿真中基本用到湍流模型，你真的深入了解过湍流吗》，《Fluent提供了9个湍流模型，教你如何选择》。

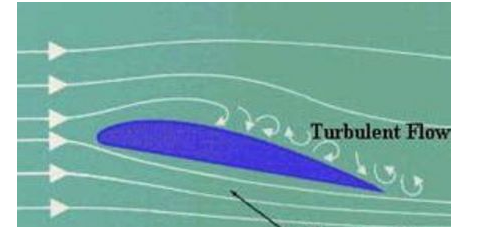
4. 雷诺数的由来

雷诺数可以从无量纲化的非可压N-S方程推导出来： 

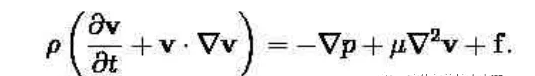
上式中每一项的单位都是加速度乘以密度，无量纲化上式，需要把方程变成一个独立于物理单位的方程。把上式乘以系数： 

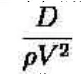
无量纲的N-S方程可以写为：

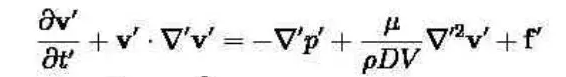
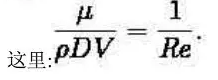
为了阅读方便将撇去掉： 

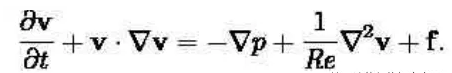
这就是为什么在数学上所有的具有相同雷诺数的流场是相似的。

5. 临界雷诺数

临界雷诺数（critical Reynold’s number），当流体在管道中、板面上或具有一定形状的物体表面上流过时，流体的一部或全部会随条件的变化而由层流转变为湍流，此时，摩擦系数、阻力系数等会发生显著的变化。转变点处的雷诺数即为临界雷诺数。

通过雷诺实验人们认识到，流动存在以下三种不同的状态。第一种，流体的质点之间互不掺混、质点的运动轨迹为有条不紊的层状流动，称为层流；第二种，流体的质点之间相互掺混、质点的运动轨迹为杂乱无章的流动，称为紊流；第三种，表现为层流到紊流或紊流到层流的过渡，称为过渡状态。随流速的变化而呈现不同的流动状态，是自然界中一切流体运动普遍存在的物理现象。

对于任何管径和任何牛顿流体（切应力与速度梯度符合牛顿内摩擦定律的流体）Re在2000～4000正好是流体由层流向紊流转变的过渡区，工程上为了简便起见，便把Re=2000作为流态是层流还是紊流的判别条件。

6.雷诺相似准则

两个流动的惯性力和粘滞力成比例，则它们的雷诺数相等，这就是雷诺准则，或称为粘滞力相似准则。

7. 雷诺数效应

雷诺数效应是指随着雷诺数变化，静力三分力系数、表面压力系数及其分布、Strouhal数等参数也是变化的。

雷诺数效应有两层意思：其一，某些参数是雷诺数的函数，雷诺数是这些参数变化的内因；其二，与模型试验有关，当模型的缩尺很小时，模型与原型的雷诺数相差很大，试验数据向原型复原时，无法得到参数的实际变化规律，这是因为试验设计时没有满足雷诺数相似准则而产生的。

8. 典型雷诺数

普通航空飞机：5 000 000

小型无人机：400 000

海鸥：100 000

滑翔蝴蝶：7000

圆形光滑管道：2500

橡胶管道：1600~2100

精子：0.0001

大脑中的血液流 ：100

主动脉中的血流 1000

转帖自网络