在上一篇文章《你好,我叫采样,来认识一下呗!》中,我们介绍了奈奎斯特-香农定理。我们看到,当波形采样频率不能提供每个周期至少2个样本时,正弦波的频率特性就会彻底丢失。换句话说,如果我们以低于奈奎斯特速率的频率进行采样,那么将无法完美地重构正弦信号。
然而,大多数信号都不是单频正弦信号。例如,受调制的射频信号具有与载波和基带波形相关的频率,并且表示人类语音的音频信号将覆盖一定范围的频率。
我们使用傅立叶变换对信号频率进行可视化处理。在单频信号的情况下,时域图是一种表达“采样率不足的影响”的好方法,但对于其他类型的信号,我宁愿使用频域。
采样的频域效应
假设我们要对一个音频信号进行数字化处理,这个音频信号包含了一定范围内的多种不同频率的混合信号。该范围的高端被定义为fMAX,我们假设范围延伸到了DC,即使我们听不到那么低的频率。这样一个信号的傅立叶变换,可能看起来是这样的:
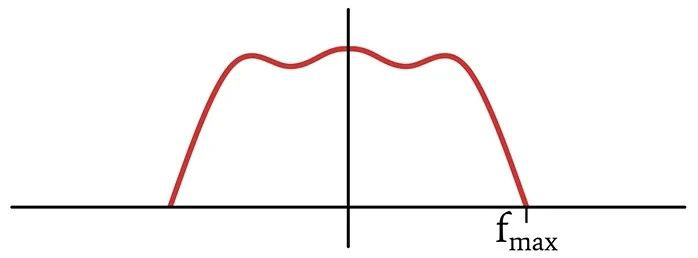
时域的数学采样
在数学领域,理想的采样相当于原始时域波形乘以一系列增量函数,这些函数之间的间隔等于1/f样本,我们称之为T样本。(在本文的其余部分,我们将使用fS表示f样本、使用TS表示T样本。)这种乘法使得采样信号在增量函数之间为零,并在与增量函数重合的每个时间点上保留原始信号的值。
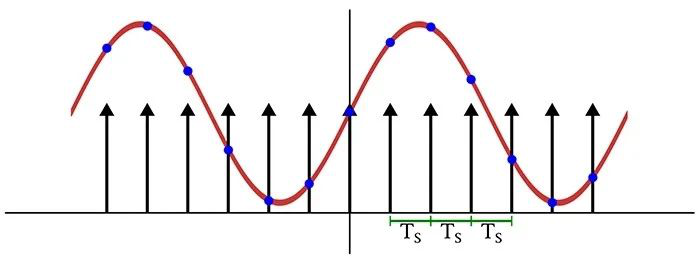
(数学上实现的时域采样:我们将模拟信号乘以一系列在采样频率处出现的增量函数)
频域的数学采样
这种时域采样过程是如何影响信号频域表示的?下面,让我们一起来看看。
首先要记住的是,时域信号相乘相当于频域卷积。因此,我们可以通过将原始信号的傅立叶变换与增量函数的傅立叶变换进行卷积,从而得到采样信号的傅立叶变换。
事实证明,增量函数的傅立叶变换是一个增量函数序列。而不同之处则在于,增量函数是被与采样频率相对应的水平距离分隔的,而不是采样周期。
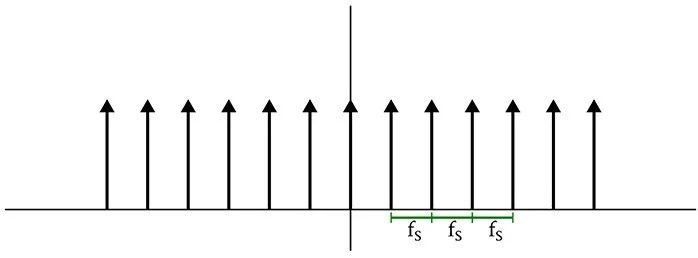
![]() (由采样周期分隔的增量函数序列的频谱,是由采样频率分隔的一系列增量函数)
(由采样周期分隔的增量函数序列的频谱,是由采样频率分隔的一系列增量函数)
当我们将增量函数的频谱与原始信号的频谱进行卷积时,我们就得到了原始频谱的副本,这些副本会按照增量函数的位置进行移位。因此,采样信号的频谱是由多个以±fS、±2fS、±3fS等为中心的相同的“子频谱”组成的。
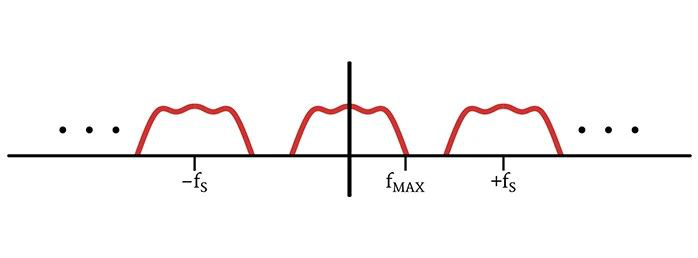
(适当的采样频率会导致子频谱发生移位,以保持完全分离)
现在,我们有了通过频域分析来证明奈奎斯特-香农定理所需的信息了。这个定理,正如我在上一篇文章中所表述的:
如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样,那么原始模拟信号就能从采样产生的离散值中完全恢复。
由于傅立叶变换的负频率部分,原始信号的全部数学带宽为2fMAX。因此,为了确保子频谱不重叠,我们必须将其移位至少2fMAX。换句话说,采样频率必须比信号的最大频率高出至少两倍。
如果满足这个条件,那么原始信号就能实现完美重构。但你知道这是为什么吗?因为原始频谱没有改变,所以我们可以通过低通滤波来消除其他子频谱。(下一篇文章将会详细地探讨这个话题。)如果不满足这个条件,那么子频谱就会重叠,原始频谱就会改变,即使再强的低通滤波也不能恢复原始信号。
混 叠
子频谱重叠是当我们使用低于奈奎斯特速率的采样频率时,信息被破坏而造成的。子频谱的重叠部分通过加法合并起来;如果我们试图使用低通滤波器分离出原始频谱,那么重叠波段的频率含量就会不同,因此相应的时域信号也会不同。
这种现象就称之为混叠。
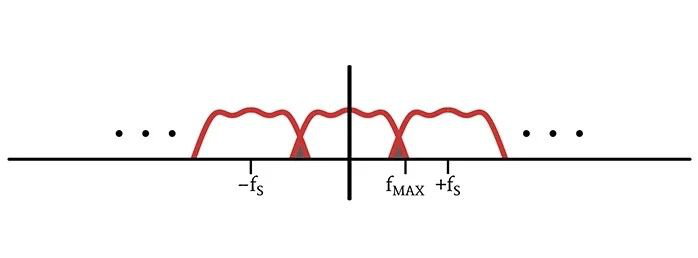
(三角形棕色阴影部分表示引起频谱变化的混叠)
名词“别名”的释义之一是“虚假或者假定的身份”,我们之所以使用“混叠”一词,是因为这种采样现象会导致一个频率分量移到频谱中的一个新位置,从而将自己“伪装”成一个不同的频率。
我们在上一篇文章中看到了这一点,1.1f信号下采样所产生的离散时间波形,其频率似乎远低于原始模拟波形的频率。

 我要赚赏金
我要赚赏金

