EEPW论坛

  如何使用降阶隆伯格观测器（ROLO）估算永磁同步电机（PMSM）的转子磁链位置。首先介绍特征值与稳定性的关系；在此基础上，引入状态反馈控制的理念；接着介绍如何使用该理念来设计隆伯格观测器；然后，以PMSM为例，推导ROLO的设计过程，给出设计结果；最后，介绍Microchip的相关电机控制方案（评估套件、例程和文档等）。

一、概述

永磁同步电机（PMSM）的磁场定向控制（FOC）在近十几年成为了主流的电机控制方法。其中，无位置传感器FOC由于其低成本和高可靠性，获得了越来越多的应用和关注。由于没有位置传感器，所以必须估算转子磁链位置。由于在旋转过程中，转子磁链生成反电动势（BEMF），并且BEMF超前转子磁链π2弧度，所以可以利用对BEMF进行观测，进而估算转子磁链。降阶隆伯格观测器（ROLO）是一种常用的BEMF观测手段。

一方面，工程师可能不具备设计观测器所需的背景知识；另一方面，产品开发项目必须尽快且高质量地完成。尽管可以找到背景知识的相关教材，但由于其缺少针对性，所以工程师不得不花费大量时间进行学习。该矛盾经常成为制约产品开发进度和质量的瓶颈。针对此困境，ROLO由于其原理简单，成为了能短时间掌握的优选方案。

本文针对PMSM控制所需，筛选出最少量的必需知识，按照逻辑顺序阐述利用ROLO观测BEMF的原理。此外，还介绍了Microchip的相关电机控制方案。读者可以借此快速掌握原理，并且上手实践和熟悉。

二、特征值与稳定性

常微分方程（ODE）是时间确定性系统的一种抽象模型。PMSM可以看作是一个线性时间确定性系统，因此可以用线性常微分方程来建模。

考虑以下的一般线性ODE：

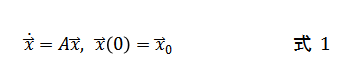
三、状态反馈控制

四、隆伯格观测器

考虑以下系统

式13由斯坦福大学的大卫。隆伯格教授提出，因此命名为隆伯格观测器。

五、观测PMSM的BEMF

在静止两相坐标系（α-β坐标系）中，表贴式PMSM的电压方程为：

应当注意到，式17与式9的形式一致。读者能轻易地看出他们之间的对应关系。于是，只要根据式13就可以直接设计出针对e的隆伯格观测器。对此，本文不做展开，并鼓励读者亲自进行推导。需要指出的是，这样的观测器被称为降阶隆伯格观测器。

六、Microchip的ROLO方案

Microchip的基于ROLO的PMSM无传感器控制方案提供例程、评估套件、开发工具和帮助文档。

例程位于MPLAB®Harmony3的motorcontrol模块中，是一个运行在Cortex®-M0+MCU（SAMC21）之上的MPLABX工程：pmsm_foc_rolo_sam_c21。

该演示方案可以运行于MCLV2低压电机控制评估套件或MCHV3高压电机控制评估套件。两款评估套件均可在Microchip官网搜索并订购。

该例程利用图形化配置工具MPLABHarmony配置器（MHC）生成。使用MPLABXIDE打开该工程，并打开MHC，就可以看到CPU和所需片上周边（PWM模块和ADC等）的配置情况，如图1所示。

相应的帮助文档也位于MPLABHarmony3的motorcontrol模块中。其中介绍了如何搭建硬件平台、编译和下载工程、算法原理框图、软件流程图、软件配置方法等，如图2、图3、图4和图5所示。

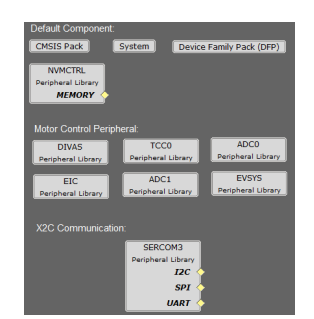
《图1.例程的MHC配置》

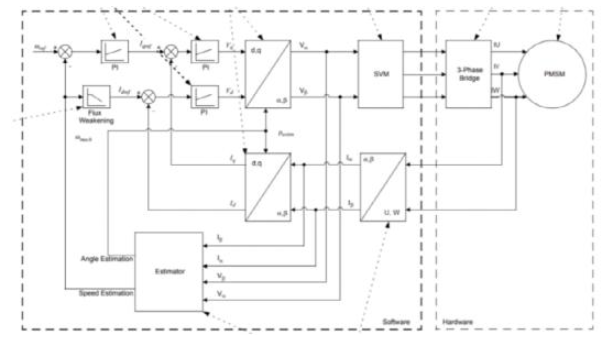
《图2.电机控制算法框图》

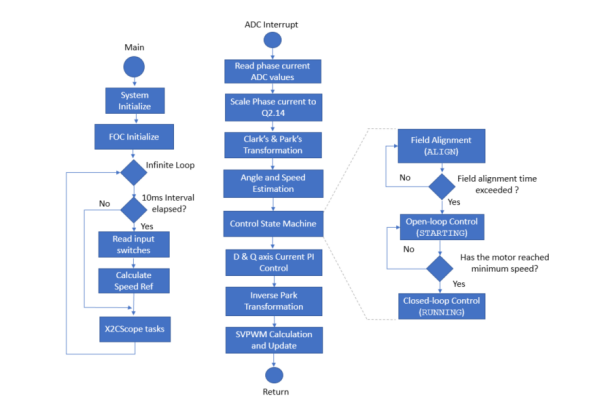
《图3.软件流程图》

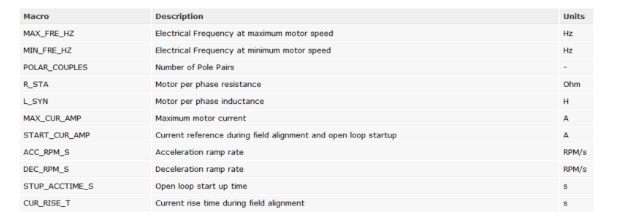
《图4.软件配置方法：电机参数宏定义列表》