EEPW论坛

特勒根定理适用于许多电路网络，只要该网络满足总电流守恒（基尔霍夫电流定律（KCL））且所有闭合回路电压代数和为零（基尔霍夫电压定律（KVL））。特勒根定理在分析电路和与电路相类似的复杂网络（如神经系统、代谢网络、管道网络与化工过程网络）中是一种常用的工具。
应用特勒根定理可方便地证明电路中的互易定理、复功率平衡定理等。
特勒根定理1明确反映了电路实际功率的守恒。但特勒根定理2曾仅仅被认为只有功率守恒的数学形式，却无法与实际电路对应，因此定理2也被称为“拟功率定理” 。定理2后也被证明反映了电路实际功率的守恒 ，并具有共轭性。
现讨论以图G描述的一个有 b 条边和nt个节点的网络。对于一个电路网络，边表示二端元器件，节点处为元件间的电气连接。对图中所有边设其两端电势差为Uk，支路电流为Ik（k=1,2,3...,b）且均取关联参考方向。若所有的回路电压均满足KVL且节点电流都满足KCL，则有：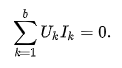

特勒根定理的应用十分广泛，适用于许多电路，无论其是否包含非线性元件、是否是稳恒电路。而且对电流电压做线性变换不影响特勒根定理的成立，因为KCL与KVL不受线性变换影响。例如对电流电压取平均时或拉普拉斯变换下特勒根定理仍然成立。特勒根定理的另一个常用推广是对拓扑结构相同（关联矩阵相同）的两个不同网络的支路电压和电流的积之和仍为零。即：

图所示电路中No为无源电阻网络，已知:当us1= 5V, us2 =0时,i1=IA，i2 =0.5A;当us1=0,us2 = 20V时,i2= -2A。试求us1,和us2 ,共同作用时各电源供出的功率。