EEPW论坛

传递函数的频率特性

这里通过“传递函数的频率特性”来考虑传递函数。和前项的“基尔霍夫定律和阻抗”中的解说有密切的关系所以希望合在一起阅读。

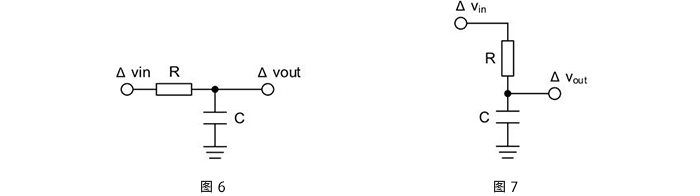
首先，请看图6。电阻和电容器组成简单的闭合电路。首先，尝试计算出本电路的传递函数。

为了让电路图容易形象化，将图6改画成图7。当然，作为电路是相同的。这样一来，能立刻明白ΔVout是ΔVin通过R和C的阻抗分割的。

形成公式ΔVout = ΔVin ×（C/（R+C)），表示阻抗。

正如前项的“基尔霍夫定律和阻抗”说明的那样，虽然R的表示为R，

然后尝试画波特图。波特图是指横轴为频率（⨍），纵轴为增益（Gain）和相位（Phase）的图表，需要计算按增益和相位。首先，从增益开始计算。

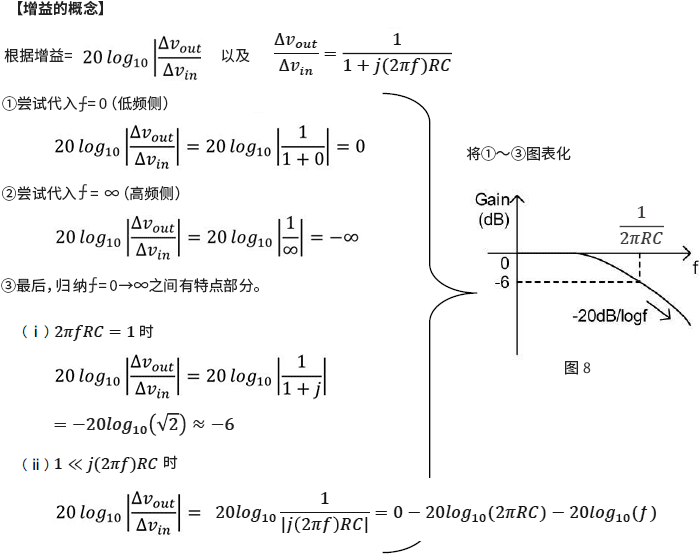
接着，计算相位。

总结上述，如下面的图10所示。至此，可以让增益（Gain）和相位（Phase）的特性形象化。

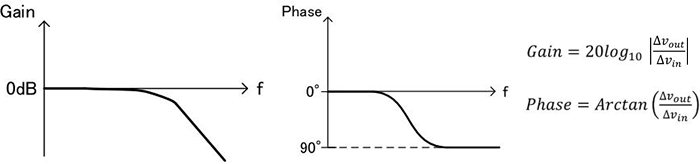
图10

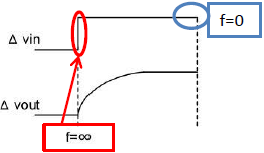
图11

前项“基尔霍夫定律和阻抗”中，讲述了电容器的阻抗表示为“1/jωC”，以达到理解传递函数的目的。请看图11。

图11是指图6的电路的步进响应特性。电容器电源波动的瞬间（与f = ∞等值），电容器的阻抗为0，ΔVout=0。经过一定时间变为（与f=∞等值）ΔVin相等。

接着，图形化如下。这是电容器步进响应针对阻抗“1/jωC”的示意图。

图12

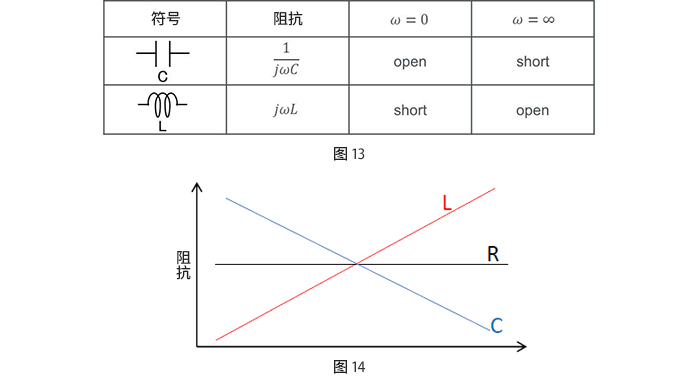
图13中包括线圈的各元件的阻抗记述和ω=0以及ω=∞时的等价处理，而且，图14中表示频率特性。