EEPW论坛

相信很多人都知道Buck电路中输入电容纹波电流有效值，在连续工作模式下可以用以下公式来计算：
然而，相信也有很多人并不一定知道上面的计算公式是如何推导出来的，下文将完成这一过程。

众所周知，在BuckConverter电路中Q1的电流（IQ1）波形基本如图1所示：0～DTs期间为一半梯形，DTs～Ts期间为零。当0～DT期间Iq1 ⊿I足够小时（不考虑输出电流纹波的影响），则Iq1波形为近似为一个高为Io、宽为DTs的矩形，则有：

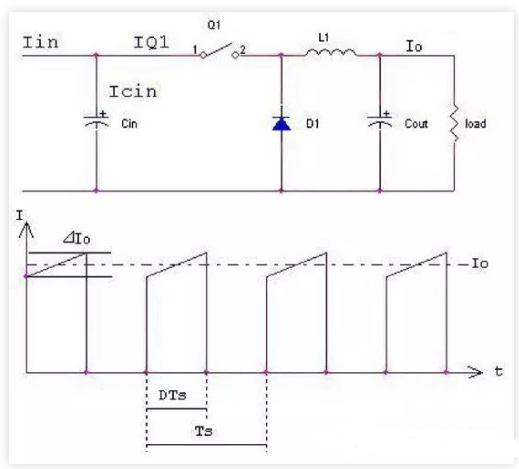图1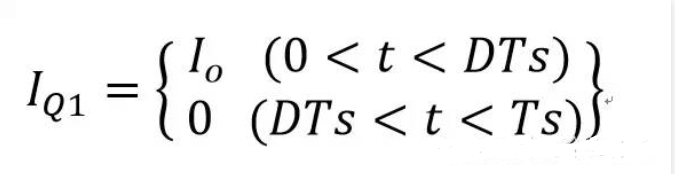
Iin=(Vo/Vin)*Io＝DIo （Iin，只要Cin容量足够大，则在整个周期中是基本恒定的；按照能量守恒定律：Pin≈Pout）Icin＝Iq1-Iin

对Icin 的表达式可以这样理解：在Q1导通期间输入端和输入电容共同向输出端提供电流，因此输入电容电流等于Q1电流减去输入端电流；在Q1关断期间输入端对电容充电，以补充在Q1导通期间所泄掉的电荷，而此时电流方向与所定义的正向是相反的，所以有Icin＝－DIo根据有效值的定义.

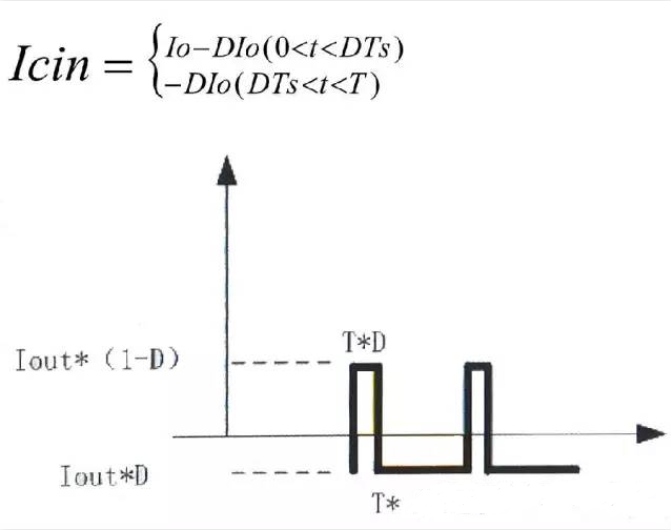
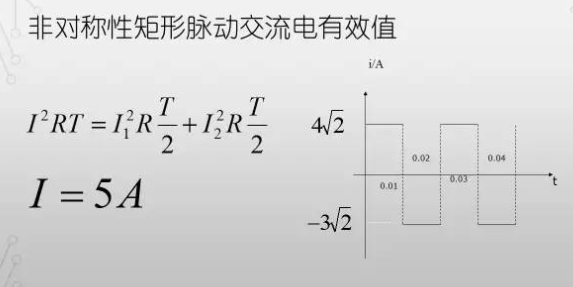
不难得出输入电容的纹波电流有效值Icin.rms的计算公式：

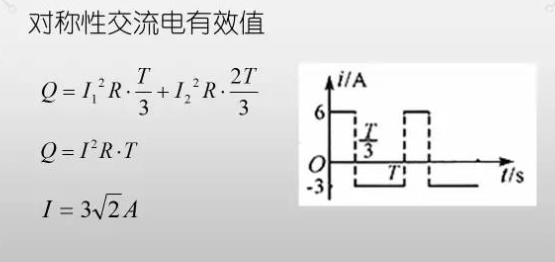
有效值定义：有效值(Effectivevalue)在相同的电阻上分别通以直流电流和交流电流，经过一个交流周期的时间，如果它们在电阻上所消耗的电能相等的话，则把该直流电流（电压）的大小作为交流电流（电压）的有效值，正弦电流（电压）的有效值等于其最大值（幅值）的1/√2，约0.707倍。

在正弦交流电流电中根据热等效原理，定义电流和电压的有效值为其瞬时值在一个周期内的方均根值。

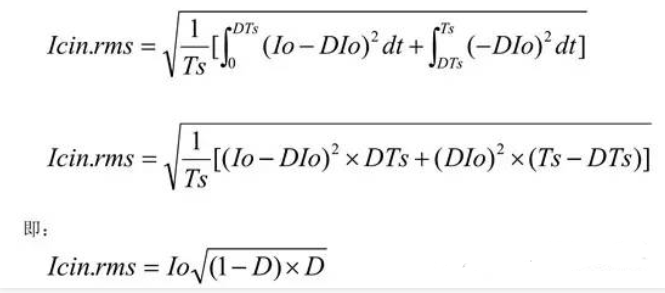
如果考虑输出纹波ΔI，Icin.rms的电流有效值。
在忽略Buck电源的输出电流纹波的前提下，进行的近似计算。那么我们通过精确计算，可以得到一个更准确的数据。
这个推导的过程，利用到积分公式。通过分析和推导，可以对电路的工作原理有比较透彻的理解。
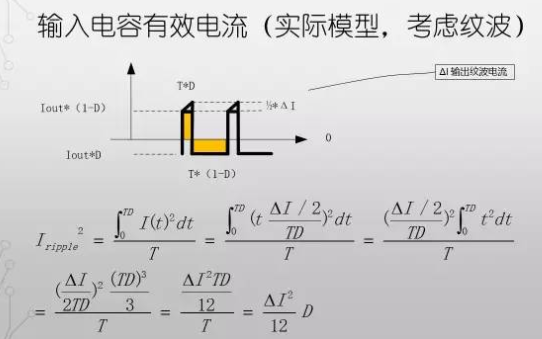
如果考虑输出纹波电流。那么电容上的纹波电流的波形为：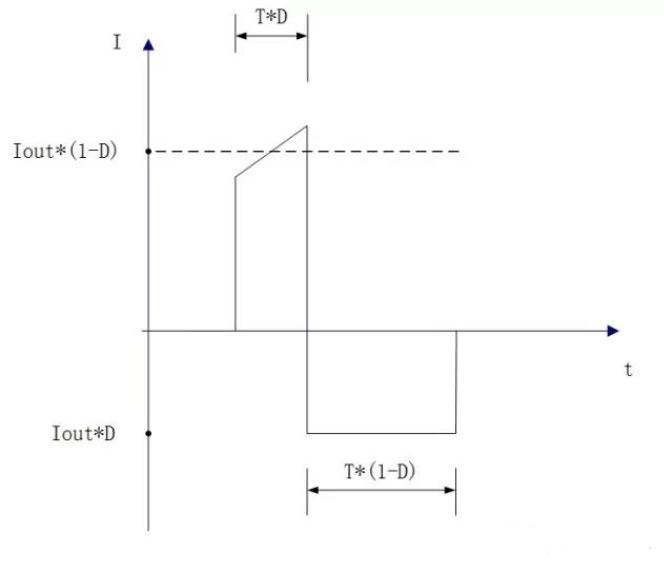

我们了解了脉冲波的有效电流的计算方法之后，我们知道开关电源的输入电容承载的电流脉冲也是矩形脉冲电流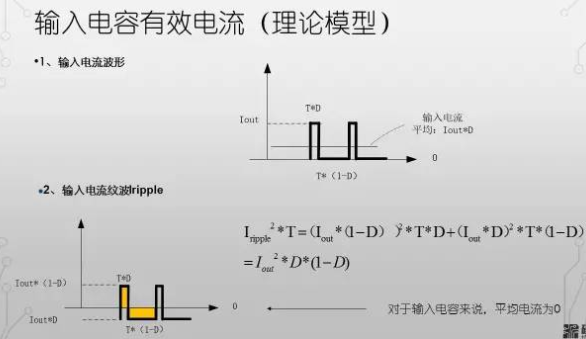

由于在上管打开的阶段，输入电流的大小即可近似的看成输出电流的大小。所以只需要将输出电流的波形叠加在输入电容的波形上面，可以得到上图中的波形。
那么按照有效电流定义，我们可以通过对电流平方在时间上的计算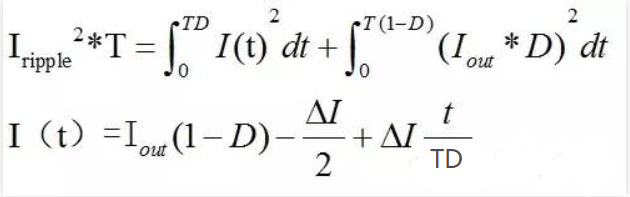

为了简便计算，我们将能量拆成纹波部分，和直流部分。
原先的直流部分，我们直接用乘法进行计算。
直流部分，我们按照近似计算的方法可以得到。
交流部分的功耗，我们按照公式计算可以得到：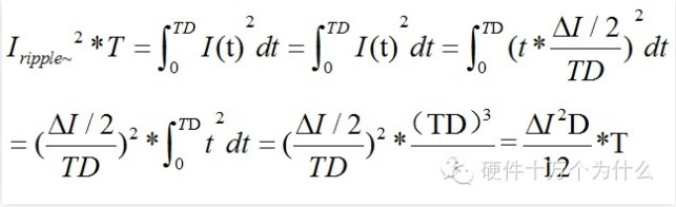


所以总的电容上的有效电流为：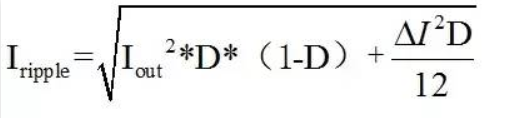

如果选用220uF的电容,每个能承受的有效电流为3.8A。如果我们计算出来输入电容的有效电流值为7A，则需要选用220uF电容2个。高分子电解电容能够承受的有效电流值是有限的。在设计时需要充分考虑电容的承受能力。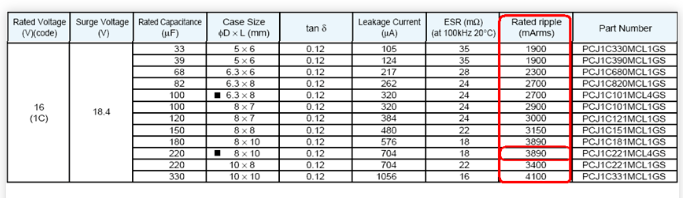

如果没有输入电感，则电容的容值并不是非常重要，可以利用供电电源稳定输入电压值。只要前一级的电源带负载能力够强，应对电流突变的能力足够大（其实也是前一级的输出电容足够多），则电源输入测的电容容量并不重要。
 如果有输入电感，则输入端的电容容值显得重要，影响输入电压值跌落和输入电压纹波，利用充放电的电量相同可得：Q=C*ΔUQ=Iout*T*DC=Iout*T*D/ΔU