EEPW论坛

1.1基本原理

回归用于确定输入变量和输出变量之间的关系，回归模型是表示输入变量到输出变量之间关系的映射函数。回归分析通常分为模型学习和预测两个过程，前者主要根据给定的训练数据集构建回归模型，后者则根据新的输入数据预测相应的输出。

回归模型包括一元线性回归模型与多元线性回归模型，基本形式如下：

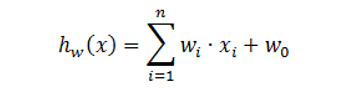
x=[x₁,x₂,…,x_n]，参数w_i(i=1,2,…，n)与w₀分别称为权重系数与常数。

其中，当n取值为1时为一元线性回归模型（即只包括一个目变量和一个因变量且二者之间为线性映射关系)，大于1时则为多元线性回归模型(即包括两个或两个以上的自变量且因变量和自变量之间是线性映射关系)。

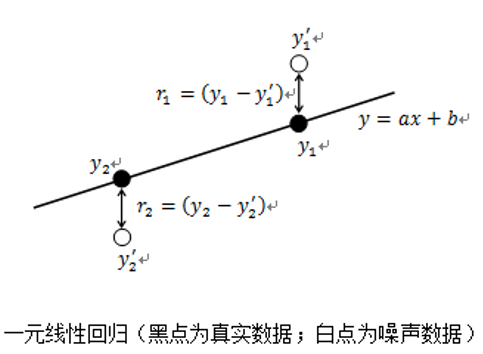
以图所示一元线性回归模型为例,线性回归的目的在于确定一条直线(如y = ax +b）以最小的误差（如r₁、r₂等）的方式拟合数据。在实际中，期望每个点均在该直线上(即r₁、r₂等误差均为0）是难以做到的，因而一般希望每个点尽量离该直线近一些或整体误差最小(即r₁、r₂等误差之和最小)。

1.2求取模型参数

为了求取模型参数a与b，通常可通过以下几个步骤完成:

ü  根据样本集{(x_i,y_i)}(i= 1,2,…,n)，确定平方损失函数R_i(a,b)=(y_i - ax_i-b)²;

ü  构建代价函数L(a,b) = 

ü  通过特定算法〔如最小二乘算法、梯度下降算法等）确定代价函数取最小值时的参数a与b。

1.3编程实现（以最小二乘法确定代价函数）

最小二乘法：将求代价函数L(a,b)最小值的问题就转变成了求极值问题，进而通过求参数a与b的偏导数的方式确定其最优值，即:

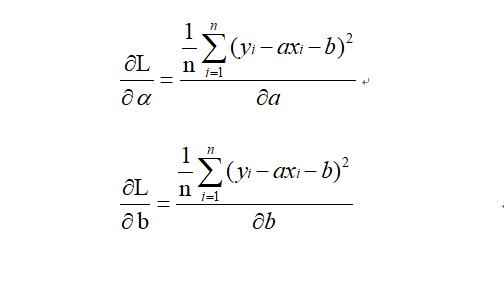
最终解：

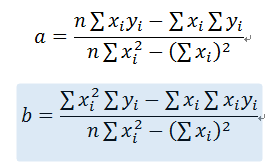
def  LSM(x,y):
    n = len(x)
    sumX,sumY,sumXY,sumXX =0,0,0,0
    for i in range(0,n):
        sumX  += x[i]
        sumY  += y[i]
        sumXX += x[i]*x[i]
        sumXY += x[i]*y[i]
    a = (n*sumXY -sumX*sumY)/(n*sumXX -sumX*sumX)
    b = (sumXX*sumY - sumX*sumXY)/(n*sumXX-sumX*sumX)
    return a,b

1.4习题练习

1.在指定斜率与截距（如k=2、b=5）直线L0上随机采样50个真值点（X0），然后根据X0生成噪声服从正态分布（如均值为1、方差为2）的样本（Xn）。

2.利用Scikit-learn线性回归库拟合Xn以生成拟合直线L1。

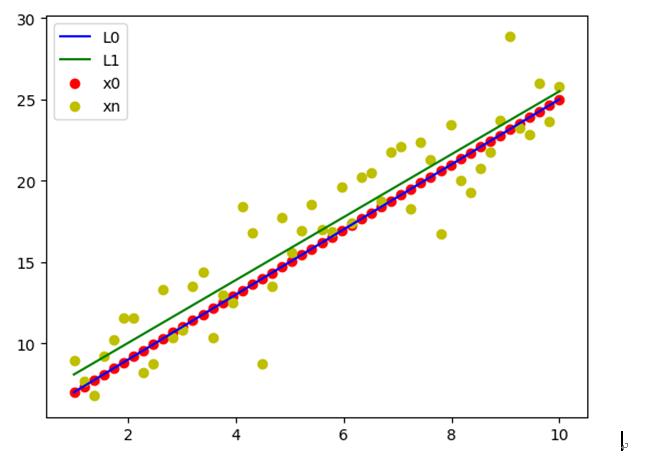
import numpy as np
import matplotlib.pyplot as plt
#1.在指定斜率与截距（如k=2、b=5）直线L0上随机采样50个真值点（X0），
#然后根据X0生成噪声服从正态分布（如均值为1、方差为2）的样本（Xn）。
x=np.linspace(1,10,50).reshape(50,1)
k=2;b=5
x0=k*x+b # 原始点
mu=1;sigma=2
zao=np.random.normal(mu,sigma,50).reshape(50,1)
xn=np.add(x0,zao) #噪声点
# 2.利用Scikit-learn线性回归库拟合Xn以生成拟合直线L1。
from sklearn.linear_model import LinearRegression
lr=LinearRegression(fit_intercept=True)
lr.fit(x,xn)
pre=lr.predict(x)# 预测值
# 3.将X0、Xn、L0与L1绘制在一起以比较其之间的差异。
plt.scatter(x,x0,c='r',label='x0')
plt.scatter(x,xn,c='y',label='xn')
plt.plot(x,x0,color='b',label='L0')
plt.plot(x,pre,color='g',label='L1')
plt.legend()

结果展示：