EEPW论坛

自主导航系统是智能机器人必不可少的一个组成，SLAM所完成的仅仅只是地图构建的工作，在建图的过程当中也有定位的数据输入。

导航系统是移动机器人在已知地图/未知地图的情况下，通过定位算法得知自身在地图的未知，并且在自身位置和目标位置之间做出路径规划并执行的过程。ROS系统中Navigation功能包的move_base框架是现阶段应用最为广泛的内容。

 move base导航框架

在上一个过程已经建立了地图文件，再通过map_server地图服务器加载地图即可获取起始点和目标点的位置信息。

通过地图的权重值，在起始点和目标点之间先做出一条全局的路径规划，这里使用Dijkstra全局路径规划算法即可实现。

在实施全局路线计划去往目标地点的过程中，由于考虑到了地图环境的动态变化特性，在全局计划实施的路径下，可能会存在新的、动态的障碍物，因此须通过局部路线设计程序，在去往目标地点的过程中逐步对环境作出规划感知。

move_base的框架图如图所示，最上面的move_base_simple的geometry_msgs是目标点的数据输入。

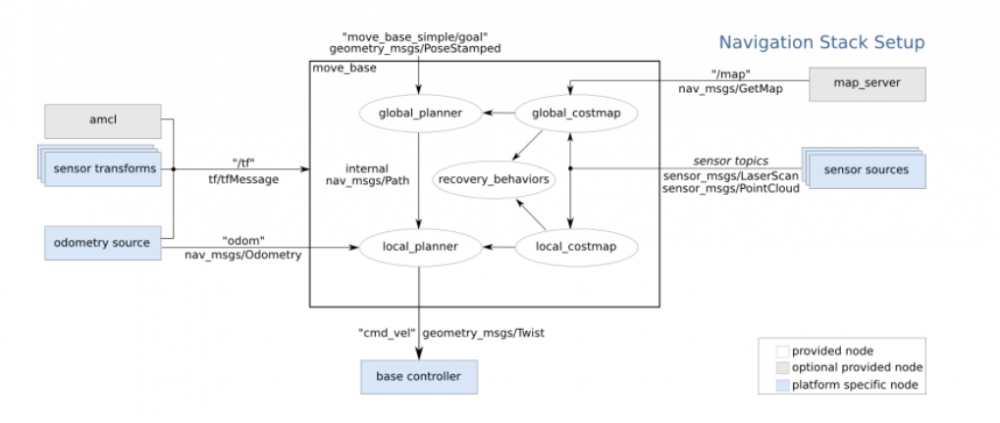
整个框架先从左侧看，需要机器人的位置关系tf和里程计Odom，然后用这两种数据来进行确定，图中的位置算法为AMCL（Adaptive Monte Carlo Localization）的自适应性蒙特卡洛位置。

右上角部分的是map_server加载当前的地图文件，然后计算传感器数据sensor souces的接入，传感器数据可分为LaserScan雷达数据或者PointCloud深度相机的点云数据。

在框架的内部，首先经历的是global_planer全部规划器规划出一条路径，在运动的过程当中再由local_planer局部规划器规划出一条可实时“走”的路线。

在这个过程当中，两个规划分别通过global_costmap全局代价地图和local_costmap局部代价地图来规划设计，其中遇到导航失败的情况(路径下出现障碍物、获取自身位置失败等)会启动recovery_behaviors恢复机制来尝试解决问题。

move_base框架所输出的数据“cmd_vel”到base_controller底盘控制器，从而驱动底盘电机带动机器人运动。

“cmd_vel”输出的是x、y、z三个方向的速度值和角速度值，本文根据设计底盘的情况采用了两轮差分运动学模型。

在move_base框架当中默认的定位算法是AMCL粒子探测定位算法，但是AMCL粒子探测定位的准确度相对较低，而且它是基于2D激光雷达的的定位算法。

目前高校、企业应用主要以多线激光雷达为主，对于多线激光雷达的建图定位算法只有Cartographer和Liom系列。

定位信息数据有TF坐标变换进行维护，其中map->odom->base_link的坐标变换均有Cartogepaher提供，坐标变换关系如图4.10所示。

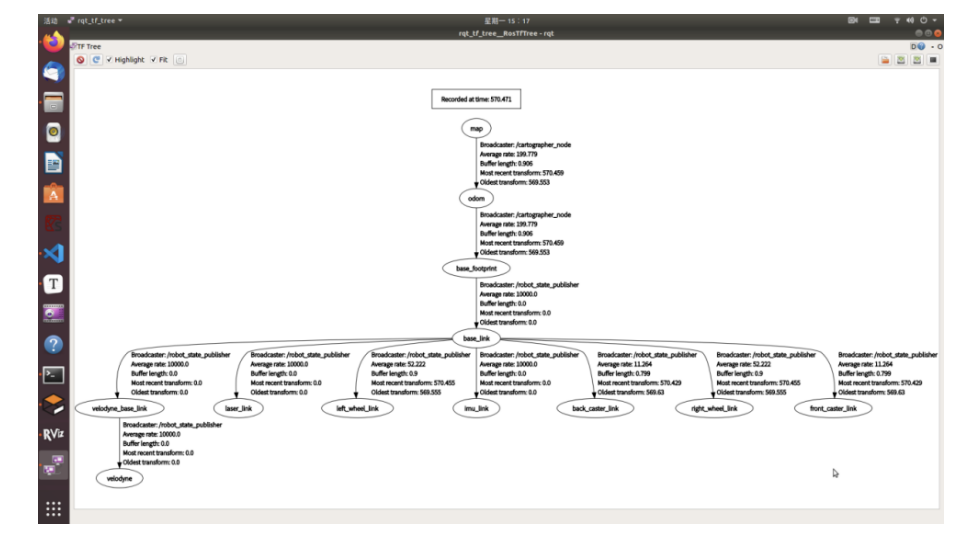
基于Cartographer的TF坐标变换关系

当前定位框架数据关系图如下所示。

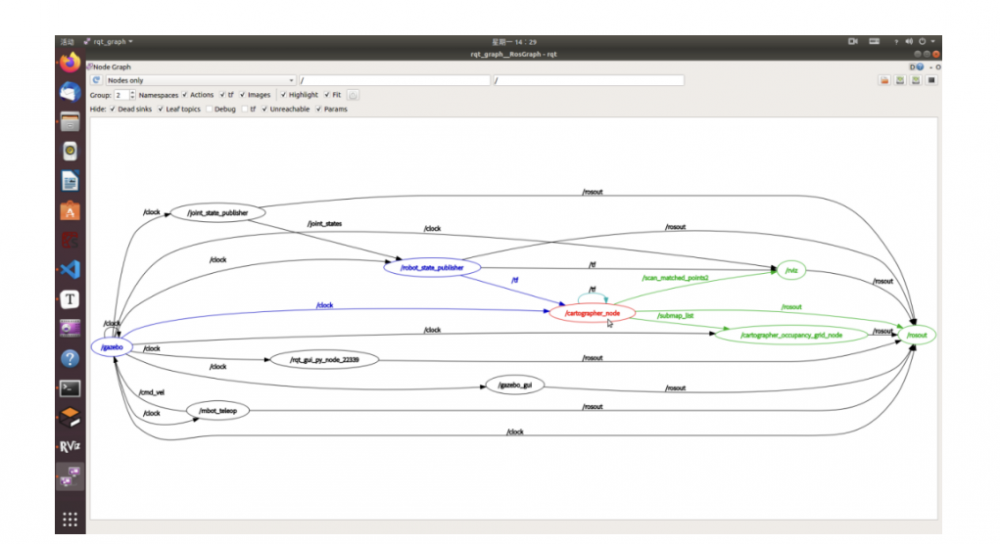
 基于Cartographer的通讯节点关系图

从上图可以分析得到，Cartographer发布submap_list子图队列用于定位，而经过校准生成的/scan_matched_points2作为可视化的数据输出。

全局路径规划器

利用定位算法即可了解自动化机器人当前时刻在地图中的位置，以及如何在当前方位与目标点方位间计算出一个最佳的路线，这对于移动机器人的导航系统也必不可少。这里采用了Dijkstra方法，实现了全局路径计算。

Dijkstra方法由荷兰知名的计算机物理家埃兹赫尔戴克斯特拉(Edsger Wybe Dijkstra)所提供，通过预测从起始点至自由空间内任何一点的最少时间，就可以得到全局的最优化路径。

计算时从起始点出发，先计算周边四个甚至八大一个点至起始点的距离，然后再以新计算距离的某个节点作为计算节点计算其周边一点至起始点的距离，这种运算象波阵面那样在自由空隙里传输，直至到达目标地点。这就能够算得到机器人的最少时间里程。

Dijkstra算法是一个典型的广度优先的状态空间搜寻计算，即计算会从起始点出发逐层逐层地寻找整个自由空间，直至抵达目标地点。

这会增加运算时间和数据量。而且，搜索得到的大量信息对于机器人运动来说是无效的。

Dijkstra算法也算是利用了贪心思想进行的，先将从起始到每个节点的最大距离先记录下来寻找从某个到v的，然后重复松弛一次然后再重新寻找到v的，所谓的重复松方法就是说，再重复遍历一次看通过将刚才找的距离比较短的一个点做为中转站会不会更近，如果更近的话就再调整距离，这样当将所有的节点都找遍了以后，就保留下了从起始到其他每个节点的最短距离。

使用Python编程+Matplotlib数据可视化编程进行路径算法的模拟，在指定起始点和目标点之后，调用定义的Dijkstra类实现路径的搜索规划，最终通过plot类进行可视化显示。

 Dijkstra算法入口功能

入口函数部分先声明起始点和目标点，通过调用Dijkstra类构造实现，通过plotting类进行数据可视化。路径规划的解算在dijkstra.searching()方法来实现，将解算得到的path和visited传入plot进行可视化显示。

Dijkstra算法是依据数据结构的基本构造进行实现，核心代码如图所示。

 Dijkstra算法实现

Dijkstra算法使用的是一个贪心方法，声明了一个数组来保持所有源点和每个顶点之间的最短距离，还有一个保持了那些已经得到的最少路程的所有顶点的集合。

因此还须查看新增加的顶峰是不是能够达到其他顶峰，并且看看经过该顶峰达到其他点的路线长度是否比源点可以径直达到还短，若是即更换该顶峰在g中的值，然后再在g中找到最低位置，然后重复以上动作，直至路线中包括了图的全部顶峰。

Dijkstra算法2D路径规划结果和3D路径规划结果如图所示。

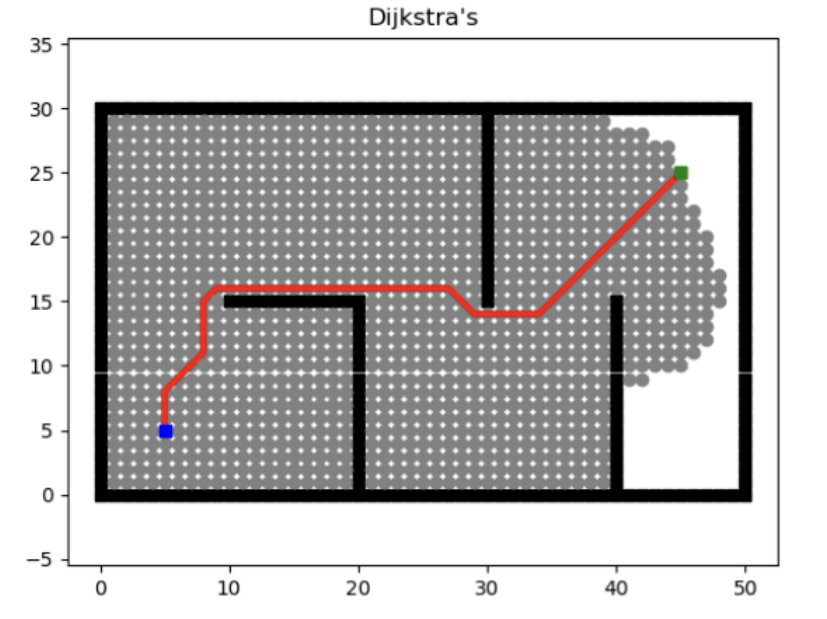
 Dijkstra在2D空间下的路径规划

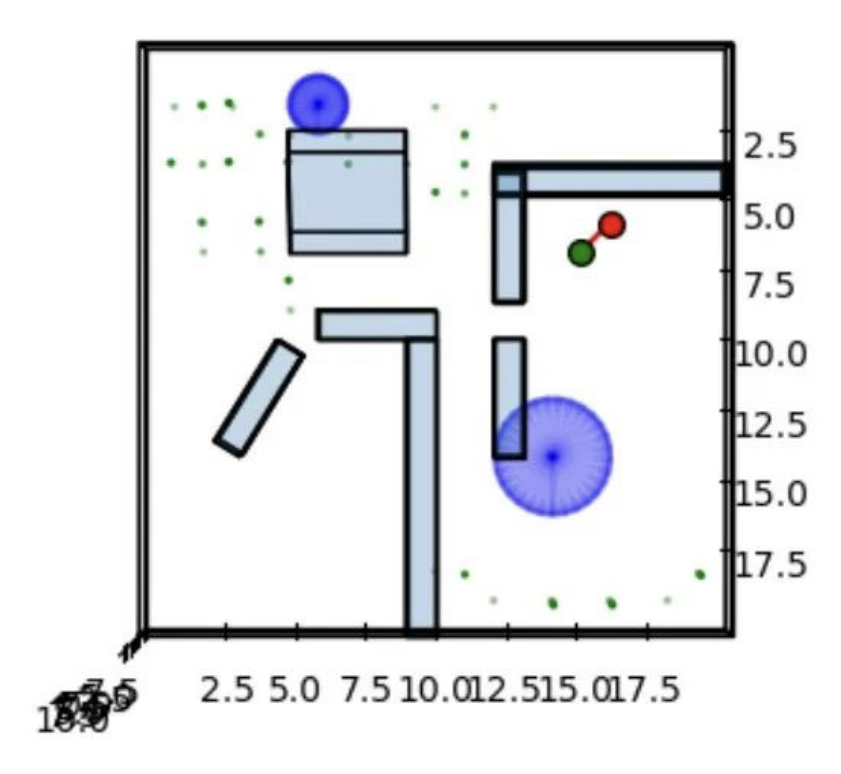
Dijkstra在3D空间下的路径规划