EEPW论坛

下图分析了数字多波束形成器的工作原理：

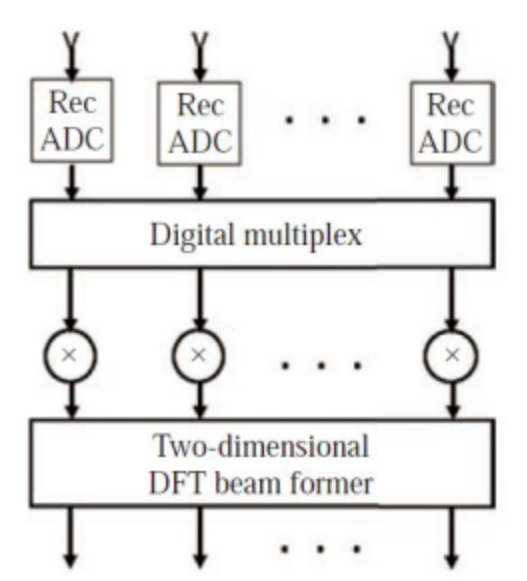
▲多波束数字处理流程图阵列结构可以采取多种形式，而最常见的是矩形阵面，两个维度上的阵元都是均匀分布的。其他的结构包括柱面阵列、共形阵列和非均匀阵列。前端组件包括宽带接收器（每个阵元一个）和带宽为B、动态范围为Nbit的ADC。对于I/Q信号的模拟下变频，每通道两个带宽为B的ADC；对于数字下变频，每通道一个带宽为2B的ADC。每个辐射单元可能包含多个模拟接收和****电路，并将合成后的模拟接收信号输入子阵。对于此操作计算量的估计，考虑阵列结构为均匀的二维阵列，每个阵元包含一个接收器。具有N个阵元（N能被4整除）的均匀线性阵列，可以通过直接傅里叶变换（DFT）进行N个波束的形成，而不需要进行N^2/4次复乘和N^2次复数加法。为了利用DFT算法在方位和俯仰上形成间隔相同的多波束，对纵列进行俯仰DFT计算，实现对俯仰波束的预加权和扫描。俯仰波束已经被预加权，将其转换至方位方向，从而形成N个波束。在一个方形阵列中，每个维度都有N个阵元，N能被4整除，进行预加权和转向所需的复数权重需要进行N^2次乘法求得。此外，还需N^2/4次复乘进行纵向波束形成，N/4次复乘进行方位波束指向。处理单波束的总计算量为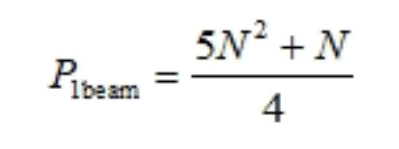： 处理K个波束需要进行的复乘次数为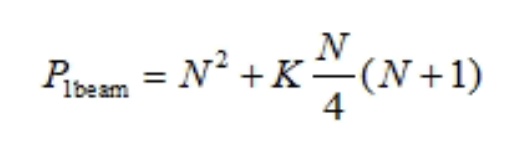：需要指出的是，如果每个方位波束具有相同的俯仰角，那么复乘的次数将减少。下表总结了，对于一个5MHz的采样信号，16x16阵列和64x64阵列的复乘和复数加法的计算量。随着宽带ADC采样率的增加，复数乘法和加法的计算量将成比例的增加。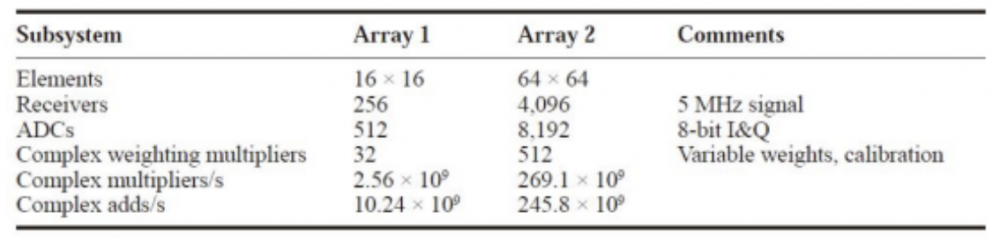▲不同阵列的计算量对比如果两个维度的阵元数量都是二进制数，那么可以采用效率更高的FFT算法。在这种情况下，2^n阶的FFT需要进行N*log2(N)次复数加法和u*(N/2)*log2(N)次复数乘法，其中u是比1小的因子，典型值为1/3。相较于DFT，该方法减少了计算量。然而，该方法需要与DFT相同数量的复数乘法进行预加权和均衡。最重要的一点是，FFT算法能够通过相移进行波束转向。