EEPW论坛

SEARCH-BASED PATH FINDING（基于搜索方法的路径规划）1.图搜索的基本概念1.1 配置空间

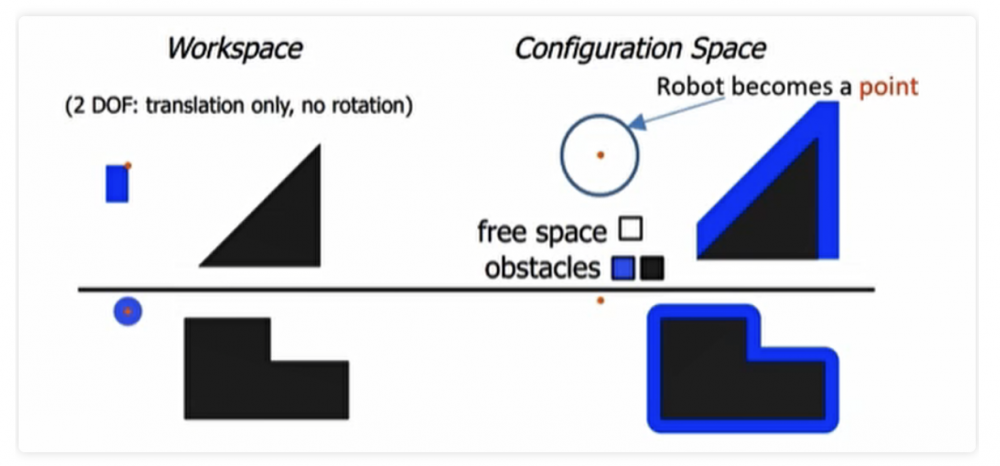
机器人在工作空间中有尺寸，有大小，很难进行运动规划，于是就有了配置空间，将机器人抽象成质点容易进行路径规划。

配置空间：在n自由度空间下包含所有尽可能的机器人配置，又叫C-space。

机器人所有可能的位姿，都在C-space中，用点表示。

1.2 障碍物配置空间

机器人在工作空间中有尺寸、有大小；因为障碍物的碰撞检测需要知道机器人的几何形状，计算时间耗费严重且困难，于是就有了障碍物配置空间。

将工作空间中的障碍物转化到配置空间，将机器人抽象成质点，障碍物加上膨胀（C-obstacle），膨胀和机器人外形尺寸有关。

C-space = C-obstacle ∪ C-free。

在下面学习中的移动机器人的运动规划，就是一个质点在C-free的规划。

1.3图的概念

图有顶点和边。

边可以分为有向的和无向的，又可以分为有权的和无权的。

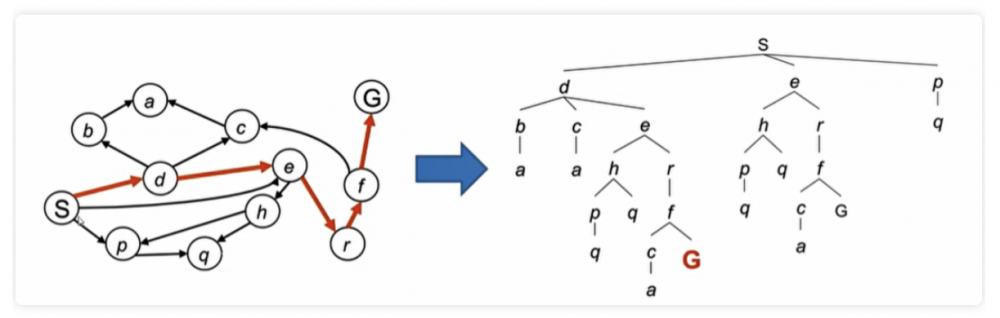
1.4图搜索

图搜索总是从一个起点开始到一个目标顶点。

图搜索总是产生一个完整的搜索树，从搜索树反向跟踪可以得到点到点的路径。

对于很多情况，我们不能完整的构建搜索树，我们只想尽可能快的达到目标顶点。

图搜索整体的算法框架：

（1）构建一个容器，用来存储我们需要被访问的节点；

（2）使用开始节点初始化容器；

（3）循环；

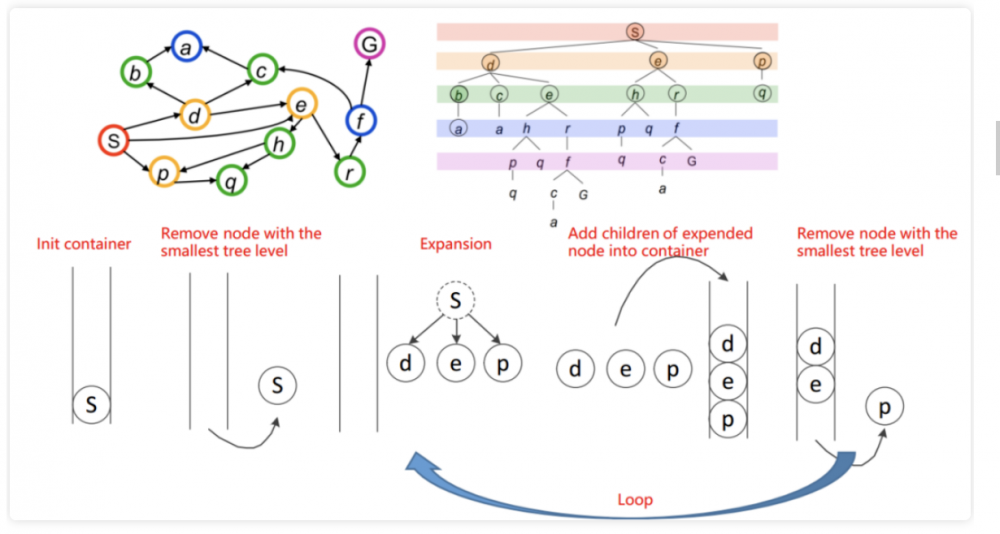
LOOP
 根据某种预先定义的规则从容器中剔除一个节点
 寻找该节点的所有邻居节点
 将所有的邻居节点放入容器
END LOOP

1.5 图搜索算法

深度优先搜索（DFS）：

每次剔除节点遵循先入后出的规则，类似栈。

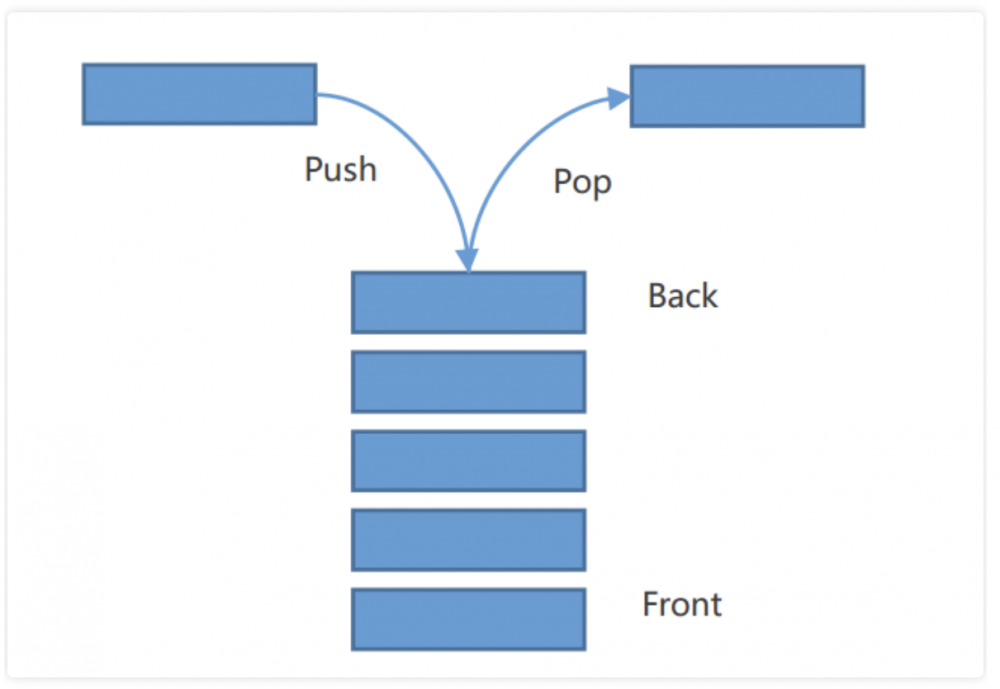
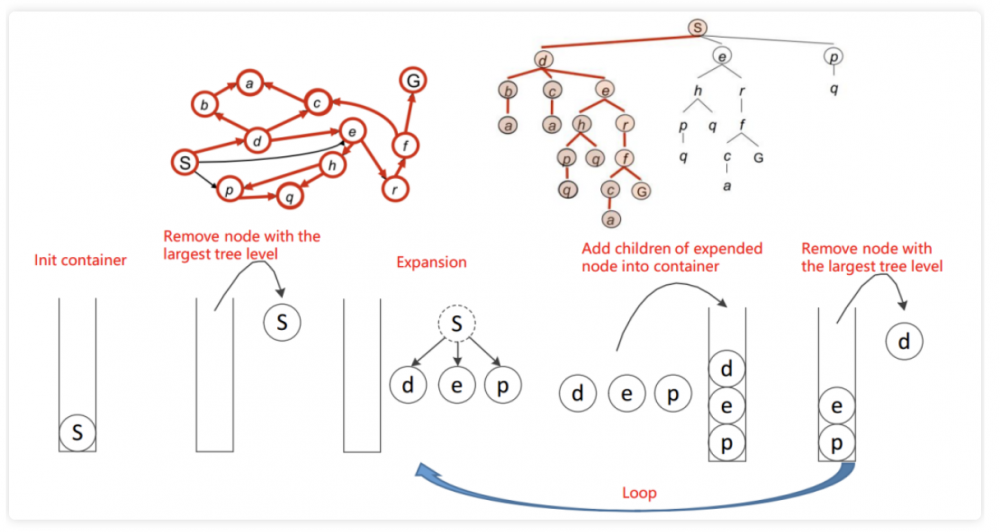
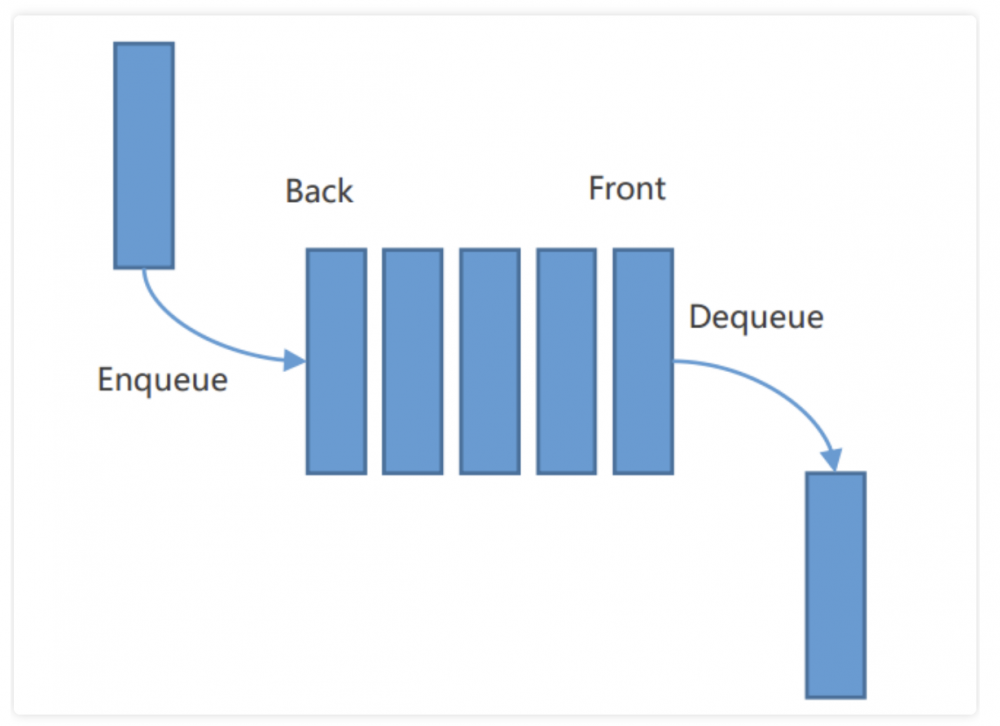
广度优先搜索（BFS）：

每次剔除节点遵循先入先出的规则，类似队列，之后路径规划使用的BFS算法。

启发式的图搜索算法（贪心算法）：

启发式就是对你距离目标有多近的猜测；

启发式指引正确的方向；

启发式应该可以更简单的去计算；

简单概述就是说贪心算法，更急功近利，但是通常也经常获得稍微坏的结果。

1.6 代价的行为

通常情况下，节点之间的联系都是存在代价权重的；

当代价权重为1时，BFS可以找到最优解；

然而，对大多数时间，节点之间的代价并不为1，且是复杂多变的；

所以依托BFS，也就出现了传统的最短路径的图搜索算法。

2.传统的Dijstra和A*算法2.1 Dijkstra

与之前BFS唯一不同的地方：通过最低累积代价函数g(n)进行拓展和访问节点，即是踢出节点的规则。

代价函数g(n)：从起始节点到n节点的累积代价值的当前最优值；

更新节点n未被拓展的邻居节点m的累积代价g(m)；

一个被拓展或者访问过的节点保证从起始节点开始有一个最小的代价。

伪代码流程：

算法好处：完整和能计算出最优解。

算法坏处：一层一层的探索代价、没有对目标位置的信息。

2.2 引出启发式搜索

通过使用猜测到目标点的最小代价来克服均匀代价搜索的缺点；

即引出，A* = 带有启发是搜索的Dijkstra。

2.3 A*

累积代价：g(n) 从start到n节点的最小累积代价；

启发探索：h(n) 从节点n到goal的最小估计代价；

通过n节点估计start到goal的最小估计代价函数 f(n)=g(n)+h(n)；

也就是说，我们拓展节点的策略是：拓展最小f(n)的节点。

伪代码流程：

A*算法解的是最优解吗？

通常不是，除非h(n)=0，此时算法退化为Dijkstra将得到最优解；

如果不对h(n)限制的话，将会出现h(n)>h*(n)的情况；

可允许的启发探索（admissible）；

一个h被允许的条件：

对于所有的节点n都存在h(n)<=h*(n)

*h(n)**是从节点n到goal的真实最小代价

所以如果h(n)是可被允许的，A*的结果就是最优的

所以A*在实际使用时，提出一个可被允许的h是占比重比较大的一部分

h的设计

可以参考的例子

欧氏距离  总是可行的  机器人在栅格中走x、走y、走xy对角线

曼哈顿距离 如果机器人走xy对角线时，不可行，只走x，y时，可行的

0距离 总是可行的

无穷范数距离总是可行的

Dijkstra和A*的比较

Dijkstra拓展朝向所有方向

A*的拓展朝向目标，仍然可以确保是最优的，因为有合理的h启发函数

2.4 次优的求解

如果我们使用过度估计的启发式函数呢？

次优的最快路径 ==》权重的A*

weighted A*

牺牲最优性，换取速度上的提升，几十倍的速度提升

2.5 基于栅格路径搜索的例子2.5.1如何将栅格地图表示成图？

每一个栅格都是一个顶点，边连接着相邻的栅格。常见4连接、8连接

2.6 最好的启发式函数选择2.6.1 问题的提出

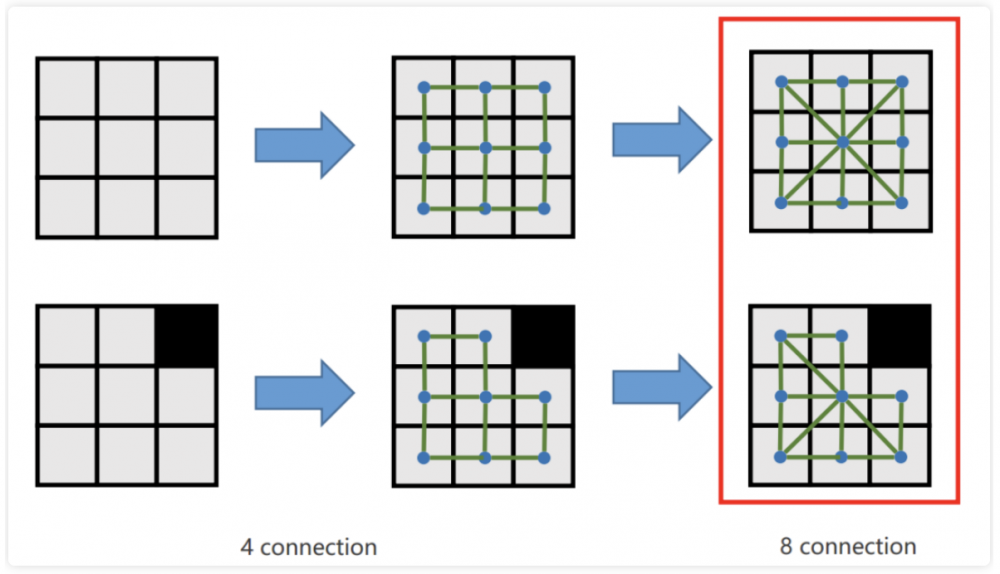
之前提到的启发式函数设计的例子，远远不满足现实的要求，比如启发式函数使用欧式距离的方式，拓展了许多我们不需要的点

因为此时的h(n)<<h*(),我们不允许这样的事情发生

2.6.2 如何计算真实理论的最优解

2.6.3 打破平衡(加快计算速度、减少不必要的节点访问)

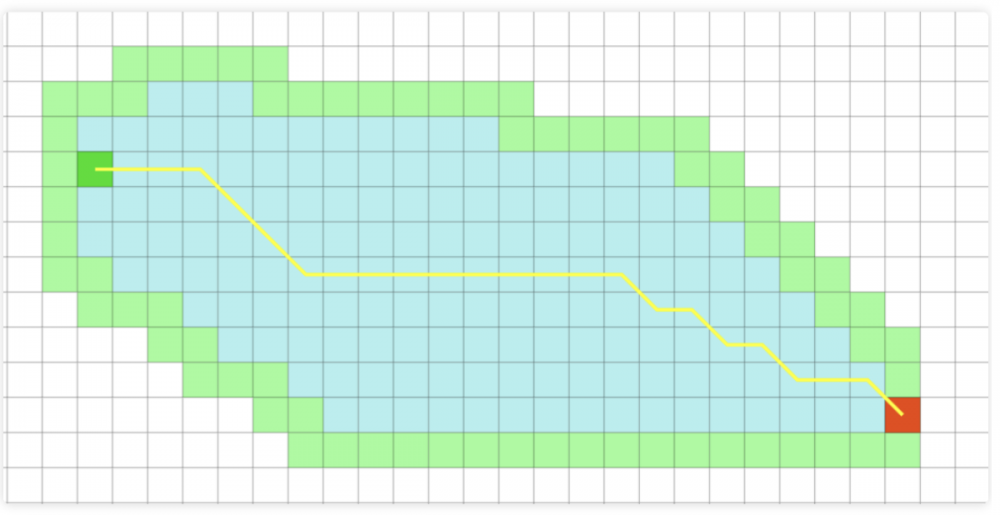
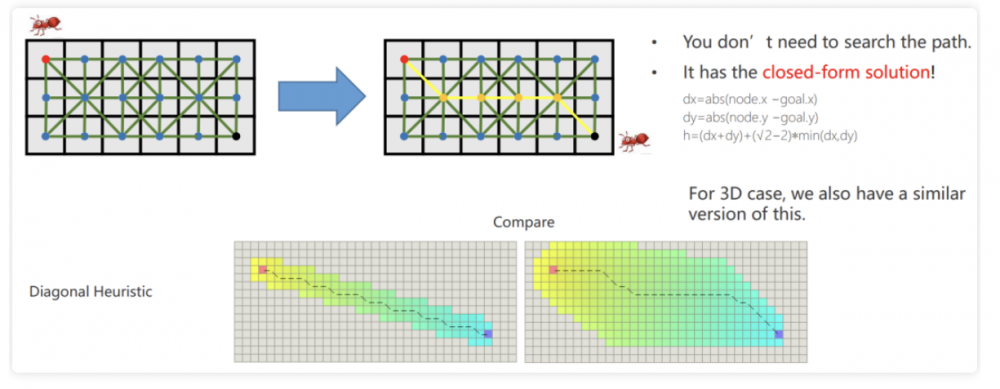
核心思想

对相同代价f的path的h进行改变，以至使平衡被打破。（可以理解为使得没有两个相同代价f的路径）

why？

许多路径都有相同的值，它们之间没有差异，以至于使得A*算法对它们平等的探索，所以出现了上图过多的点被访问的结果。

打破的方式

第一种做法：

将具有相同f的路径的h稍微的进行放大。虽然理论上存在h是不可行的，但是在实际的应用中几乎没有影响

第二种做法：

当节点有相同的f时，比较他们的f大小，根据大小做选择。

很多其他方法...

3.跳点搜索算法（Jump Point Search）

系统性的打破路径平衡的路径搜索算法

3.1 JPS的核心思想

JPS基于A*算法，系统的解决路径的平衡问题

JPS依靠某种规则向前看，选择所有对称路径中的一条

3.2 向前看的规则

该规则的目的：对邻居进行裁剪，（pruning）,我们根据该规则抛弃一些不需要访问的节点，将需要访问的节点放入open list中

3.3 跳转的规则

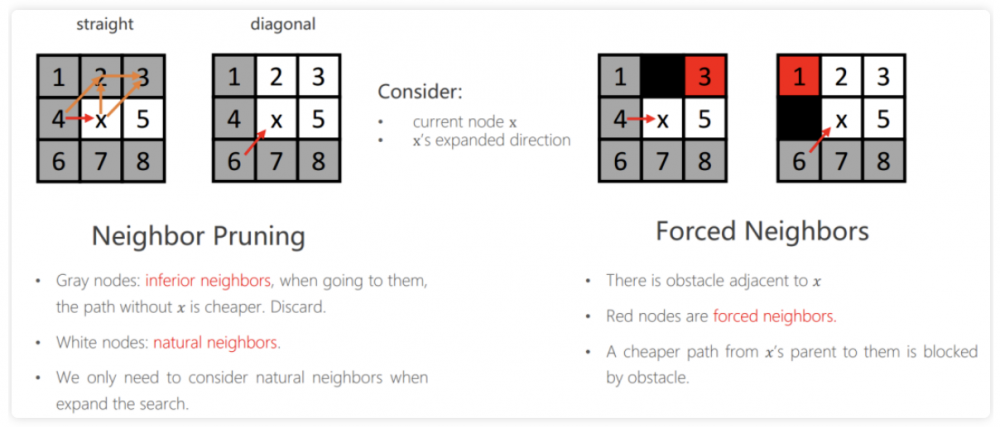
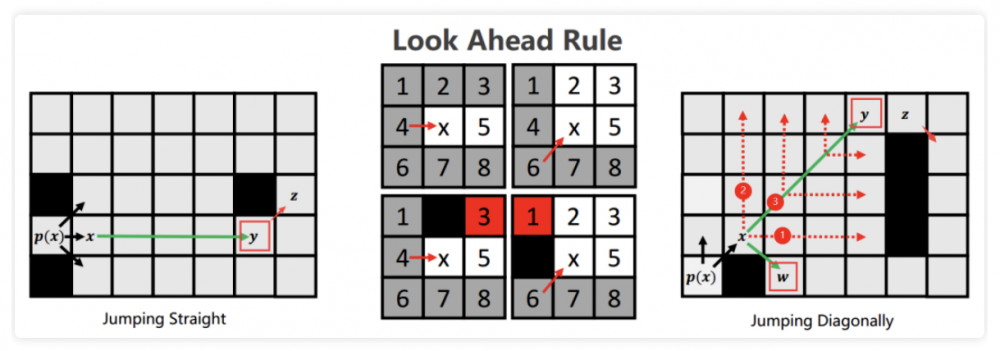
方式一：直线跳转，遇到特殊标志的点作为跳转选择点

方式二：对角线跳转，先两个方向的直线跳转，如果都迭代失败，对角线走一格，重复直线跳转，直到在直线跳转的地方发现特殊标志的点

将上述所说的跳转点，纳入到open list中，特殊标志起始点周围的w也需纳入到 open list 中

3.4 伪代码（与A*的区别）

整套算法仅仅只是选择节点放入open list的规则不同，代码没有什么本质的区别

3.5 图示算法流程

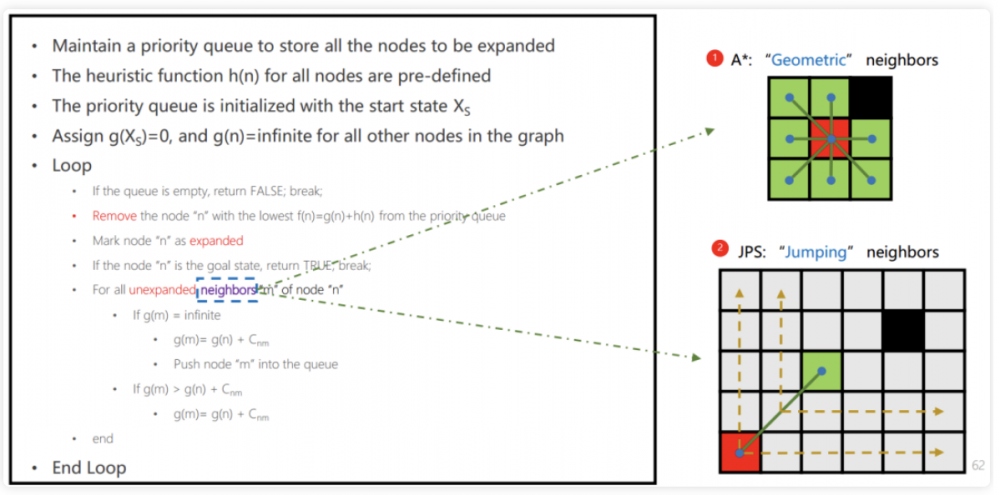
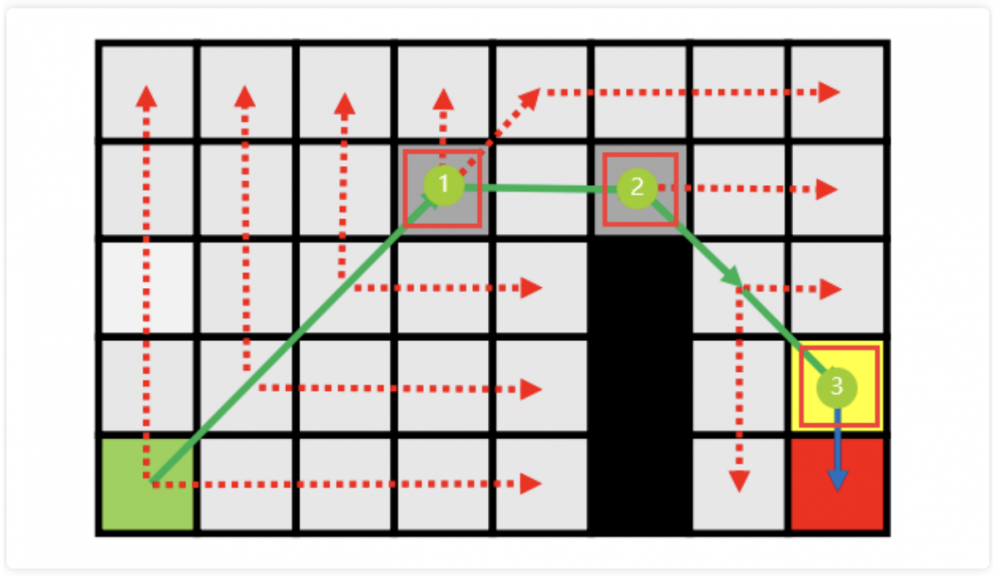
过程：

（1）首先，将发现关键节点1，放入openlist，继续走对角线，探索失败

（2）将节点1从open list 弹出，走直线，节点2 为特殊选择点，将节点2放入 open list 中，探索失败，走对角线（方向有讲究）

（3）走直线探索，失败，走对角线、走直线探索，失败，直到发现目标点或者关键选择点，发现关键节点3，将节点3放入open list中

（4）将节点3从open list 中弹出

3.6 JPS的优势与不足

在复杂的环境中，JPS效果往往较好。若是在极度空旷的环境下，JPS的效果十分不好。