EEPW论坛

这篇讲的比较好，所以贴出来，之前有讲过BOOST电路设计.

以下是对开关电源控制器MC34063的详细介绍：

一、基本信息

MC34063是MOTOROLA公司生产的一款简单耐用的开关电源控制器，其电路设计成熟，且网上有很多典型的例子可供参考。

该芯片内部包含温度补偿带隙基准源、一个占空比周期控制振荡器、驱动器和大电流输出开关，能输出1.5A的开关电流。

二、主要特性

输入电压范围：2.540V（也有说法为3.040V）。

输出电压可调范围：1.25~40V。

最大输出电流：1.5A。

工作频率：100Hz~100kHz。

工作温度：0℃~70℃。

具有低静态电流和短路电流限制。

可实现升压或降压电源变换。

三、引脚及封装

MC34063主要封装有DIP-8以及SOP-8两种，一共有八个引脚，各引脚功能如下：

1脚（SC）：内部开关管Q1集电极C极引出端。

2脚（SE）：内部开关管Q1发射极E引出端。

3脚（TC）：定时电容CT引出端，调节电容大小可使工作频率在100~100kHz范围内变化。

4脚（GND）：电源接地端。

5脚（COMP）：比较器反相输入端/输出电压取样端，使用时应外接两个精度不低于1%的精密电阻。

6脚（VCC）：电源接线端。

7脚（IS）：与振荡器相连接，峰值电流取样端；6脚和7脚之间电压超过300mV时，芯片将启动内部过流保护功能。

8脚（DC）：内部开关管Q2集电极C引出端。

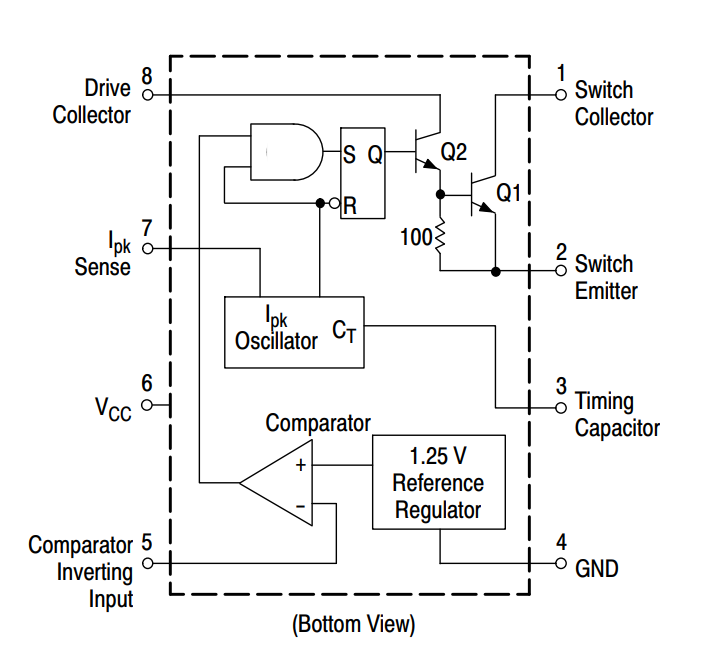
四、工作原理

MC34063的工作原理如下：

降压电路原理：

比较器的反相输入端（5脚）通过外接分压电阻R1、R2监视输出电压。输出电压Uo=1.25(1+R2/R1)，仅与R1、R2数值有关，因为1.25V为基准电压，恒定不变。若R1、R2阻值稳定，Uo亦稳定。

5脚电压与内部基准电压1.25V同时送入内部比较器进行电压比较。当5脚电压值低于内部基准电压（1.25V）时，比较器输出为跳变电压，开启R-S触发器的S脚控制门。R-S触发器在内部振荡器的驱动下，Q端为“1”状态（高电平），驱动管T2导通，开关管T1亦导通，使输入电压Ui向输出滤波器电容Co充电以提高Uo，达到自动控制Uo稳定的作用。

当5脚电压值高于内部基准电压（1.25V）时，R-S触发器的S脚控制门被封锁，Q端为“0”状态（低电平），T2截止，T1亦截止。

振荡器的Ipk输入（7脚）用于监视开关管T1的峰值电流，以控制振荡器的脉冲输出到R-S触发器的Q端。

3脚外接振荡器所需要的定时电容CT，电容值的大小决定振荡器频率的高低，亦决定开关管T1的通断时间。

升压电路原理：

当芯片内开关管（T1）导通时，电源经取样电阻Rsc、电感L1、MC34063的1脚和2脚接地，此时电感L1开始存储能量，而由Co对负载提供能量。

当T1断开时，电源和电感同时给负载和电容Co提供能量。

电感在释放能量期间，由于其两端的电动势极性与电源极性相同，相当于两个电源串联，因而负载上得到的电压高于电源电压。

开关管导通与关断的频率称为芯片的工作频率。只要此频率相对负载的时间常数足够高，负载上便可获得连续的直流电压。

五、典型应用

MC34063能使用最少的外接元件构成开关式升压变换器、降压式变换器和电源反向器，可广泛应用于远程及数据通讯、计算机、自动化设备、工业仪器仪表、航空航天、老人手机、USB小电风扇、电动牙刷、BT蓝牙音箱、可充电键鼠等产品中。

六、MC34063功能介绍

MC34063芯片结构图：

升压电路的典型设计

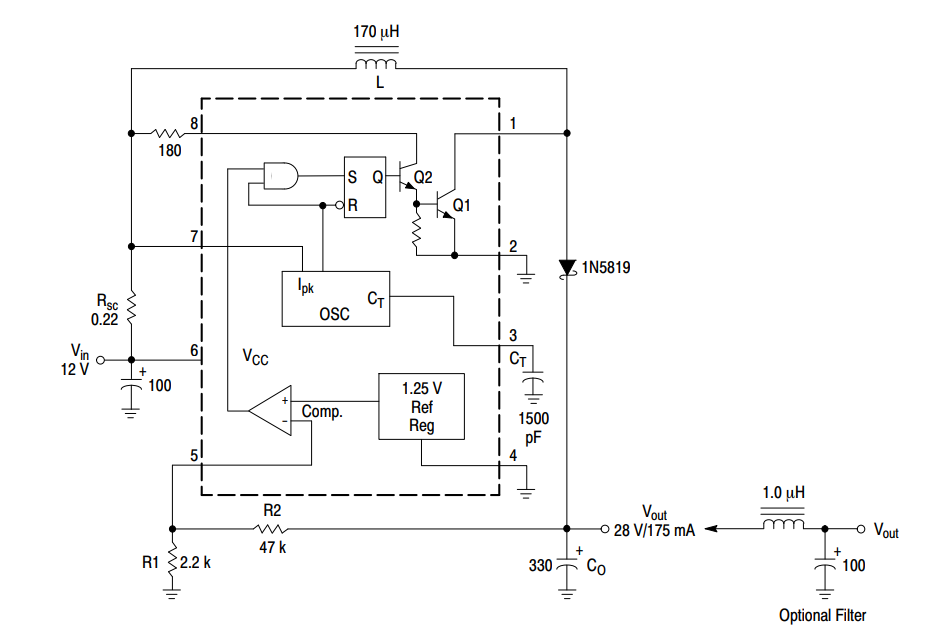
如图是一种典型的升压（boost，step up）设计，芯片的输入12V电源，在达林顿管开启时，电源向电感充电，当电感上的电流达到最大值时（这个值是根据负载环境人为设定的，在后续的峰值电流控制方法中将会提及），达林顿管关闭，此时电感向储能电容供电。

达林顿管开启和关闭过程中的能量守恒当开关开启时，电流在电感中建立，该过程在电感不饱和且严格线性的情况下，电流随时间匀速增加，因此，当达到最大电流图片时，电感中的能量为：

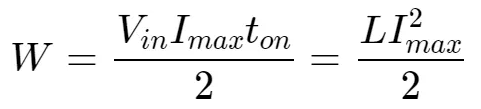
对于输出端，在关断时刻，电流将逐渐下降为0，电感此时释放全部能量到电容，此时电感将释放W的能量到储能电容端。设输出端电势为图片，则在输出端可以将能量W用输出电压及输出电流的形式（“流入”电容的电流）

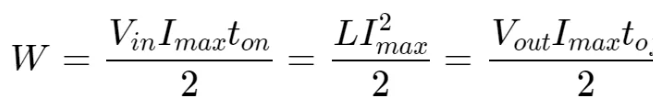
该式子与第一节利用点单的楞次定律推导的结果一致但是亦有不同，这两个式子更为形象，它表明，当电感输出端与储能电容上的电压钳位时，来自电容的电压会阻止电感上的电流流动（注意不是电感上的感应反压，该反电动势只有非钳位情形才有），如果不对占空比进行控制，则当电流减小到0后只能一直维持0电流，直到下一个开关周期开始对电感充电。

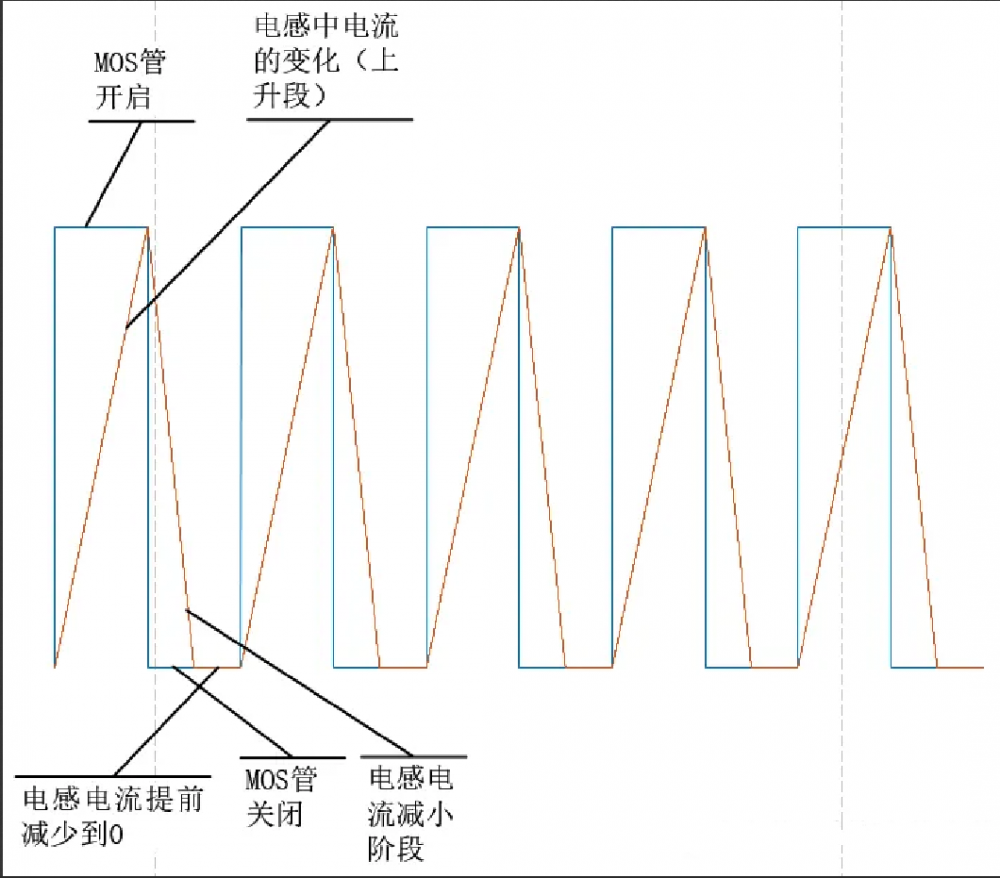
电感电流的变化情况（这里假定电流最终减少到0）因此，由于输出电压较高，则由于该电压作为电流的反压抑制电流流动，一定程度上会使电流迅速减少至0，因此即使不控制占空比也能使电压升高（或者说是输入输出决定了占空比）本例中，当输出达到稳态时，按照比较运放comp虚断原理，则输出电压与参考电压之间有如下关系（）：

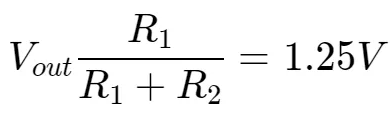
因此只需调整R1,R2的阻值即可获取任意输出电压。本例中，带入阻值可以获得输出电压为27.9545V，datasheet给出结果为28V实际为工程方便而给出的参数。

峰值电流控制已经了解到，即使不对占空比进行控制，电压依然可以得到提升。那么，对于电感后级的储能电容而言，该电压上升的原理又是什么呢?我们知道，电容上的电压取决于电容上的电荷，即：

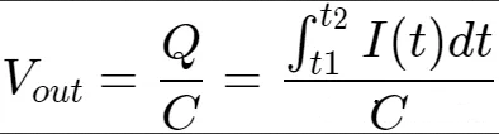
Q:电容两端的电荷差异量（库伦：C）；C：电容（法拉：F）；I(t）：电流随时间的量（安培：A）；t1：MOS管关断时间点；t2：电流减小至0时间点。

如果按照该方程，那么输出电压将呈现一条二次函数曲线，这样与实际输出电压成直流有巨大的区别。

但是事实是，电感向电容释放电流的过程是一个周期二次函数，又傅里叶级数知，该周期函数至少可以分解为其周期函数的基频正余弦函数和倍频正余弦函数的加权和，而电感电容组成了一个通频带极窄的一个低通滤波器，该滤波器将交流信号基本滤除，只留下直流电压，因此输出电压为一个直流信号，因此之前所论述的输出电压被钳位的理论依然是正确的且也和式1不冲突。

即在升压电路中，电感通过周期性电荷充电使电压升高，所以这种电路还有个名称叫“电荷泵”。如果一个周期不行那就多个周期，直到满足闭环控制回路输出的要求。

在建立了电荷充电能够使电压升高的概念后，现在可以引入峰值电流控制了，所谓峰值电流控制就是当电感上的电流达到一定的值时，将电感关断，此时这些电流将流入电容。

升压电路在图中，作为取样电阻，当电感电流增加时，流过取样电阻的电流增加，两端的电压增加，通过检测该电压值即可知道电流的大小，进一步对最大电流进行控制。

峰值电流控制的稳定性分析

在一个开关周期内，当电感充电时间小于等于放电时间，此时电感在关断期间必然使电流减小到0，或直接由伏秒平衡得出。

这里在matlab环境下搭建了一个仿真模型，该模型的主要结构框图如下：

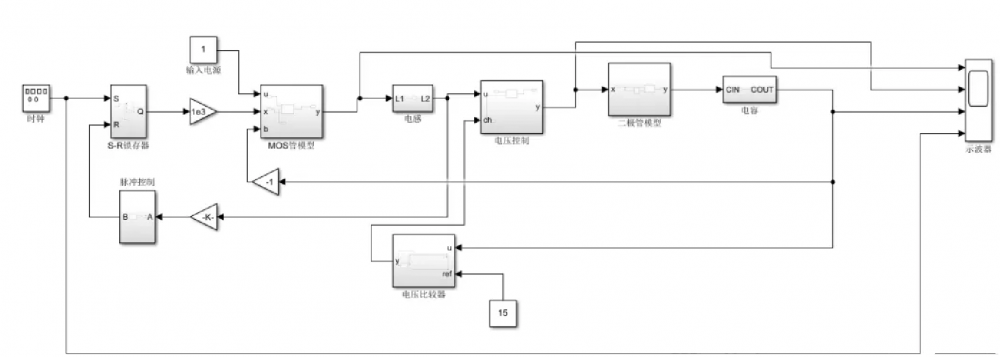
MATLAB电流控制模型

该模型以1V输入并将电压升至15V，该模型包括两个环路，内环为电流环，外环为电压环，由于，电压环负责电路的精确比较，电流环负责对电感充电和放电。其中SR锁存器负责形成电流开关控制，关于SR锁存器的工作原理请自行搜索，这里仅做如下解释（当R为高电平时，Q为低电平；当S为高电平且R为低电平时，Q为高电平；当S和R均为低电平时，电路处于保持状态即电路初始状态初始为高电平则此时仍为高电平，初始为低电平此时仍为低电平）。

脉冲控制模块：当输入大于某个门限时，置高电平，否则置低电平；

电压比较模块：用于和参考电压做比较，当参考电压大于输出电压（u）时，y为低电平，否则为高电平；

MOS管模型：当输入x是高电平时，y与输入电源相连（充电），否则与b相连（放电）；

电压控制：当ch为高电平时，y与u相连（允许电感充放电，或者允许振荡器震荡），否则y=0；

二极管模型：在电流下降沿对后级电容充电。

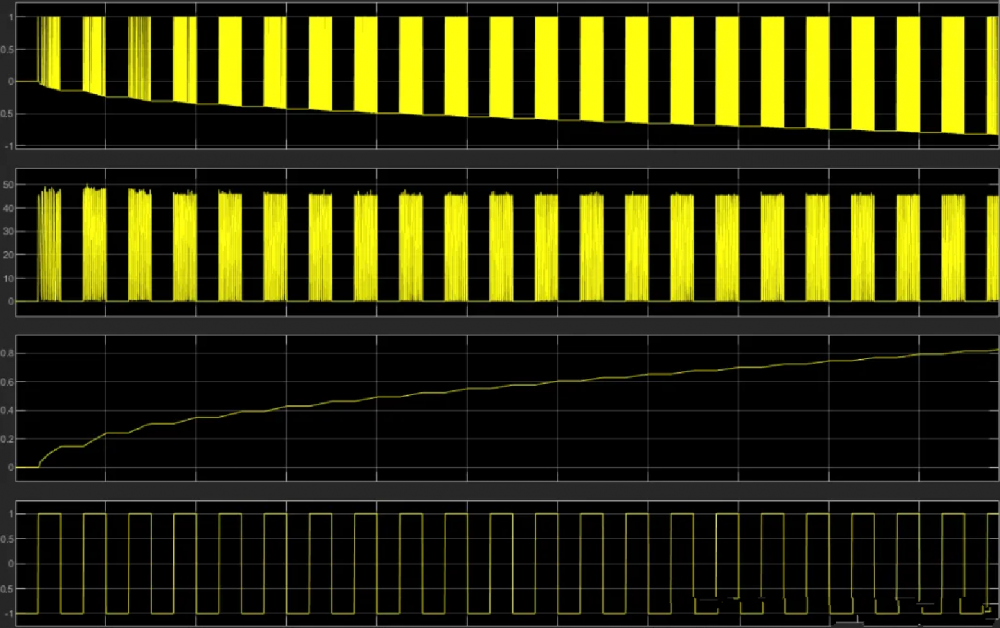
示波器用于观测模型中的输出信号。如图是示波器的波形图：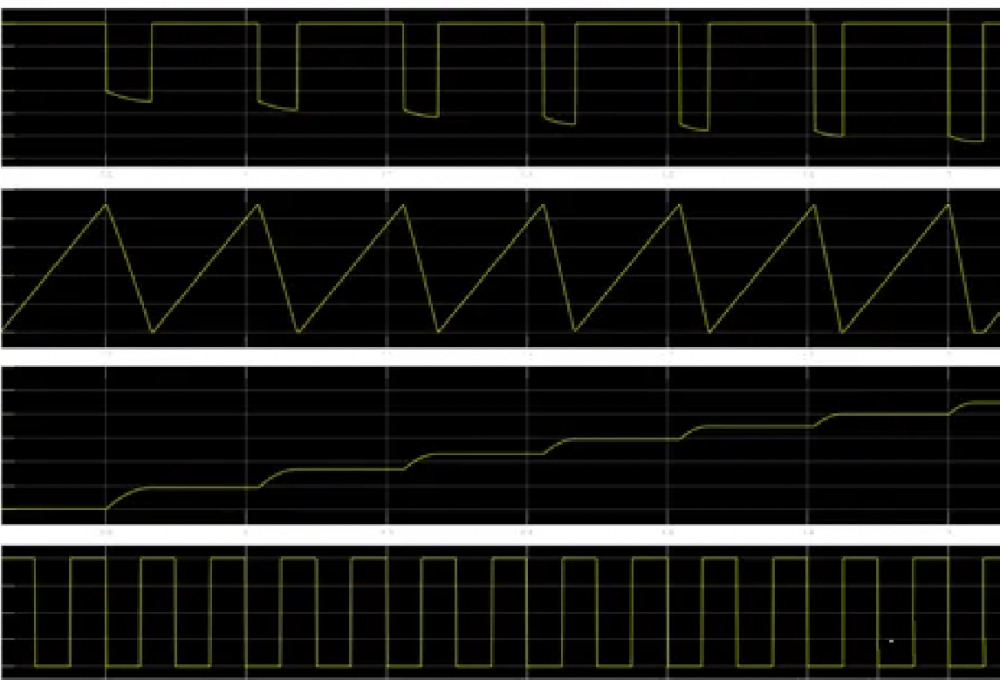

示波器波形图

第一栏为电感上的电动势变化，注意看图中的电压单位负反馈环节，该环节用于模拟反向充电，可以看到高电平为1V低电平逐渐往负方向移动。

第二栏为电流的波形图，第三栏为输出电压的变化，第四栏是时钟信号。

可以看到，仅在电感电流下降阶段对电容充电，且这样的下降沿逐渐增大，因为反压增加的缘故。

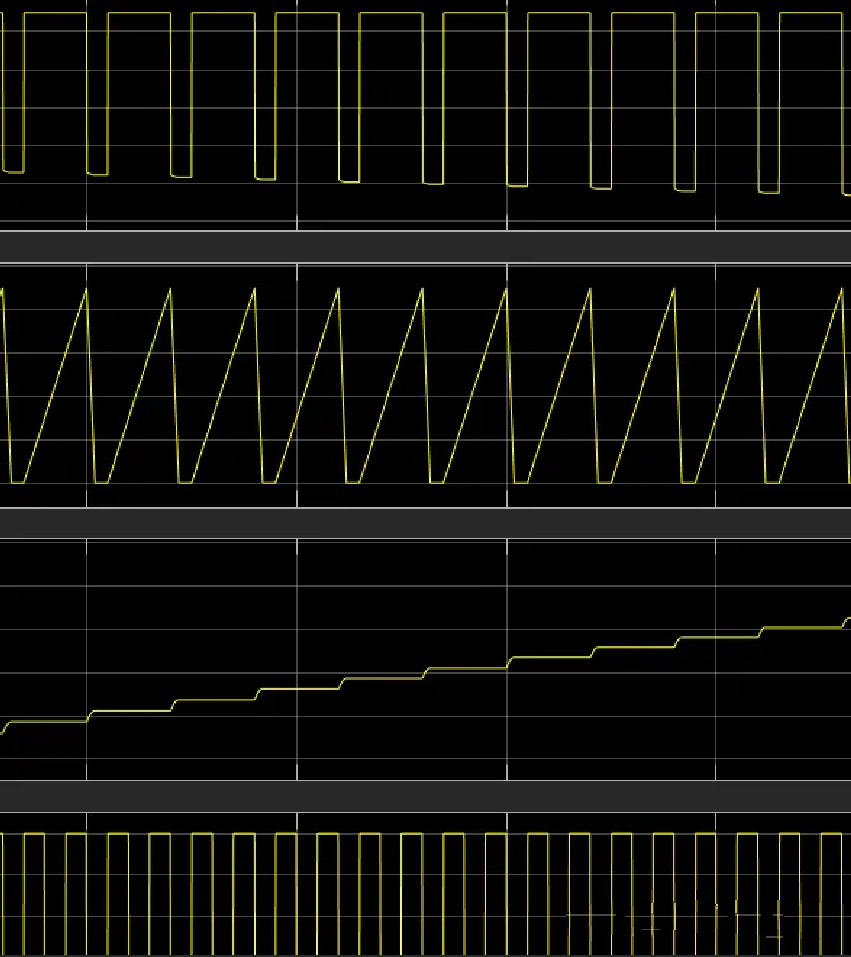
电流下降沿斜率增加

全局充电时序

可以看到，当输出电压达到15V时，电感停止跳动，剩下的时序不做参考。

网上有很多关于峰值电流控制的稳定性分析的文章，但是我想说：任何脱离环路去直接分析开环传递的稳定性都是没有意义的，而网上偏偏充斥着大量的这种文章（不是说它不合理，而是它解释起来很“抽象”）

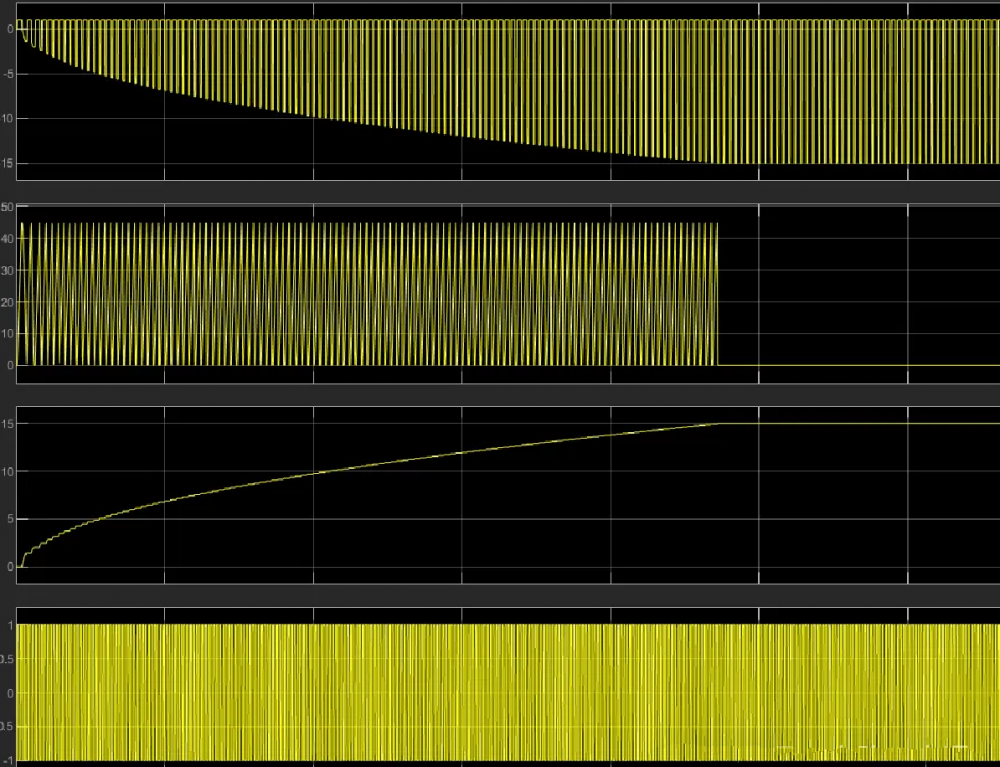
这里，我将电感减少到一定程度（电流增益增加）来解释环路震荡（不稳定的一种表现）图6很形象地阐释了该种情况，可以看到模型出现了大量的高频震荡。

这是由于环路增益变大了导致环路失稳，关于环路稳定和奈奎斯特稳定判据有关，下期我们阐述这种判据的原理及图6波形的来源。

电感减小（电流增益变大）时震荡的图

（MC34063峰值电流控制2）

对自动控制原理有一定基础的，没有该基础的也不用担心，我会用短短的几个词来说明自动控制原理干了些啥。

何为自动控制简单地来说，就是将你的意思让执行机构执行，并且及时获得该执行的情况，大概就是这个意思，如图：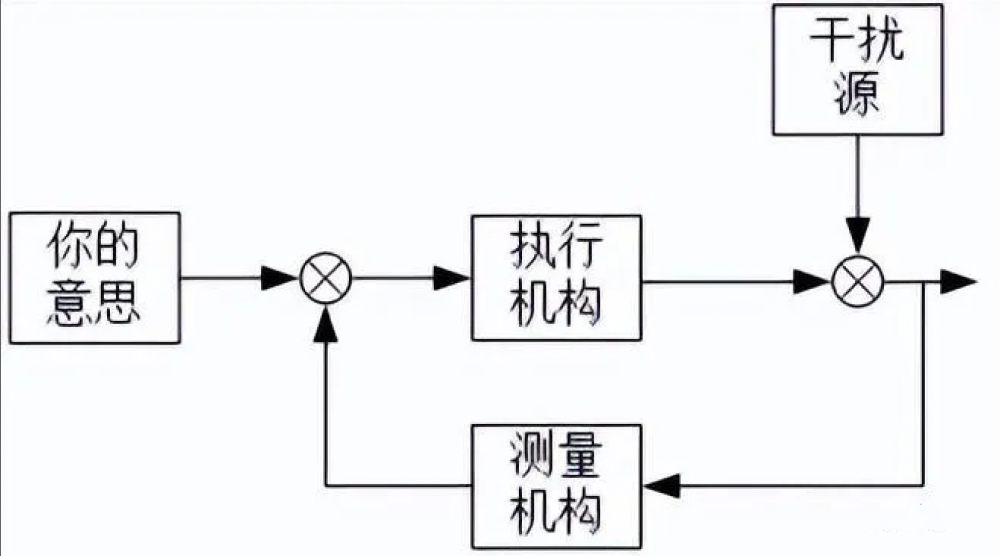

自动控制的结构

这里是一个比较形象的框图了，大概是一些管理学上的问题，即一个老板要看公司的效益好不好，首先会让产品经理提要求，然后员工去执行要求，效果如何应该是测量结果说了算，测量结果如同单位老板的顺风耳，他如实反映员工执行的效果的话，则员工的输出很稳定，但是如果他乱来，可能会让员工崩溃，导致生产混乱。

当然这里只是说其中一个场景，事实是执行机构乱来，也会导致系统混乱。

但是可以肯定的是，外加的干扰和你的意思都是一种输入，外部输入只会引起干扰，如果系统本身是稳定的那么干扰迟早会被消除。

以上这个例子很形象地说明，一个系统能不能正常执行输入的指令，能不能稳定工作，并不取决于高层的意思，也不取决于外部干扰，而是系统内部闭环的情况能不能做好。

正如一个公司，如果人和人之间能好好沟通，不那么勾心斗角，都自觉行使自己的责任，那么高层的指令必然很能贯彻，外接的干扰也必然容易消除。

反面而言，想要破坏一个系统，必然先破坏这个系统的内部，使他们失去协作的能力。

环路稳定与奈奎斯特（nyquist）判据

1中我们已经看到，一个系统稳定性与否只与系统环路有关，伟大的nyquist判据应运而生，这里我不去分析那些复杂的公式，仅感性地说明为何nyquist为何是一个很好的判断系统稳定性的工具。

这里首先说明，线性定常系统时域-频域变换仅取决于系统的参数，而不取决于输入信号。这里先以一个简单的案例来说明问题，如图：

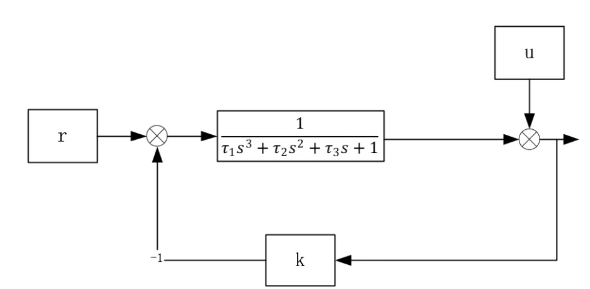
一个三阶系统例子r为系统的输入，u为外界干扰，k为一个测量反馈，现在用环路分析来分析该系统的稳定性：该系统的环路增益为：

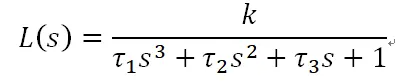
有了以上基础，现在开始看视频吧！总共两个视频，为我搭建的matlab模型，第一个旨在说明环路稳定的机理，第二个旨在说明电流模式下的可能的震荡，当然还有很多震荡模式。

总结：

MC34063是一款功能强大的开关电源控制器，由MOTOROLA公司生产，具有简单耐用、电路设计成熟的特点。该芯片内部包含多个关键组件，能够输出高达1.5A的开关电流，适用于升压或降压电源变换。其引脚功能丰富，封装形式多样，便于在不同场合下应用。

在升压电路中，MC34063通过控制开关管的导通与关断，实现电感的储能与释能，从而输出高于输入电压的直流电。

通过外接分压电阻和比较器，可以精确调节输出电压。此外，MC34063还具有峰值电流控制功能，能够进一步提高电路的稳定性和安全性。

MC34063是一款性能优异、应用广泛的开关电源控制器，适用于各种需要直流-直流变换的场合。通过合理的设计和调试，可以充分发挥其性能优势，为各类电子设备提供稳定可靠的电源供应。