EEPW论坛

在推导包含R g 的双运放仪表放大器的增益时，我们确实需要更加小心，因为电路结构相对复杂。这里，我们将使用节点电压法和叠加原理来详细推导增益表达式。

假设有以下电路元件和标记：R 1  和 R 2  是仪表放大器输入端的两个电阻，通常相等，即 R 1 =R 2 =R。

R g  是输入信号源与仪表放大器输入端之间的电阻。

A 1  和 A 2  是两个运算放大器，通常配置为同相和反相放大器。

V in  是输入信号电压。

V out  是仪表放大器的输出电压。

电路结构通常如下：

V in  通过 Rg  连接到 R 1  和 R 2  的公共节点（我们称之为节点A）。

节点A 分别通过 R 1  和 R 2  连接到两个运算放大器的输入端。

运算放大器的输出端通过反馈电阻（未在图6中明确标出，但通常存在）和可能的其他电阻网络连接到输出端 V out 。

为了简化推导，我们假设两个运算放大器都是理想的（即无限大的开环增益、零输入偏置电流和零输出阻抗），并且反馈电阻网络配置为提供所需的增益。

使用节点电压法和叠加原理来推导增益：

节点电压法：设节点A的电压为 V A 。

根据节点电压法，我们可以写出节点A的电压方程，考虑到 V in  通过 R g  连接到节点A，以及 R 1  和 R 2  的分流作用。

叠加原理：

我们将输入信号 V in  视为一个独立源，并分别考虑它对两个运算放大器输入端的影响。

由于运算放大器是理想的，我们可以假设它们的输入端电压分别等于节点A的电压（对于同相放大器）和某个与 V A  相关的电压（对于反相放大器，这通常涉及到反馈电阻网络）。

增益推导：

找到 V out  与 V in  之间的关系。

这通常涉及到解一组线性方程，这些方程描述了运算放大器的输入-输出关系以及电阻网络的分压作用。

得到一个表达式，描述了仪表放大器的增益 G= V in /V out ，这个表达式将包含 R 1 、R 2 、R g  以及反馈电阻网络的参数。

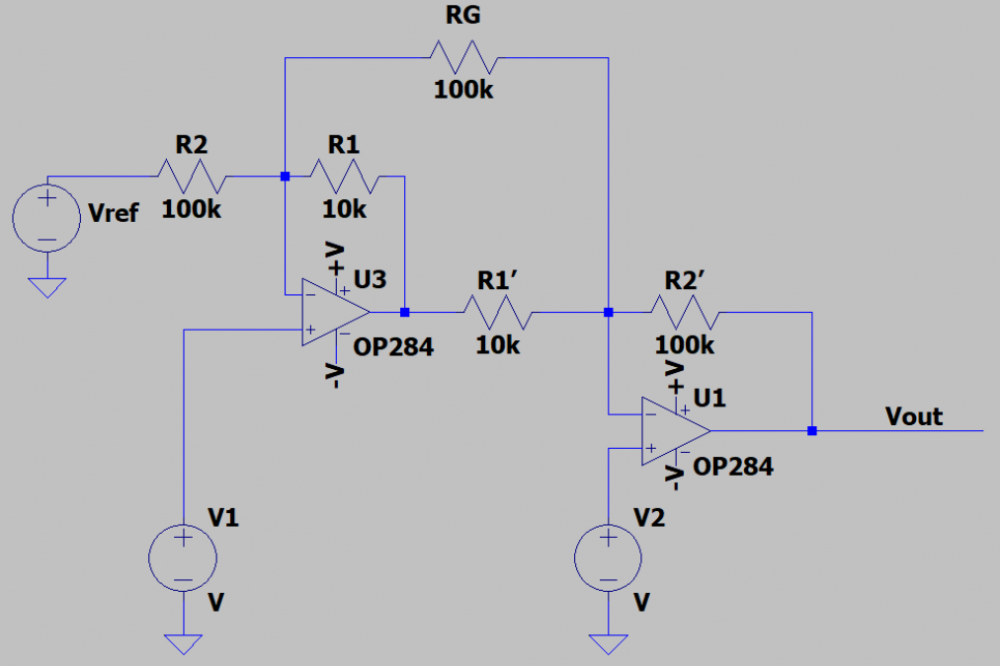
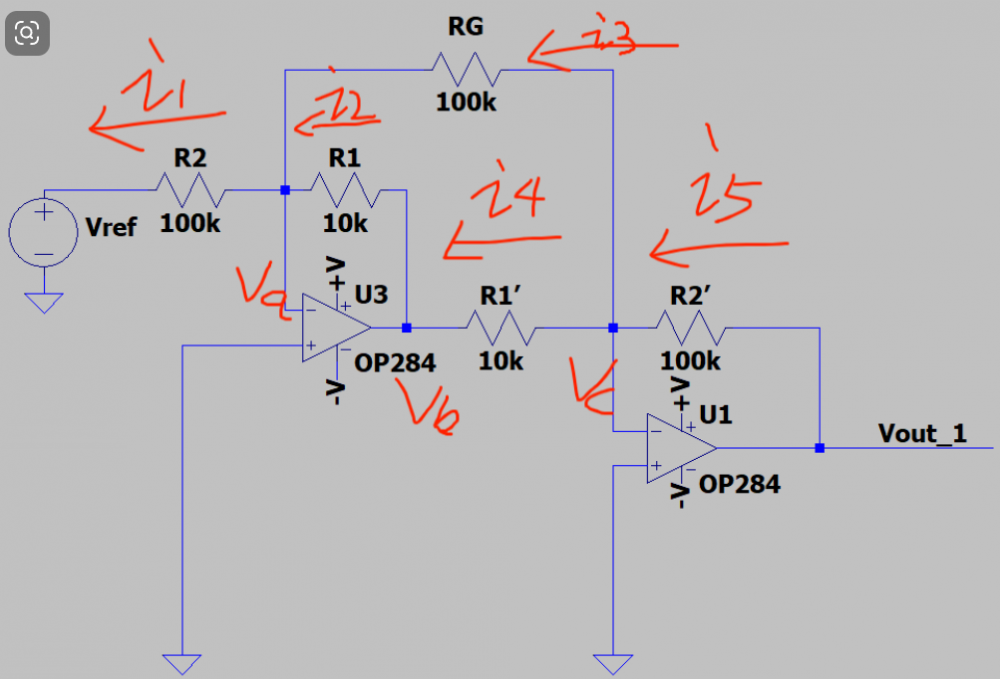
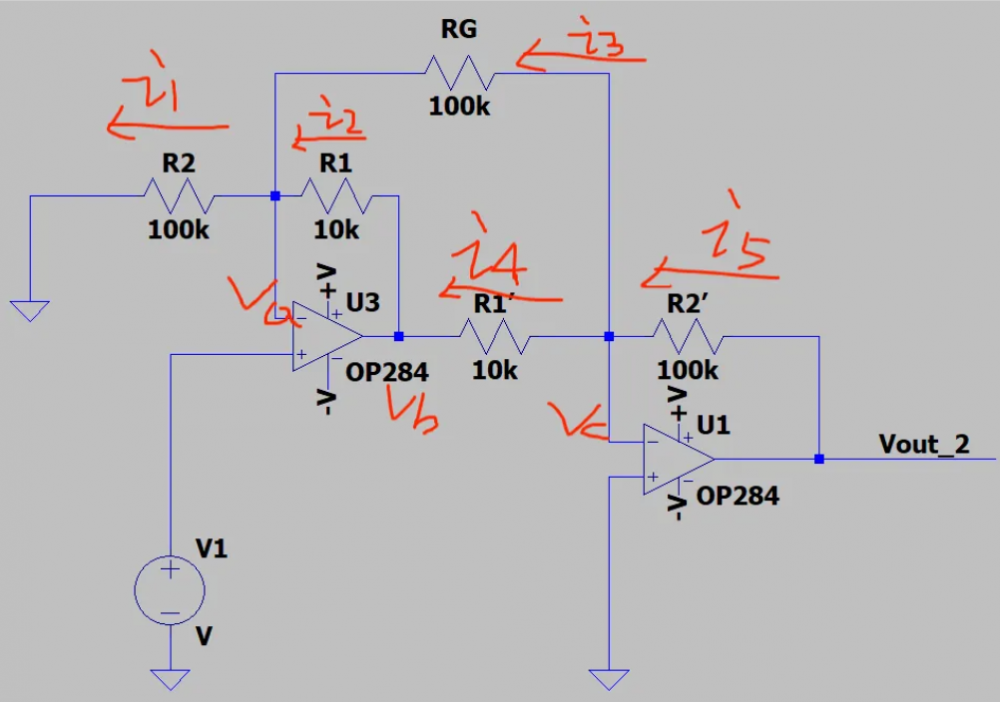
第一级运算放大器（U3）

电路结构：U3 构成一个差分放大电路。同相输入端接输入电压V1，反相输入端通过电阻R1（10kΩ）连接到输出端的反馈信号，同时通过电阻R2（100kΩ）连接到基准电压Vref。输出端还通过电阻RG（100kΩ）反馈到反相输入端，形成深度负反馈。

工作原理：基于运算放大器 “虚短”（同相端和反相端电压近似相等）和 “虚断”（流入同相端和反相端的电流近似为 0）的特性。设同相输入端电压为V+3，反相输入端电压为V+3=V1，则，。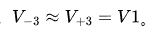

流入反相输入端的电流可根据基尔霍夫电流定律（KCL）分析。通过的电流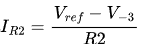，通过R1和RG的电流关系也遵循 KCL。

输出电压的表达式可根据运算放大器的特性和电路中的电阻关系推导得出：

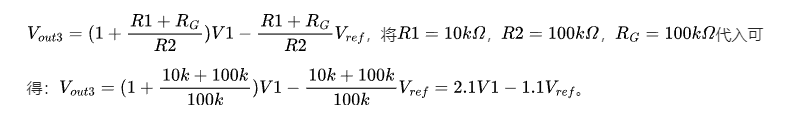
第二级运算放大器（U1）

电路结构：U1 构成一个反向比例放大电路，同时也有差分输入的性质。其反相输入端通过电阻R1`（10kΩ）连接到第一级 U3 的输出电压Vout3，通过电阻R2`（100kΩ）连接到自身输出端Vout；同相输入端接输入电压V2。

工作原理：依据运算放大器 “虚短” 和 “虚断” 特性，设同相输入端电压为V+1，反相输入端电压为V-1，则，。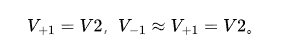

Vref，其他输入源为零:其他输入源为零，只有Vref的电路，我们先根据KCL列出电流方程来。各个节点的电压已经在图中标出来了，那么剩下的步骤就是根据电流方程把电压代入进去。

根据"虚断"列出电流方程

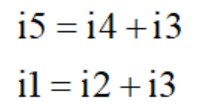
每个电流用电压替换

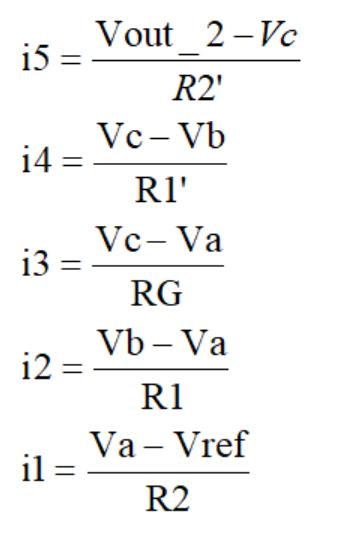
给定条件

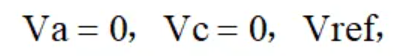
根据等式列出方程

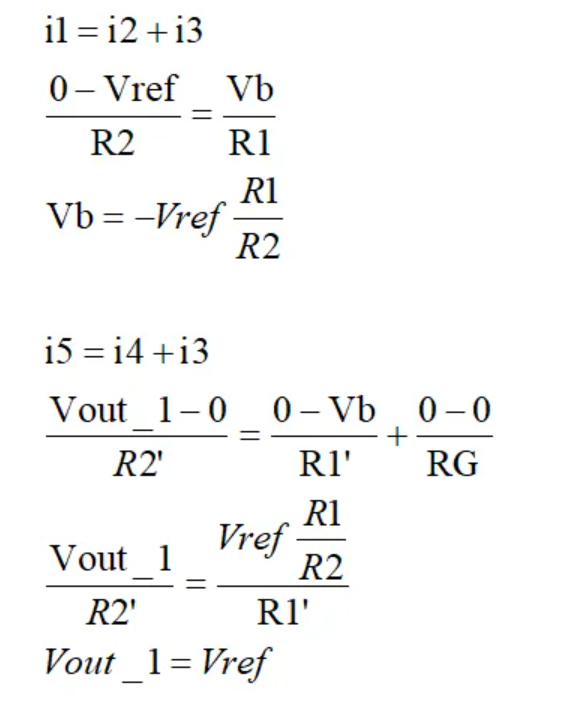
V1，其他输入源为零

根据等式列出方程

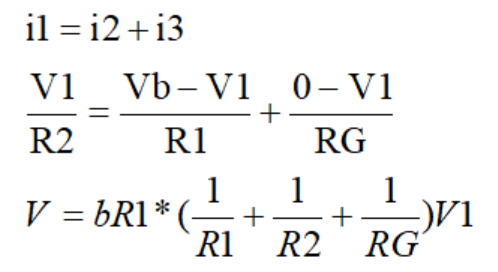
V2,其他输入源为零

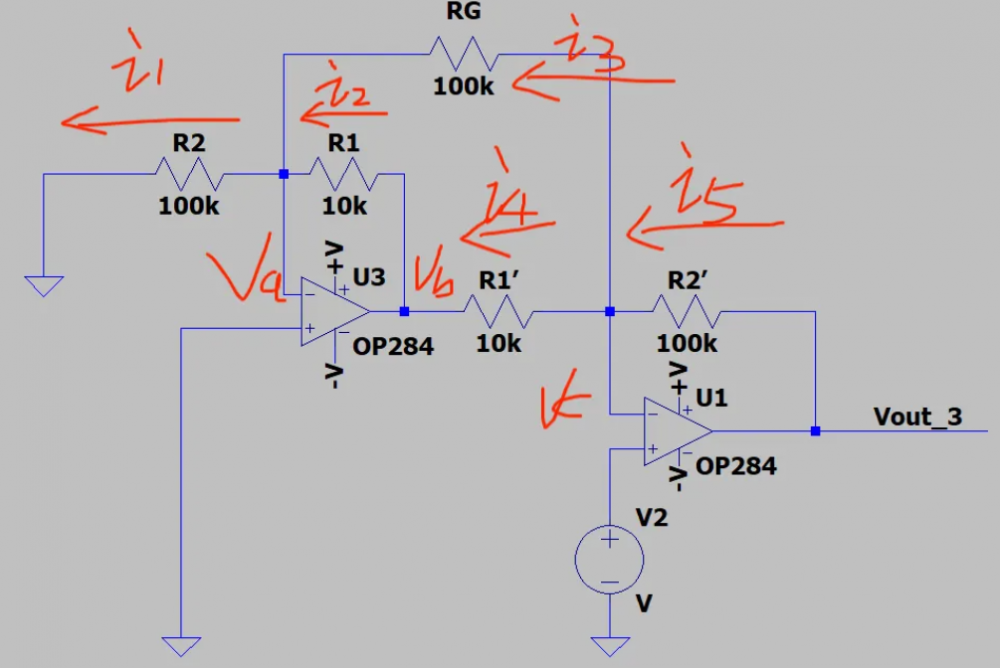
根据"虚断"列出电流方程

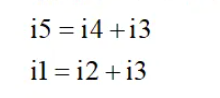
每个电流用电压替换

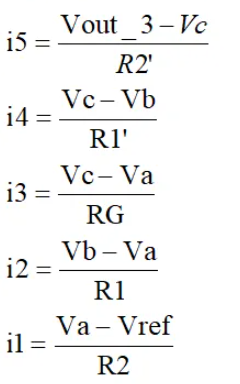
总结：

本文详细推导了包含R g 的双运放仪表放大器的增益表达式。通过节点电压法和叠加原理，考虑了输入信号V in 对两个运算放大器输入端的影响，以及电阻网络的分压作用。接着，以具体的电路结构为例，分析了第一级运算放大器（U3）和第二级运算放大器（U1）的工作原理。在第一级中，U3构成差分放大电路，通过深度负反馈实现电压放大。在第二级中，U1构成反向比例放大电路，同时具有差分输入性质。通过列出电流方程和电压替换，分别推导了在不同输入源下的电压表达式，为计算仪表放大器的总增益提供了基础。整个推导过程展示了运算放大器在复杂电路中的应用，以及如何通过理论分析和数学计算来求解电路参数。