EEPW论坛

RC 滤波电路

RC 滤波电路 是一种由电阻R和电容C组成的简单电路，用于滤除信号中的特定频率成分。根据电路结构的不同，RC 滤波电路可以分为 低通滤波器Low-Pass Filter 和 高通滤波器High-Pass Filter。以下是 RC 滤波电路的基本原理、类型和应用。

RC 滤波电路的基本原理

电阻R和电容C的特性：电阻,阻碍电流流动，产生电压降。电容：存储电荷，对交流信号呈现阻抗容抗，容抗与频率成反比。

滤波原理：利用电阻和电容对不同频率信号的响应差异，实现滤波功能。低频信号可以通过电容，而高频信号会被电容短路或衰减。

RC 滤波电路的类型

RC 低通滤波器（Low-Pass Filter）

功能：允许低频信号通过，衰减高频信号。

工作原理：低频信号：电容的容抗较大，信号主要通过电阻输出。高频信号：电容的容抗较小，信号被电容短路到地，输出信号衰减。

截止频率（f c ）：

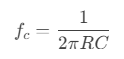
低于 f c  的信号通过，高于 f c  的信号被衰减。

RC 高通滤波器High-Pass Filter

功能：允许高频信号通过，衰减低频信号。

工作原理：高频信号：电容的容抗较小，信号主要通过电容输出。低频信号：电容的容抗较大，信号被电阻衰减。

截止频率（f c ）：

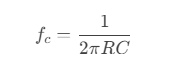
高于 f c  的信号通过，低于 f c  的信号被衰减。RC 滤波电路的特性

频率响应：

低通滤波器：低频通过，高频衰减。高通滤波器：高频通过，低频衰减。

相位变化：低通滤波器：输出信号相位滞后于输入信号。高通滤波器：输出信号相位超前于输入信号。

衰减斜率：RC 滤波器的衰减斜率为 -20 dB/十倍频程，属于一阶滤波器。

RC 滤波电路的应用

信号处理：用于去除信号中的高频噪声或低频干扰。在音频设备中，低通滤波器用于去除高频噪声，高通滤波器用于去除低频杂音。

电源滤波：用于平滑直流电源中的纹波，去除高频噪声。

通信系统：在调制解调器中，用于分离不同频率的信号。

传感器信号调理：

用于滤除传感器输出信号中的噪声，提高信号质量。

RC 滤波电路的设计要点

截止频率的选择：根据应用需求选择合适的截止频率 f c ，通过调整 R 和 C 的值实现。

电阻和电容的选择：电阻值不宜过大，否则会降低信号幅度。电容值不宜过大，否则会增大电路体积和成本。

负载效应：负载电阻会影响滤波器的性能，设计时需考虑负载的影响。

多阶RC低通滤波是一种比较常用的方法，如下图的二阶RC滤波电路：

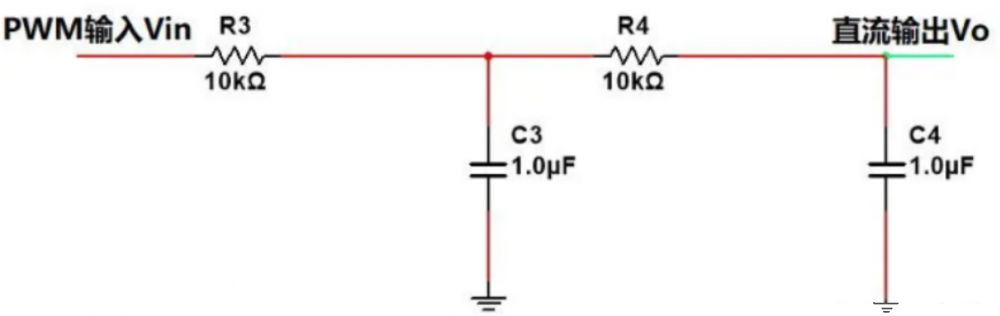
拉普拉斯变换

单位阶跃信号定义为：

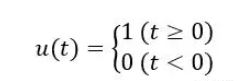
其拉普拉斯变换定义为：

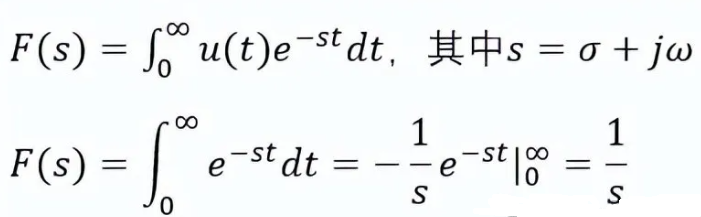
如果PWM信号的高电平为VH，当输出高电平时，输出信号的拉普拉斯变换为：

电容C3，C4在频域下的阻抗分别为以及,得到频域下的等效电路和参数：

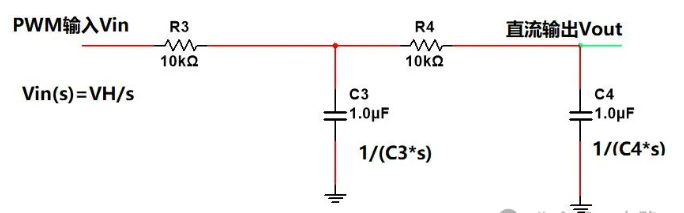
在Octave中使用符号运算来处理复杂的电路分析和信号处理任务是一个很好的选择。尤其是当涉及到分式多项式的运算时，符号运算能够大大减少出错的可能性。

在Octave中如何使用符号运算包来计算电容C4两端电压的示例脚本。假设你已经根据频域下的电路得到了相关的传递函数。

确保你已经安装了Octave的symbolic包。如果还没有安装，可以在Octave命令行窗口运行以下命令来安装：

pkg install -forge symbolic

安装完成后，每次使用前需要加载该包：

pkg load symbolic

接下来是一个示例脚本，用于计算电容C4两端的电压。假设你已经有了相关的传递函数或电路方程，这里我们将模拟一个简单的例子来说明如何使用符号运算：

% 加载符号运算包
pkg load symbolic

% 定义符号变量
syms s C1 C2 C3 C4 R1 R2 V_in(s) % V_in(s) 是输入信号的拉普拉斯变换

% 假设电路参数（这里使用示例值，实际使用时替换为实际值）
C1 = 1e-6; % 1微法
C2 = 2e-6; % 2微法
C3 = 1e-6; % 1微法
C4 = 3e-6; % 3微法
R1 = 1e3;  % 1千欧
R2 = 2e3;  % 2千欧

% 假设输入信号 V_in(s) = 1/s （直流源）
V_in = 1/s;

% 根据电路分析，写出C4两端电压 V_C4(s) 的表达式
% 这里仅作为示例，你需要根据实际的电路分析来写出这个表达式
% 假设电路是一个简单的RC网络，且我们已经知道V_out(s)与V_in(s)的关系
% 例如: V_out(s) = (R2*C3*s + 1) / ((R1 + R2)*C3*C4*s^2 + (R2*C3 + R1*C4)*s + 1) * V_in(s)
% 其中V_out(s)是C4两端的电压
V_out = (R2*C3*s + 1) / ((R1 + R2)*C3*C4*s^2 + (R2*C3 + R1*C4)*s + 1) * V_in;

% 简化表达式
V_C4 = simplify(V_out);

% 显示结果
disp('V_C4(s) = ');
pretty(V_C4);

Octave符号运算

当输入信号时，根据频域下的电路，可以计算出电容C4两端的电压。

涉及到分式多项式的运算，运算量大，容易算错。

可以使用Octave的符号运算快速得到结果。

Symbolic符号运算包需要用到Python的SymPy库。

在Octave的命令行窗口，运行pkg install -forge symbolic，下载symbolic符号运算包，

再运行pkg load symbolic，加载symbolic符号运算包。

运行以下脚本：

syms R3 R4 C3 C4 s VH
ZC4=1/(C4*s);%电容C4的阻抗
ZC3=1/(C3*s);%电容C3的阻抗
Z1=R4+ZC4;%Z1为R4与C4串联
Z2=ZC3*Z1/(ZC3+Z1);%Z2为C3与Z1并联
Vo=VH/s*Z2/(Z2+R3)*ZC4/Z1;%C4两端的电压为Z2与R3分压之后，再由C4与R4分压
simplify(Vo)%化简符号表达式

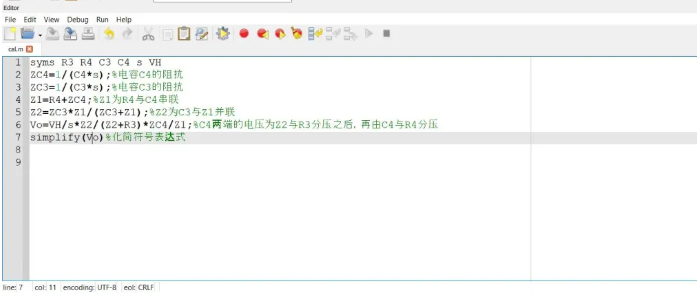
得到电容C4两端电压Vo(s)为:

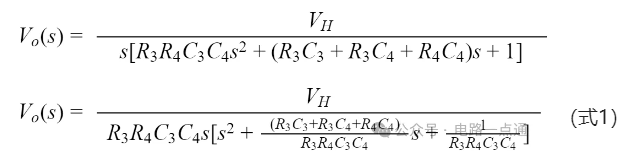
拉普拉斯逆变换

得到，C4两端的电压在时域的表达式为：

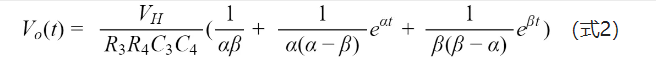
PWM输出直流的纹波分析

当R3=R4=10kΩ，C3=C4=1uF时，a,b分别是以下方程的两个根，

的两个根，

根据求根公式，得到,

的两个根，

假设，

当PWM的频率为800Hz时，占空比为100%时，充电的最长时间为1.25ms，

此时，at最大为-38.2*1.25ms=-0.04775<1，

而bt最大为-261.8*1.25ms=-0.32725<1，

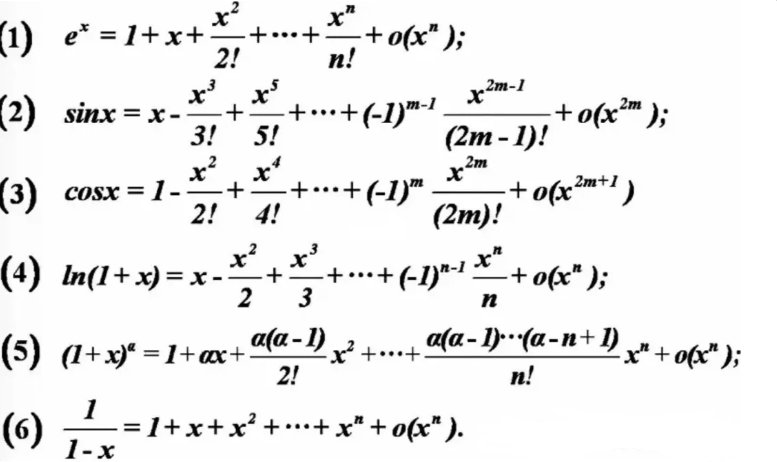
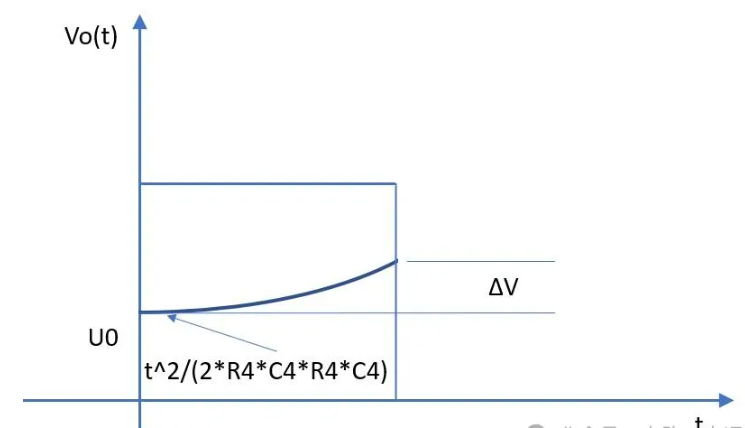
RC滤波电路的基本原理、类型、特性、应用以及设计要点，并且提到了使用Octave的符号运算包来计算电容C4两端电压的示例。此外，还涉及了PWM输出直流的纹波分析。以下是对您内容的总结和补充：

RC滤波电路总结

基本原理：

电阻R阻碍电流流动，产生电压降。

电容C存储电荷，对交流信号呈现阻抗（容抗），容抗与频率成反比。

利用R和C对不同频率信号的响应差异实现滤波功能。

类型：

低通滤波器：允许低频信号通过，衰减高频信号。

高通滤波器：允许高频信号通过，衰减低频信号。

特性：

频率响应：低通滤波器低频通过，高频衰减；高通滤波器高频通过，低频衰减。

相位变化：低通滤波器输出信号相位滞后；高通滤波器输出信号相位超前。

衰减斜率：-20 dB/十倍频程，属于一阶滤波器。

应用：

信号处理：去除高频噪声或低频干扰。

电源滤波：平滑直流电源中的纹波。

通信系统：分离不同频率的信号。

传感器信号调理：滤除噪声，提高信号质量。

设计要点：

截止频率的选择：根据应用需求选择合适的f_c。

电阻和电容的选择：电阻值不宜过大，电容值不宜过大。

负载效应：设计时需考虑负载对滤波器性能的影响。

Octave符号运算示例

在Octave中使用符号运算包来计算电容C4两端电压的示例脚本已经给出，这里不再重复。需要注意的是，脚本中的电路参数和传递函数表达式应根据实际的电路分析来确定。

PWM输出直流的纹波分析

纹波产生原因：

PWM信号在转换为直流信号时，由于开关动作和滤波电路的不完美性，会产生纹波。

分析方法：

通过拉普拉斯变换和符号运算，可以计算出电容C4两端的电压在频域和时域的表达式。

根据电路参数和PWM信号的频率、占空比，可以分析纹波的大小和频率。

减小纹波的方法：

增加滤波电容的容量。

选择合适的电阻值。

提高PWM信号的频率。

优化滤波电路的设计。

示例分析：

当R3=R4=10kΩ，C3=C4=1uF时，可以通过求解方程得到纹波的根。

根据PWM的频率和占空比，可以计算出充电的最长时间和纹波的最大值。

通过比较纹波最大值和1的关系，可以判断纹波是否在可接受的范围内。

总结

RC滤波电路在信号处理、电源滤波、通信系统和传感器信号调理等方面有着广泛的应用。通过合理的电路设计和参数选择，可以实现有效的滤波效果。利用Octave的符号运算包可以方便地计算电路中的电压和电流等参数，为电路设计和分析提供了有力的工具。在PWM输出直流的纹波分析中，通过合理的分析和计算，可以减小纹波对电路性能的影响，提高电路的稳定性和可靠性。