EEPW论坛

　有源滤波器是测试测量电路中经常会使用到的电路，大家也经常会看到诸哪MFB滤波器，巴特沃斯滤波器，等各种不同的说法，下面带大家一起来认识有源滤波器。

　　一.滤波器的频率响应

　　滤波器可分为低通滤波器、高通滤波器、带通滤波器、带阻滤波器等四种，由于四种滤波器可相互转化，本文为行文方便全部以低通滤波器为例进行说明。

　　理想的低通滤波器幅频特性曲线如下图所示，即通带增益恒定，过渡带无穷小，过渡区域斜率无穷大，阻带增益为0。但这样理想的幅频特性在现实当中是不存在的。因此滤波器设计的中心问题，就是要计算出一个响应曲线，按照规定的精确度逼近理想情况的滤波器，并在实验室中制作实现。下图实线即为这样一条低通滤波器的实际响应曲线。

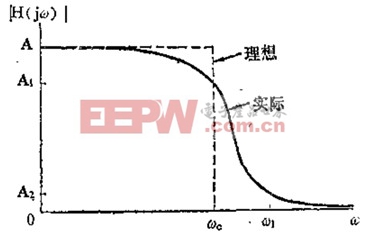
　　实际电路设计普遍被大家接受的滤波器幅频响应特性包括以下几种：巴特沃斯滤波器，切比雪夫滤波器，椭圆滤波器，贝塞尔滤波器等多种。

　　1.巴特沃斯滤波器

　　具有最大幅度平坦度特性，使用该滤波器可获得尽可能平坦的通带幅频响应。高于截止频率的频带衰减具有适中的斜率，其脉冲响应具有适当的过冲及振铃。下图为不同阶数巴特沃斯滤波器的幅频响应和时域响应。

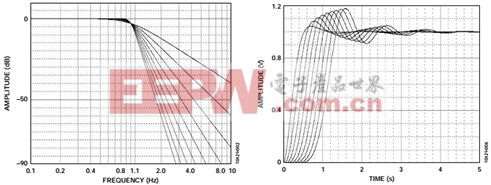
　　2.切比雪夫滤波器

　　与巴特沃斯型相比，此类滤波器在通带以外的衰减更为陡峭，但这是以牺牲通带内的纹波为代价的。切比雪夫滤切比雪夫滤波器的截止频率定义为响应滚 降至低于纹波带的频点。对于偶数阶滤波器而言，所有纹波均高于0 dB了益的直流响应，因此截止频点位于0 dB 衰减处。对于奇数阶滤波器来说，所有的纹波均低于0 dB了益的直流响应，截止频率则定义为低于纹波带最大衰减点(- ripple dB的频点)。在极点数量一定时，增加通带纹波可实现更陡峭截止。相对于巴特沃兹滤波器而言，切比雪夫滤波器的脉冲响应具有更大的振铃。

　　下图为此型滤波器的频域与时域响应。

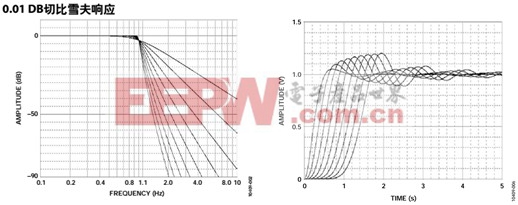
　　3.贝赛尔

　　也称为汤姆逊(Thomson)型滤波器。由于其线性相位响应特性，使得此类滤波器具有最优的脉冲响应(最小化过冲及振铃)性能。对于给定的极点数量而言，贝赛尔的幅频响应并不如巴特沃兹平坦，-3 dB 截止频率以外频带的衰减也不如巴特沃兹陡峭。尽管须采用更高阶的贝赛尔滤波器来逼近给定的巴特沃兹滤波器的幅频响应，但考虑到贝赛尔滤波器的脉冲响应保真度，增加一定的复杂性(源于附加的滤波器部件)也是物有所值的。

　　下图此型滤波器频域响应与时域响应。

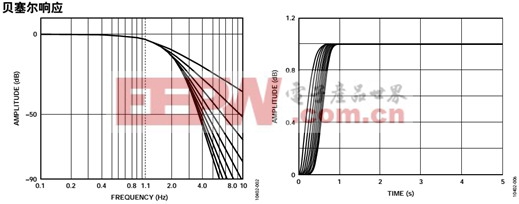
　二. 滤波器电路拓扑结构

　　对于有源RC滤波器来说，单运放一般最高只能设计二阶滤波器，更高阶的滤波器由多个一阶或二阶滤波器串联而成。下面以二阶有源滤波器为例介绍常见滤波器拓扑结构。

　　1.MFB

　　也称为无限增益拓扑(或Rauch拓扑)，对元件值改变的敏感度较低，因此较为常用，其典型电路拓扑如下图所示。

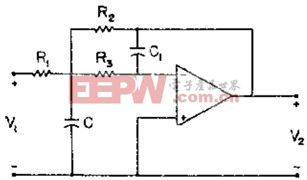
　　2.Sallen Key

　　在某些例子中，Sallen-Key拓扑证明更为优秀。就经验法则而言，下列情况时，Sallen-Key拓扑更佳：

　　1)增益精度较为重要，
　　2)采用了单位增益滤波器，以及
　　3)极点对Q值较低(例如，Q <3)

　　在单位增益时，由于运算放大器被用作单位增益缓冲器，使得 Sallen-Key拓扑具有了与生俱来的卓越增益精度。对MFB拓扑而言，增益则取决于R2/R1的电阻比值。单位增益Sallen-key拓扑还具有 元件需求较少的优势(仅需两个电阻，MFB需三个电阻)。在应用于高Q值高频率滤波器部件之时，Sallen-Key拓扑也是可取的。在此类部件中，若采 用MFB设计，C1值必需很低以得到合理的电阻值。下图为Sallen Key低通波器的典型电路图。

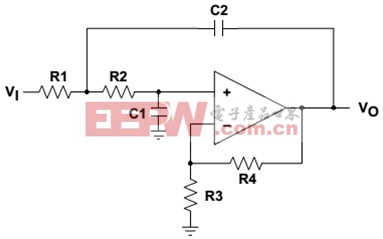
　　3.双二次型

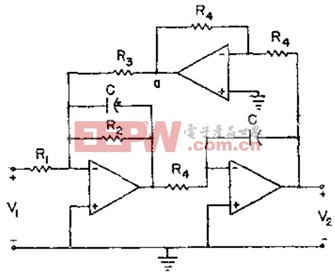
　　双二次型与前面两种电路相比，需要使用更多的元件，但便于调整并具有很好的稳定性，在设计高阶滤波器进行多级级联时更有优势。

　　三. 滤波器设计

　　由于有源滤波器频率响应特性计算复杂，目前进行滤波器设计时一般采用计算机进行辅助设计。目前应用比较广泛的滤波器设计软件有Filter Solutions，FilterPro等专用软件。值得一提的是，FilterPro为TI公司的免费软件，大家可以直接从TI官方网站免费下载。