EEPW论坛

 无论在何种情况下，两个具有不同电位的导体间都会产生电容。在两个具有不同电位的导体之间，总是存在一个电场。电场中存储的能量由驱动电路供给。因为驱动电路是一个功率有限的激励源，所以在任何两个导体之间的电压将在有限的时间内建立一个稳定状态值。随着能量的注入，电压会很快地建立或衰减，其中对电压的阻力称为电容。例如两个平等金属板的结构，在低电压下包含了大量电荷，所以电容就很大。

        图1.5显示了由30欧激励源驱动一个电容时理想的电流和电压波形，电容阶跃响应的上升变化显示为一个时间的函数。当电压阶跃刚开始时，大量的能量流入电容，从而建立起它的电场。进入电容的初始电流相当高，而电压阶跃刚开始时，大量的能量流入电容，从而建立起它的电场。进入电容的初始电流相当高，而电压与电流的比值Y(T)II(T)非常低。在很短的时间范围内，电容看起来就像一个短路连接。

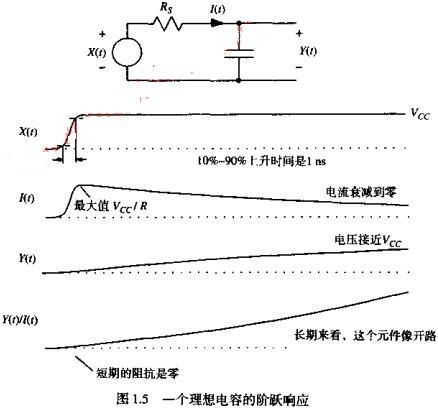
        随着时间的推移，比值Y(T)II(T)逐渐增大。最终，电流下降至接近于零，电容此时看起来像开路一样。最后，电容内的电场完全建立，由于电介质非理想的绝缘性质，电容两极之间只有一个很小的泄漏电流存在。此时的Y(T)II(T)比值非常高。

        有此电路元件的阶跃响应在某个时间范围内显示为电容特征，而在另外的时间范围内显示为电感特征，或者相反，举例来说，电容的安装引脚在非常高的频率时，其电感通常足以使整个元件呈现为电感特征。该电容的阶跃响应在零时刻会出现一个微小的脉冲，也许仅有数百皮秒(对应于引脚电感大小)，接着下降至零，随后才是一个正常的容性上升斜线。

        如果阶跃激励源的上升时间太慢，输出曲线的轨迹将不会出现电感性尖脉冲。由于脉冲非常短，如果示波器的扫描时间基准设定得太慢，也很容易会错过。令人感兴趣的是，通过调整上升时间和设定扫描时间基准，我们可以使电路元件的阶跃响应测量结果在某个特定频率范围内特征更加突出。概括来说，如果阶跃上升时间是TR，接近零时刻的阶跃响应与电路元件在频率FA附近的阻抗大小有关：FA=0.5/TR

        其中，TR=阶跃激励源的上升时间

        FA=近似分析频率

        通过直观地平均整个时间周期上的阶跃应值，我们可以休息出较低频率上的阻抗大小。采用上式可以计算出应于一个平均周期值TR的近似分析频率。

        阶跃响应的最终数值显示出了直流时的阻抗。

        仅从一个阶跃上升时间TR，我们无法推断出比FA更高的频率分量上更多特性。只有阶跃激励源的信号频率足够高，才能确保揭示出所想要看到的情况。

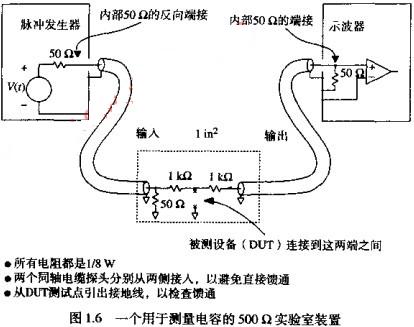
        图1.6描绘了一个测量装置，适合用来表现一个几皮法电容在纳秒级时间周期上的特性。这个装置适用于揭示诸如印刷电路走线、六电路输入电容、旁路电容元件以及其他数字电路通用元件的电容特性。该方法通过一个已知的电阻来驱动被测电容。通过测量产生波形的上升时间，可以推导出电容的容值。与音频电路所用技术相比较，这个装置非常复杂。复杂性来自于在高频电磁场能量的控制和引导方面的困难。同轴电缆用来直接引导测试信号，并把测量结果输入输出到一个小于1IN的完整地平面，该处是实际进行测量的位置。把测量区域限制为NIN，是为了确保电路呈现为集总电路的特性。

例1.1 一个小的接地电容的测量

        本例中(见图1.6)的被测设备(DUT)是一个平行板电容器。采用0.5IN*0.75IN的1.5IZ覆铜印制在环氧树脂FR-4印刷电路板正面，背面是一个平行的完整地平面，标称的平行间隔为0.008IN。这个结构一个电容器，附带有非常低的寄生串联电感。

        测量装置由两个RG-174同轴电缆组成，分别用于信号的输入和输出。输入电缆通过50欧端接到地，已端接的信号输出通过一个1K的驱动电阻连接到被测设备。1K电阻隔离了被测设备与信号源，为信号幅度性能的一致性，面无需考被测设备的负载阻抗。

        实际路中的信号源脉冲发生器应能提供幅度及上升时间与期望相近似的信号。当测量无源元件时，脉冲发生器的直流偏置不太重要。另一方面，当测量门电路输入时，通常应使脉冲源的输出覆盖门电路输入的整个转换范围，并向被测门电路提供能量，以使门电路偏置于实验所需的工作范围之内。需要较大输入驱动电流的门电路可能还会要求比1K更小的源端电阻。

        如果信号发生器具有一个50欧的反端接器件，利用它可以减少输入电缆上的反射。该器件在信号发生器输出级插入一个50欧的串联阻抗，可以减少信号源电缆的前向和反向反射，该反射通常是由测试夹具与信号源输出阻抗之间不可避免的轻微不匹配而引起的。反向端接后，来自源信号的不必要反射被两次衰减，第一次是被测试夹具弹回时，第二次是在源端反向端接电阻上反弹后返回到测量仪器的路径上，反向端接虽然使信号源输出的有效幅度降低了一半，但是改善了系统阶跃响应。

        输出电缆通过一个1K电阻与被测电路隔离连接，另一端连到一个内部含有50欧端接的示波器输入端。1K电阻起一个21：1探头的作用。这里的输入和输出电缆都是3FT长。

        输出电缆通过一个1K电阻与被测电路隔离连接，另一端连到一个内部含有50欧端接的示波器输入端。1K电阻起一个21：1探头的作用。这个信号感应装置的优点将在本书后面关于示波器探索测的小节中详细阐述。这里的输入和输出电电缆都是3FT长。

        当信号源的阶跃输入为2.6V，且DUT断开时，这个探头的开路响应结果如图1.7所示。顶部的扫描线是以5NS/刻度记录的，底部的扫描线记录的是同一信号放大为500PS/刻度的视图。

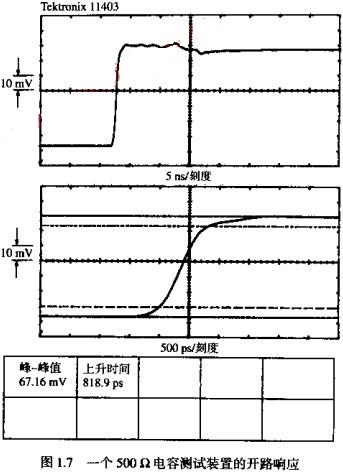
        用于记录这个波形的TEKTRINIX11403示波器自动计算出的10~90%上升时间为818PS标称阶跃幅度的1/21，而DUT上幅度1.3V是信号源驱动电压的一半。

        如图1.8所示，这个实验配置的戴维南等效电路，将总系统上升时间都集中表现到信号源上。这里不关心究竟是信号源还是示波器使得观察到的上升的时间变得更慢。任何一个具有近似开路的时间的信号源与示波器的合理组合，在这个DUT的影响下都会有类似的特性。我们只关心已知的信号源-示波器的合理组合，在这个DUT的影响下都会有类似的特性。我们只关心已知的信号源-示波器组合的总上升时间。当测量无源元件时，我们同样只关心观察到的阶跃幅度，而DUT上实际的电压细节的探头衰减比例都不重要。

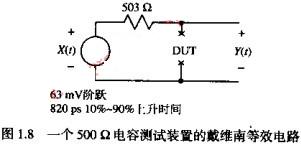
        关掉脉冲源而仍然保持50欧反向端接的连接，采用一个欧姆表在DUT的端子上测量，得到信号源的源端阻抗为503欧。这个503欧电阻是1K驱动电阻和1K感应电阻关联的结果。

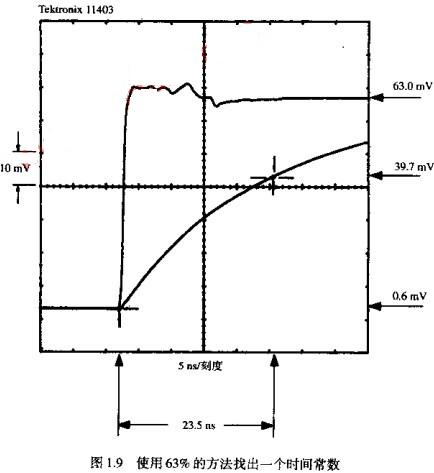
        在连接DUT的情况下，观察到的电压波形显示为电容特性，由低开始然后上升。初始驱动波形的存储副本被重叠在这个图上以便读者参考。通过这个探头，在整个可观察的时间刻度范围上，从800PS(信号源和示波器组合的总上升时间)到40NS(在示波器图中显示的线迹长度)，DUT表现出理想的容性。

        从图1.9中光标沿着上升时间标出的63%的点，我们可以得知RC时间常数时间常数为23.5NS。已知驱动电阻为503欧，我们可以用关系式C=π/R计算出DUT的电容值：

        从这个上升时间的频率之间的关系可以推导出一个粗略的办法，用电容的数字波形前沿来表示电抗。当考虑到由于一个容性负载导致的数字波形失真时，这种方法非学有用。

        XC=T1/XC

        对于一个3NS上升沿。例1.1中的电容的电抗值为20.44欧，由此我们预知它将会使来自输出阻抗为30欧的TTL驱动器的一个3NS上升沿显著畸变。

        在任何时刻，电容上升过的电流与其电压的上升时间的关系总是依照下列通用公式：

        I电容=C DV电容/D1