% $ Date: 10/11/2009 整理: eyes417 $
%##################################################################
%
% FILE : FFT.m
% TITLE: FFT计算仿真,得到频率和幅度值,相位图#此前在首页部分显示#
%
%##################################################################
close all; %先关闭所有图片
Adc = 1.25; %直流分量幅度
A1 = 1; %频率F1信号的幅度
A2 = 0.25; %频率F2信号的幅度
F1 = 100; %信号1频率(Hz)
F2 = 1000; %信号2频率(Hz)
Fs = 5120; %采样频率(Hz)
%P1 = -30; %信号1相位(度)
%P2 = 90; %信号相位(度)
N = 256; %采样点数
t = [0 : 1/Fs : N/Fs]; %采样时刻
%生成信号
%S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %考虑相位
signal1=A1*sin(2*pi*F1*t);
signal2=A2*sin(2*pi*F2*t);
S=A1*sin(2*pi*F1*t)+A2*sin(2*pi*F2*t); %无直流偏置
S=Adc+A1*sin(2*pi*F1*t)+A2*sin(2*pi*F2*t); %直流偏置
%S=Adc+[A1*sin(2*pi*F1*t)+A2*sin(2*pi*F2*t)]/2;
%显示原始信号
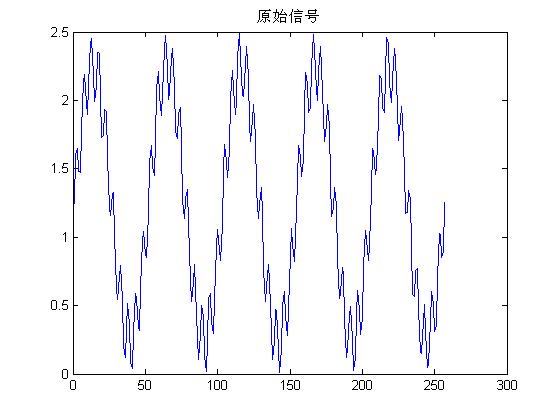
plot(S);
title('原始信号');
figure;
Y = fft(S,N); %做FFT变换
Ayy = (abs(Y)); %取模
plot(Ayy(1:N)); %显示原始的FFT模值结果
title('FFT 模值');
figure;
Ayy = Ayy / (N / 2); %换算成实际的幅度
Ayy(1) = Ayy(1) / 2;
F = ([1:N] - 1) * Fs / N; %换算成实际的频率值
plot(F(1:N/2), Ayy(1:N/2)); %显示换算后的FFT模值结果
title('幅度-频率曲线图');
figure;
Pyy = [1 : N/2];
for i = 1 : N/2
Pyy(i) = phase(Y(i)); %计算相位
Pyy(i) = Pyy(i) * 180 / pi; %换算为角度
end;
plot(F(1 : N/2), Pyy(1 : N/2)); %显示相位图
title('相位-频率曲线图');
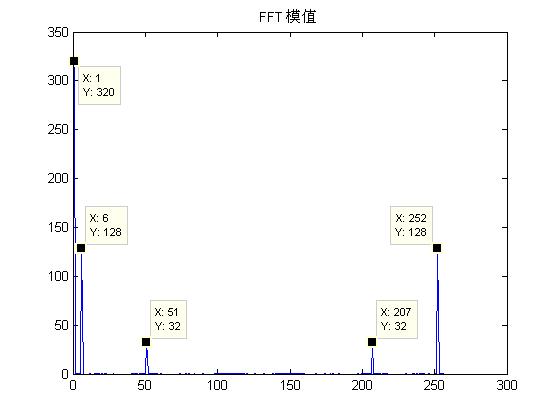
根据公式验证 --- 某点n所表示的频率为: Fn=(n-1)*Fs/N
f1=(6-1)*5120/256=100 (Hz) ---- 验证结果正确
f2=(51-1)*5120/256=1000(Hz)---- 验证结果正确
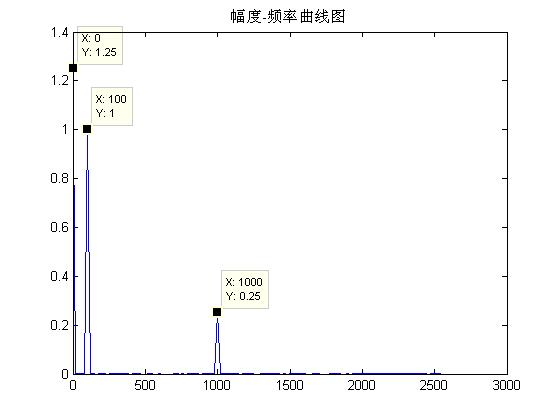
根据公式验证 --- 对于n=1点的信号,是直流分量,幅度即为A1/N --- A1=320/256=1.25 --- 验证结果正确
对于n点(n≠1,且n<=N/2) 幅度A --- A=An/(N/2)=128/(256/2)=1 --- 验证结果正确
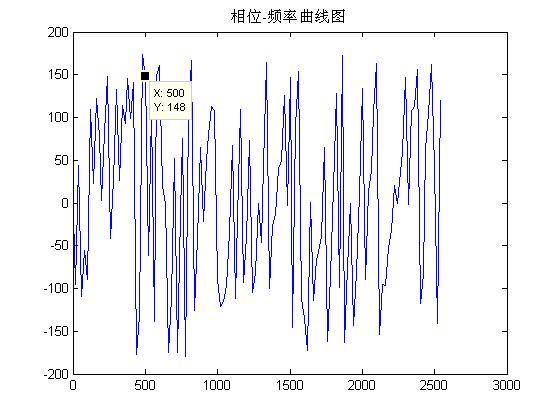
相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。
atan2(500, 148)=x,结果是弧度,换算为角度就是180*(-x)/pi=相位值。
根据FFT结果以及上面的分析计算,--- 频率,幅度.相位....我们就可以写出信号的表达式了,它就是我们开始提供的信号。------ 信号重建

 我要赚赏金
我要赚赏金

