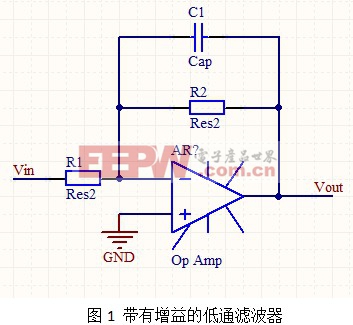
结合波特图和传递函数,不难看出,当系统的频率低于ω1时,电容c1容抗比R2的阻抗值大的多,系统可以近似看为反相放大器,表现出来的为直流的增益,电容的作用可以看做为滤波作用。当系统工作在较高的频率上,电容c1容抗比R2的阻抗值小的多,系统可以近似看为积分电路,其在波特图上的表现为一条-20dB/十倍频的一条直线,与角频率ω的交点为
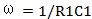
,由于该电路在特定的频率范围内可以近似为一积分电路,此时的电路为一有损耗的积分电路。因此,分析该类型的电路是,首先需知道通过该系统信号的频率范围和系统的极点处,从而达到确定系统的作用。
本文引用地址:http://www.eepw.com.cn/article/185313.htm
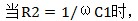
传递函数|H|=|H直流|-3dB,此时的频率为电子电路中常见的-3dB频率点。
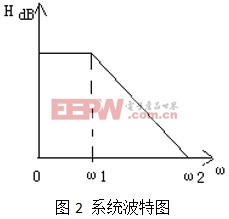
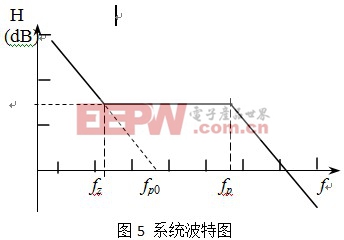
再次仔细分析该系统的波特图,还可以清除的看出
ω<ω0 :信号无衰减通过;
ω>ω0 :信号逐渐衰减或者截断,衰减频率为-20dB/十倍频;
由此,该系统还具有一定程度的低通滤波作用,虽然滤波的性能不是太令人满意。
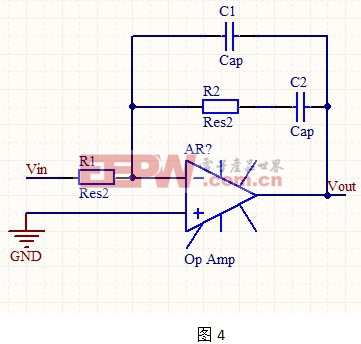
另一种RC反馈的接法为正反馈,如图3:

该电路为模拟电子教课书上经典的RC振荡电路:振荡信号由同相端输入,故构成同相放大器,输出电压Uo与输入电压Ui同相,其闭环电压放大倍数等于Au=Uo/Ui=1+(R4/R3)。而RC串并联选频网络在ω=ωo=1/RC时,Fu=1/3,εf=0°,所以,只要|Au|=1+(R4/R3)>3,即R4>2R3,振荡电路就能满足自激振荡的振幅和相位起振条件,产生自激振荡,振荡频率fo等于fo=1/2πRC,采用双联可调电位器或双联可调电容器即可方便地调节振荡频率。在常用的RC振荡电路中,一般采用切换高稳定度的电容来进行频段的转换(频率粗调),再采用双联可变电位器进行频率的细调。


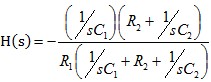
 我要赚赏金
我要赚赏金

