概述
机器人运动系统式一套高复杂性、高耦合性、驱动力小于机体物理自由度的非线性系统,为了实现机器人在空间中稳定的运动姿态控制,本设计把机器人运动系统在空间中的运动形式等效成了旋转倒立摆模型,基于该模型的运动特点,分别设计了速度闭环控制算法和角度闭环控制算法,通过双闭环控制算法来实现对空间中旋转倒立摆的稳定控制。
开发环境
硬件:该设计硬件依托于ART-PI开发平台,主控芯片采用STM32H750高性能单片机,同时采用TB6612芯片作为旋转倒立摆的核心动力驱动,采用霍尔传感器作为速度采集,采用高精度电位器作为摆臂角度采集传感器,采用OLED屏幕来进行参数的显示,与实时调整。
RT-Thread版本:RT-Thread版本采用4.0.2
开发工具及版本:mdk5.32版本
RT-Thread使用情况概述
本设计采用rt-thread4.0.2master版本,用到了该操作系统的全内核、FinSH控制台交互,SPI驱动、ADC驱动、编码器驱动、PWM驱动等相关系统驱动,并且编写了双闭环PID控制算法。
软件框架说明
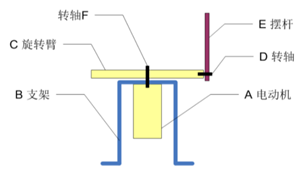
本设计硬件平台基于ART-PI,核心部分已经固定,针对旋转倒立摆机械部分,其结构如下图所示:
软件模块说明
本设计最关键的部分是PID算法的实现,针对倒立摆的运动特点,进行了优化与调整,PID算法的实现基于经典控制理论中线性控制的理论基础:
在工程实际中,应用最为广泛的调节器控制规律为比例、积分、微分控制,简称PID控制,又称PID调节[6]。PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统。为了消除稳态误差,在控制器中必须引入“积分项”。积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此,比例加积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件(环节)或有滞后组件,具有抑制误差的作用,其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。
这就是说,在控制器中仅引入“比例”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象,比例微分(PD)控制器能改善系统在调节过程中的动态特性。
演示效果

比赛感悟
本次比赛基本是利用业余时间一点一点完成,中间遇到了一些困难,主要问题出现在对芯片的底层配置上,不过通过对比手册介绍与仿真,都能初步解决。得益于RT-Thread操作系统完善的内核管理,调试交互,驱动设计、使得在设计中少走了很多弯路,加快了开发速度,推荐大家都来尝试使用该系统,真的很好。

 我要赚赏金
我要赚赏金

