EEPW论坛

作者：Gabe Ayala

欢迎继续关注《定时决定一切》系列文章！上次我们探讨了对 PLL 环路滤波器响应的理解。今天，我将帮助您了解如何更好地理解各种抖动技术规范。
随着高速应用中的定时要求日趋严格，对各种抖动技术规范的更深入理解现已变得非常重要。从 10Gb 以太网网络到 PCIe 等高速互联技术，链路中所暗含的稳健性都与降低定时裕度密切相关。

简言之，抖动就是信号边沿与理想值或理想间隔的偏差。使用一个周期信号作为理想参考值，可在下图中更准确地描述系统中带噪音成分的真实信号，其中噪声源包括电源、热噪声以及交叉耦合干扰等。图 1 是“理想”信号和信号频域表示法。

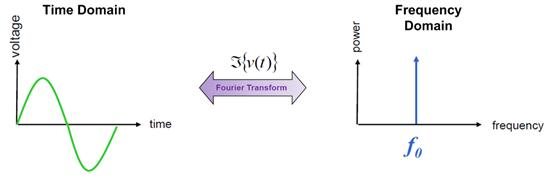
图 1：“理想”信号

由于噪声和扰动对信号有影响，因此得到的波形会受到抖动影响，如图 2 所示。整个频谱上的信号能量传播被称为相位噪声。

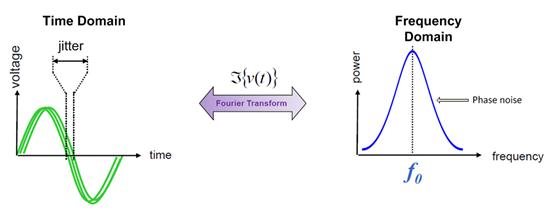
图 2：抖动的影响

抖动可进一步划分为多个子类和技术规范，每一个都有自身的属性和测量方式。主要测量方法包括：周期抖动、循环周期抖动以及相位抖动。虽然这些并未涵盖所有测量形式，但在本文中我们只详细介绍这几种。

周期抖动

周期抖动是指周期时间与上述理想信号周期的偏差。我们随机选择很多个周期，然后计算平均时钟周期（其应该接近理想周期）以及标准偏差与峰至峰值。标准偏差被称为“RMS 抖动”，峰至峰值被称为“Pk-Pk 周期抖动”。

由于周期抖动的随机高斯分布特性，其能量信息完全可由平均偏差和标准偏差来描述。不过，更有用的测量可通过 Pk-Pk 周期抖动产生。知道 Pk-Pk 周期抖动，对于恰当配置系统设置和保持时间来说很有用。下面的等式近似于这种最差情况：

Pk-Pk 周期抖动 = 2σ x（RMS 周期抖动）

恰当的 σ 值源自高斯分布概率密度函数，如表 1 所示。本表可按以下方法读取：对于给定样片量的 N 个周期，有 N-1 个样本周期具有处于该分布平均值的 σN 以内的周期。N 个周期中随后只有 1 个周期超过了该范围。比特误码率可直接使用，即 BER = 1/N。

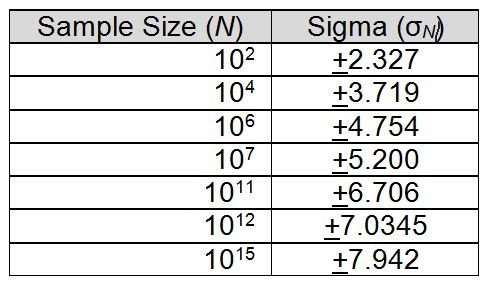
表 1：高斯分布概率

循环周期抖动

循环周期抖动是周期信号中两个相邻周期的周期时间变化。在整个信号数据流中随机选出相邻周期，直到选出足够的样片数量为止 — 通常是 1,000 个以上。相邻周期集中的峰值偏差可按循环周期抖动报告，在扩频计时中特别有用，因为此时周期抖动很容易受到刻意扩频的影响。

相位抖动与相位噪声

在查看目标信号的频域表示时，特定偏移频率（相对于载波）下的噪声值被称为相位噪声，例如 12 MHz 偏移下的 -110dBc/Hz 或 50kHz 偏移下的 -70dBc/Hz。

以下公式是选取目标频段内的分散相位噪声点并对信号相位抖动中的结果进行积分的情况。其中，f0 是载波，f1 和 f2 是载波一侧的积分带宽限值（假设信号是对称的）。

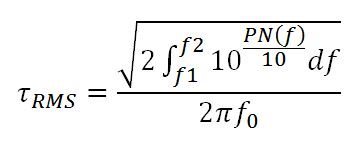
该测量的重要性与周期抖动相似，不过这里周期的分布由其各自的频率生成，因此图 1 和图 2 中的能量扩展幅度更宽。对于通信系统以及 ADC 和 DAC 而言，接收器和发送器共同创建一个带通滤波器，用以创建可接受的噪声品质因数。

时间间隔误差 (TIE)

时间间隔误差是指测量信号相对于“理想”信号的时间偏差。图 3 给出了 TIE 的测量方法。其中，“理想”信号周期通常由测量装置从目标信号的平均周期中生成。TIE 的计算公式如下：

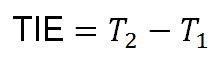
在使用时钟／数据恢复 (CDR) 电路从数据流中恢复参考时钟的应用中，TIE 测量非常有用。如果 TIE 值比较大，则表明恢复的时钟 PLL 无法跟上信号数据速率的变化。

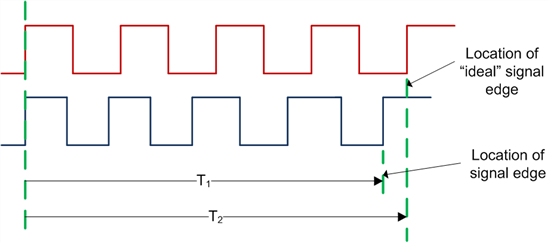
图 3：时间间隔误差测量

感谢阅读《定时决定一切》！希望您现在对抖动技术规范有了更好的理解。

原文请参见: 

http://e2e.ti.com/blogs_/b/analogwire/archive/2014/08/29/timing-is-everything-jitter-specifications.aspx