信号的“无限持续时间”是能够应用傅里叶分析这一强大方法的必要工作假设。在本文中,我们将证明不仅可以将无限能量信号纳入分析,还可以将周期信号纳入分析。
信号的总能量设x(t)为设备的输出信号(图1)。
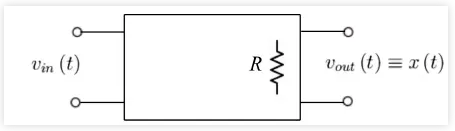
图1:输出信号x(t),其中R表示负载电阻
由于焦耳效应,R消耗的瞬时功率为:

由于W(t)是能量对时间的导数,因此我们可以得到在区间[0,t]内耗散的能量如下:
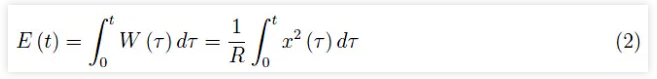
我们隐含地假设是t=0作为初始时刻。然而,这种选择破坏了使用傅里叶变换进行E(t)谱分析的可能性。我们可以按以下方法计算耗散的能量:

假设信号无限地“开启”,则x(t)的总能量由下式给出:

其中,我们设置R=1Ω来归纳定义。
有限能量还是无限能量?注意,在方程(4)中,无论x(t)为多少,都满足以下条件:E≤+∞。也就是说,即使x(t)不可积分,函数x(t)2在区间(−∞,+∞)中仍然可积分,从这个意义上说,积分扩展到(−∞,+∞)可能会产生不定形式∞−∞。有些函数无法在区间(−∞,+∞)内积分,但仍具有柯西主值:
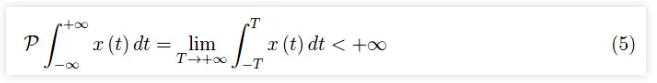
对于这种类型的积分,我们通常有:
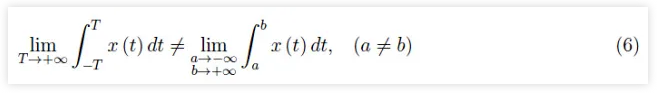
换句话说,积分的值取决于我们如何使积分区间发散。对于这些积分(称为瑕积分),对称区间[−T,T]被视为默认值,并且T趋于无穷大。
此外,函数x(t)2的积分永远不会产生不定形式∞−∞,因为它有一个常数符号,所以我们有E≤+∞。因此,在这个量的情况下,方程(6)可以写成如下:
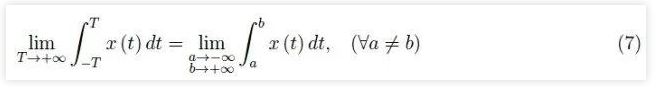
也就是说,x(t)2的积分并不取决于我们如何使积分区间发散。这是一个基本层面,因为如果不是这样,信号的总能量就会随着我们扩大积分区间而改变。
对可求和性以及可积分性的要求似乎是合理的,因为总能量除了唯一确定之外,还必须是一个有限量:E<+∞。在第一步中,似乎有必要参考在无穷远处迅速归零的x(t)信号,以使积分收敛。有些信号虽然不会无限归零,但能量却是有限的。例如,让我们考虑以下信号,为了数学上的方便,其中各种量都用无量纲单位表示:

我们可以直观地理解这一信号的行为:如果指数参数中没有sin2t,我们将得到一个非常正常的高斯信号(正态分布)。然而,参数是由sin2t调制的,这会导致一个非常“窄”的峰值。
反过来,高斯信号的幅度也受到t2的调制。图2中的图形突出显示了这些影响的结果,从中我们可以看到信号不会无限归零,它会被缩小为一系列幅度不断增加(如t2)但宽度不断减小的脉冲。因此,在极限|t|→+∞,单个峰无限高且无限细。所以,它们的面积返回0·∞,可以是一个有限量。这样就有了总的有限面积,积分具有了有限值。
请注意,这些结论看似草率,但实际已经得到了严格的数学分析论证,主要是为了简洁,我们在此省略了分析过程。
在无穷远处具有这种"有限性"必须付出的代价是,函数x(t)在|t|→+∞时没有极限。无论我们把t设得多大,它都取0和t之间的所有值。
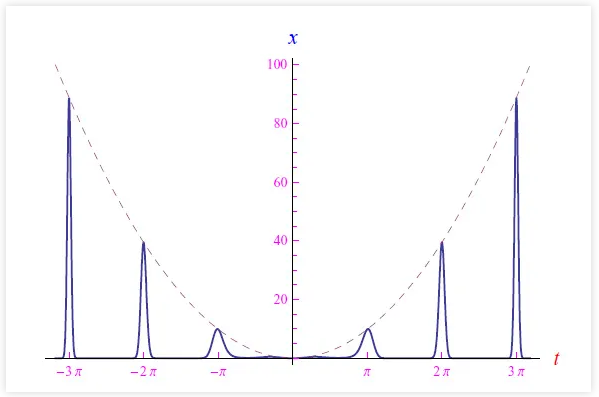
图2:方程(8)的趋势
能谱具有有限总能量的信号x(t)就构成了数学家所说的函数空间L2(−∞,+∞)。它是一个向量空间,其“向量”是可求和的平方函数x(t)。L2上的傅里叶分析由此展开。准确地说,我们可以对任何具有有限能量的信号x(t)进行傅里叶变换:

根据众所周知的帕塞瓦尔定理(Parseval,能量守恒定理),我们有:

其中|X(f)|2是能量谱密度或能谱,即每单位频率间隔内的能量。通常,它被称为功率谱。
恒定信号x(t)=x0=常数,这一类型的恒定信号显然具有无限的总能量。或者,我们可以通过著名的rect()函数截断x(t),该函数在[−T/2,T/2]中是常数x0(其中T>0是信号的持续时间),在该区间外为零。数学家称之为紧支撑函数的函数在物理上非常有趣,它可以使极端的不连续趋势变得“更柔和”,因为它们不会瞬时归零(每个物理过程都有其“关闭”的时间大小,只有在宏观尺度上才可能是瞬时的)。
众所周知,rect()的傅里叶变换是sinc()函数,其以频率为自变量,以持续时间T为自由参数。对于后者的给定值,我们发现f=0是主要频率,因为sinc函数在该值附近峰值达到极大值,而其他频率则由无限抵消的尾部振荡决定。
然而,随着信号持续时间T的增加,同步峰值会逐渐变得更加明显,同时尾峰也会减少。这有一个直接的物理解释:随着T的增加,信号趋于恒定,因此非零频率的贡献将逐渐变得微不足道。在T→+∞的极限下,信号是严格恒定的,上述频率消失,并且我们在f=0处有一个趋于无穷大的主项。也就是之前文章中提到的狄拉克δ函数。
练习1:证明持续时间为T的正弦振荡的傅里叶变换是一个以f0为中心的sinc函数,其中该量是振荡频率。最后,验证在T→+∞的极限下,傅里叶变换是以f0为中心的狄拉克δ函数。
结论傅里叶变换框架是同名分析的构成要素。借助分布理论(狄拉克δ函数),可以处理恒定信号和周期信号的病态案例(见练习1),从而将傅里叶级数理论融入其中。

 我要赚赏金
我要赚赏金

