EEPW论坛

01引言

自动驾驶的安全验证是保证系统在给定环境中正确及安全操作的过程。系统的期望行为通过某些规范标准来定义，而系统失败指其行为违反了这些规定。自动驾驶系统由于其复杂性可以认为是一个黑盒系统具备难以探知的特性，故难于理论分析和验证其安全性，而使用暴力遍历方法在复杂的环境中又非常低效。故本文着眼于一个主车行为、环境、交通参与物的行为交互的情景，介绍一种方使用优化算法更高效寻找造成系统被测试系统失败行为轨迹的方法。

本文的第二部分将对文中讨论的问题及用到的符号做出定义，第三部分介绍部分可应用于此类问题的优化算法，最后一部分使用特定的数值实验验证这些方法。

02模型定义

（一）符号定义

ℳ代表被测试系统、ℰ代表环境、A代表交通参与物行为，则对于离散的时刻1到t被测试系统根据对环境的观测o_t做出行为a_｛1:t｝=［a_1,...,a_t］；同时将系统的状态改变为s_｛1:t｝=［s_1,...,s_t］；交通参与物根据环境状态做出干扰行为x_｛1:t｝=［x_1,...,x_t］。元素间的交互可以由下面的等式描述：

a_t=ℳ(o_1:t),x_t=A(s_1:t),s_t+1,o_t+1=ℰ(a_1:t,x_1:t)

则一个具体场景即一条由不同时刻环境状态、主车行为、参与物行为组成的轨迹。本文中我们假设环境和系统（主车）本身不具备不确定性，则干扰车行为是唯一可以影响系统的变量，即环境状态向量s可以表示成干扰行为向量x的函数，即s=f(x)。系统失败可以等价于状态s=f(x)违反了某些规定φ。此时具体场景中的轨迹可以完全由x决定。

（二）问题定义

定义损失函数c(x)满足系统失败等价于c(x) ≦ℰ ，则一个满足c(x) ≦ℰ的扰动轨迹x即为造成系统失败的一个反例。故可以通过优化算法高效索引使c(x)取值最小的扰动轨迹x来寻找反例场景，即falsification任务

x*=argmin｛c(x)｝。

若想考虑寻找最容易发生的失败场景即most-likely failure analysis任务，可以将x发生的概率（或似然/log似然函数）考虑p(x)进损失函数，例如定义

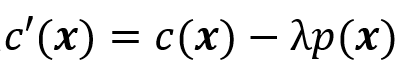
或

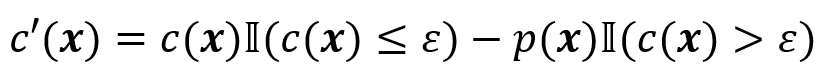
轨迹空间和损失函数的复杂性导致上述优化问题往往存在维度高、多局部最优解、高度非线性、不光滑等问题，进而导致无法通过传统优化算法求解。故能够适应高维空间、跳出局部最优的全局非梯度算法更适合黑盒验证问题。本文剩余部分将以模拟退火算法、遗传算法以及贝叶斯优化为例，介绍这些算法及其应用。

03优化算法介绍

（一）模拟退火算法

将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。模拟退火算法正是一种借鉴了这种现象的随机搜索算法。其优点是不受维度、光滑性等限制，可以高效收敛到最优解，但是模拟退火的一个缺点是对并行计算的支撑较差。该算法的主要过程如下图所示：

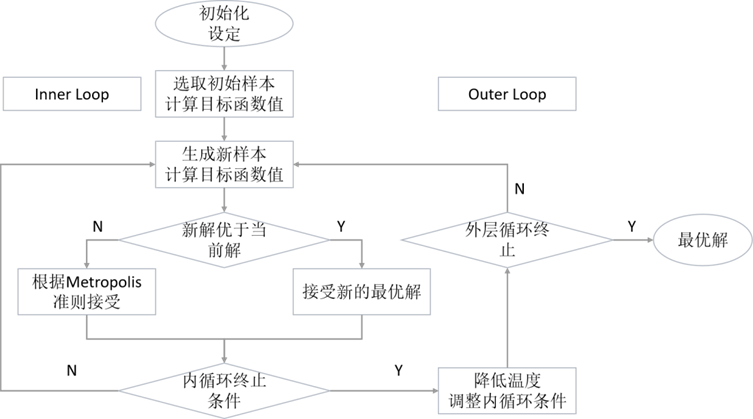
模拟退火算法分为内外两个循环。内循环每次在当前解x附近随机生成一个新的解x*并按照如下的Metropolis准则接受这个新解

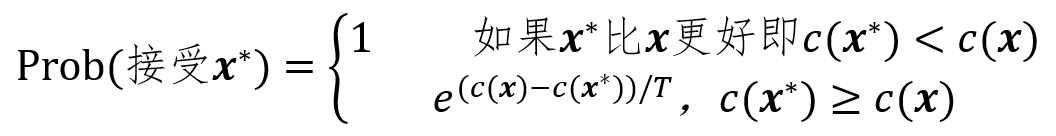
其中T为本循环中的温度。可以看出当温度较高时算法比较容易接受一个更差的解而当温度降低，系统会收敛到附近的最优解。

算法内循环为齐次算法，即每次固定指定L次，负责在当前温度下寻找最优解。外循环负责降温过程，可以按照固定的比例指数下降（基础策略），也可以根据外循环次数减速下降（例如玻尔兹曼策略和柯西策略）。

（二）遗传算法

遗传算法是一种模仿生物自然进化过程寻求全局最优解的方法。此方法不受解空间维度、目标函数光滑性等限制，可以很好的支持并行计算并在一定假设下可以证明收敛到全局最优解。其主要过程如下图所示。

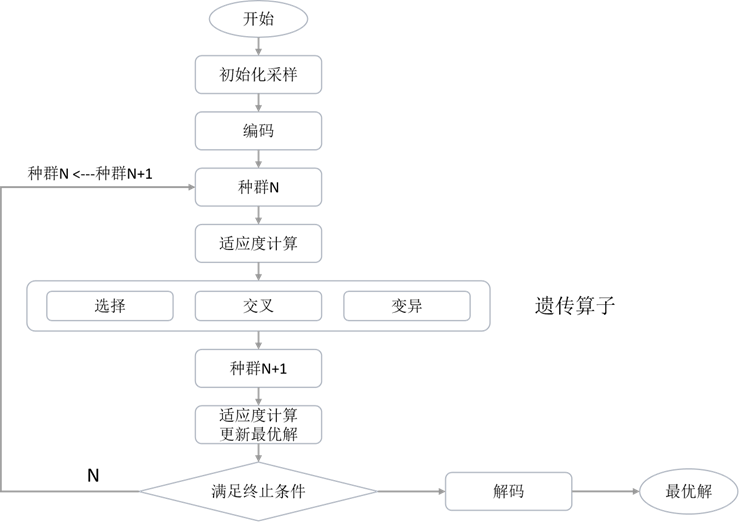
其中：

初始化：一般在解空间中随机选取一定数量的样本作为初代种群；

编码：将解空间转化为编码空间，以便于遗传算进行的过程，转换后解空间中任一点可以转化为一个染色体。常见的编码方式包括二进制、格雷码、实数、符号等编码方式；

适应度：与损失函数关联，评价个体优秀程度的非负函数。

选择--根据适应度从种群中选取比较优秀的样本来生产下一代个体的过程，常见的选择算子包括轮盘赌、随机遍历抽样、排序、锦标赛等；

交叉：通过合并“父母”双方染色体生成下代个体的过程。一般可采用交换父母双方染色体中基因片段的方法，对于排列组合优化问题可以采用匹配交叉、顺序交叉等方法。

变异：在下代个体引入随机突变来丰富种群的多样化。一般以较小的概率随机改变染色体中一个或一部分基因的取值。

（三）贝叶斯优化

贝叶斯优化适应黑盒函数计算复杂并缺少先验知识的情况，同时其允许黑盒系统的输出值存在独立噪声是前面算法不具备的。贝叶斯优化一般采用高斯过程作为代理模型，估计黑盒系统在未观测点取值的分布代替估计其取值。具体来说

1、已知黑盒系统在已有观察点x₁:ₖ=[x₁,x₂,...xₖ]上取值y₁:ₖ=[y₁,y₂,...yₖ]，同时假设此系统取值的先验分布为N(μ₀(x₁:ₖ),Σ₀(x₁:ₖ,x₁:ₖ))，其中μ₀和Σ₀分别为期望向量函数和核函数（协方差矩阵函数）。

2、假设黑盒系统在未观测点x的取值y在x₁:ₖ条件下的后验分布服从正态分布N(μ(x),σ²(x))，则

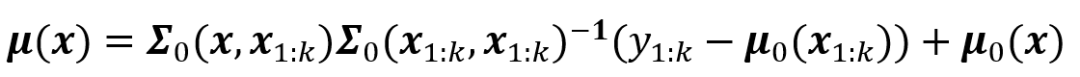
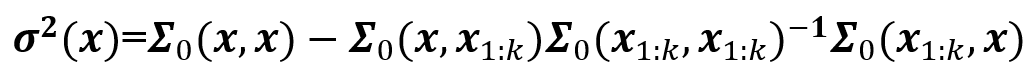
常常令期望向量经常的μ₀=0，而常见的核函数有高斯核（径向基）、Matern核函数、有理二次核等，也可以对不同核函数做线性和生成新的核函数。在确定使用的代理模型（超参数设置）后，贝叶斯优化按照下面的流程寻找黑盒系统的最优值：

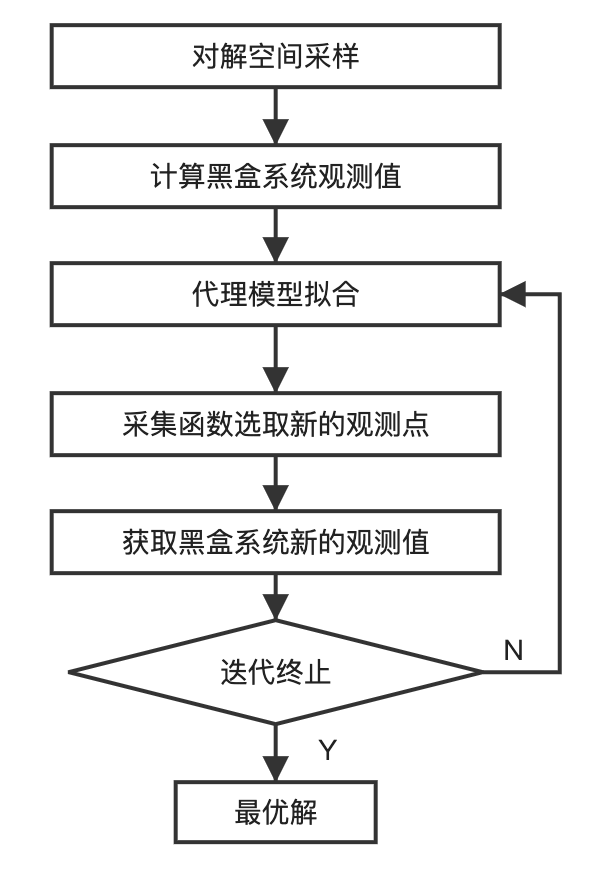
其中采集函数即判断如何选取新观测点的函数，常见的采集函数有最小化期望、最大化标准差、最小的置信区间下界、最大下降概率、最大下降期望等策略。

需要注意的是基础的贝叶斯算法不适应维度很高的情况，这时可以采用信赖域思想构建局部代理模型并配合基于Thomption采样的采集函数来克服高维问题。

04

数值实验

为了方便说明，我们使用一个已知结果的显性函数代替仿真来说明。Generalized Schwefel's Problem是一个经典的多峰函数，使用传统算法求解往往会陷入局部最优。下面以此函数为例，验证上面介绍算法的效果。

具体的目标函数为

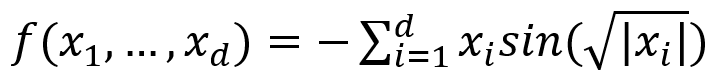
其中取值范围xᵢ∈[-500,500]。当d=2时即2维图像如下：

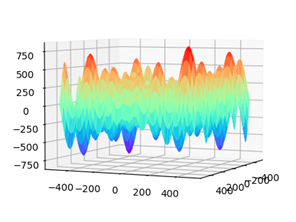
通过图像可以轻松看出此函数属于多峰函数且在原点不可导，其理论最优解当前仅当全部xᵢ=420.9687。在30维空间中目标函数的最小值f*=12569.5，下面将测试不同算法的效果并与梯度算法或随机索引对比

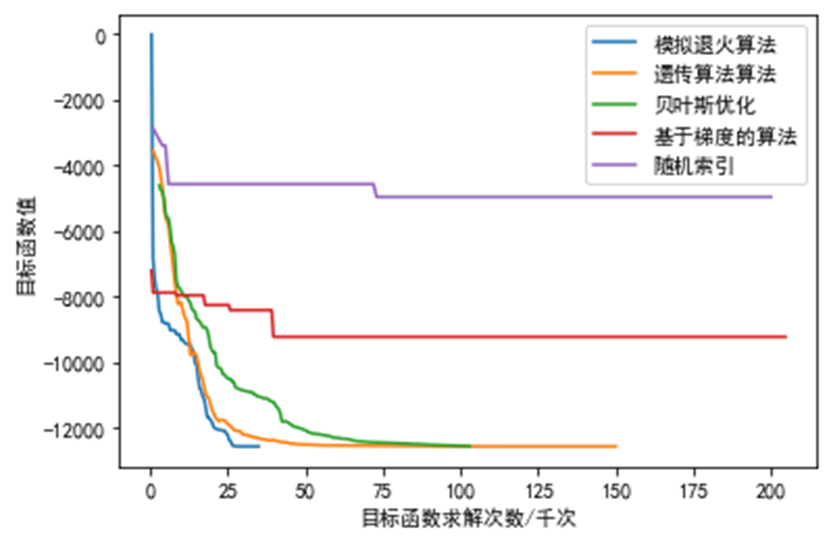
通过上面的图片展示，模拟退火算法、遗传算法、贝叶斯优化算法均可以收敛到全局最优解，而基于梯度的算法或随机索引很难在可接受的时间内寻找到全局最优解。其中模拟退火算法收敛速度最快，单考虑到其对并行能力的欠缺，往往所需时间更长。基于置信域的贝叶斯算法收敛所需的目标函数计算次数低于遗传算法，但随着观测样本越来越多，高斯过程回归的拟合所花费的时间越来越长，故此方法更适合目标函数计算成本非常高的情况。