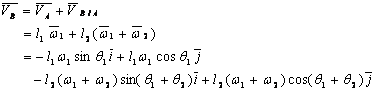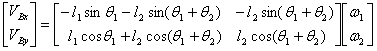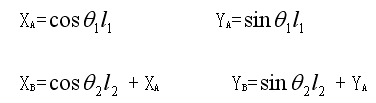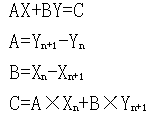根据机器人的运动学分析模型对机器人进行动态仿真是机器人设计过程的一个重要环节。本文对SCARA型机器人进行了运动学分析,建立了该类型机器人的运动学模型,提出了SCARA型机器人避障仿真算法,并对其进行了计算机仿真与分析,这对机器人运动学、动力学、微机控制和路径规划等方面的研究有重要的参考价值。 根据机器人的运动学分析模型对机器人进行动态仿真是机器人设计过程的一个重要环节。本文对SCARA型机器人进行了运动学分析,建立了该类型机器人的运动学模型,提出了SCARA型机器人避障仿真算法,并对其进行了计算机仿真与分析,这对机器人运动学、动力学、微机控制和路径规划等方面的研究有重要的参考价值。
SCARA型机器人仿真避障算法的研究
丛明(1) 金立刚(1) 王崇霞(2)
(1).大连理工大学 机械工程学院,辽宁 大连 116023;(2).威海市职业技术学院 山东 威海 264200
摘 要:根据机器人的运动学分析模型对机器人进行动态仿真是机器人设计过程的一个重要环节。本文对SCARA型机器人进行了运动学分析,建立了该类型机器人的运动学模型,提出了SCARA型机器人避障仿真算法,并对其进行了计算机仿真与分析,这对机器人运动学、动力学、微机控制和路径规划等方面的研究有重要的参考价值。
Evaded the barrier algorithm and its simulation research for a SCARA Robot
CONG Ming JIN Ligang WANG Chongxia
Abstract: In robot design field, carries out a dynamic simulation based on its kinetics analysis model is an emphasis process. This paper analyzed a SCARA robot in kinematics, established its kinematics model, proposed evaded barrier algorithm and achieved its computer analysis simulation, which have significant referenced value in robot kinematics, dynamics, computer control and route layout fields.
关键词:SCARA型机器人;运动学分析;计算机仿真
Key Words: SCARA Robot; Kinematics analysis; Computer aided simulation
1 引言
为了使机器人控制器能精确地控制机器人本体按预定轨迹运动,需要对机器人运动过程进行系统的分析和仿真[1]。以运动学模型为基础的机器人仿真能够真实地再现当前设计中的不足和缺陷,这对优化设计、缩短设计周期、节约成本等方面都有着重要的现实意义。现有的各种仿真方法各有自己的优缺点,Matlab可通过齐次变换矩阵(A矩阵)直接得出位置逆解,但是仿真结果不能形成动画和图形报表,其仿真的结果也不易进行二次开发;Idea-s、Pro/E等大型工程软件虽然可以方便地观察仿真的动态情况,但在动力学和路径控制上灵活性很差,而且此类软件高昂的价格和复杂的操作方法,也从一定程度上降低了仿真的优越性和可操作性性[2]。因此,本文利用Lagrange-Euler方法对SCARA型机器人进行运动学分析,以BASIC语言为基础自行编写一个通用的计算机仿真程序。
2 SCARA型机器人的运动学分析
获得机器人正运动学方程的通用方法是利用Denavit-Hartenberg(简称D-H)模型。D-H模型表示了对机器人连杆和关节进行建模的一种非常简单的方法,可用于任何机器人构型,而不管机器人的结构顺序和复杂程度如何。机器人坐标n相对于n+1的位置及方向齐次变换矩阵为[3]:
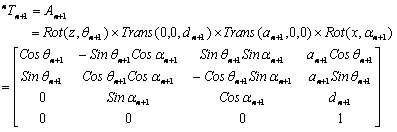
按D-H方法建立SCARA型机器人运动学方程,设定连杆坐标系如图1所示,其相应的连杆参数见表1。其中 为关节变量,相邻两杆件坐标系间的位姿矩阵满足 为关节变量,相邻两杆件坐标系间的位姿矩阵满足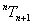 。 。
表1 SCARA型机器人关节参数
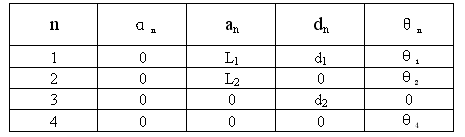
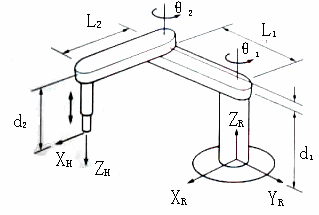
图1 SCARA型机器人的关节坐标系
根据图1和表1,可以得到SCARA型机器人执行末端H对与基座R的总的齐次变换矩阵为:
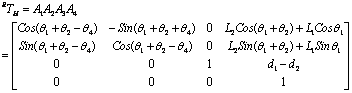 (1) (1)
这样,根据执行末端的位置矢量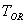 和公式 = 和公式 = 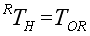 [3],可知SCARA型机器人的运动学逆解为: [3],可知SCARA型机器人的运动学逆解为:
代入(1)式,可得到SCARA型机器人的位置逆解表达式为:
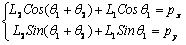 (2) (2)
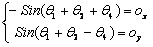 (3) (3)
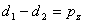 (4) (4)
解(2)式,为:
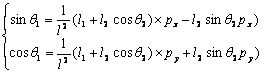 (5) (5)
根据(5)式,得:
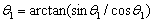 (6) (6)
解两水平臂所形成的三角形,为:
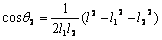 (7) (7)
根据(7)式,得:
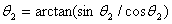 (8) (8)
解(3)式,为:
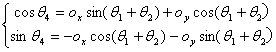 (9) (9)
根据(9)式,得:
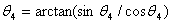 (10) (10)
解(4)式,得:
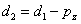 (11) (11)
其中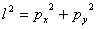 , 为末端执行器与基座在水平方向上的距离。 , 为末端执行器与基座在水平方向上的距离。
根据上述的位置逆解,该SCARA型机器人的速度逆解为:
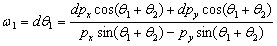 (12) (12)
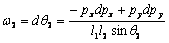 (13) (13)
 (14) (14)
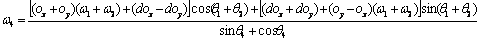 (15) (15)
3 SCARA型机器人的运动学仿真
SCARA型机器人最显著的特点是它在x-y平面上的运动具有较大的柔性,而沿z轴具有很强的刚性[3]。所以,SCARA型机器人运动控制的重点在两个串联关节的旋转变量上,也就是图1中标出的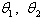 。在本文中,也着重对SCARA型机器人上的两个串联旋转关节进行仿真。 。在本文中,也着重对SCARA型机器人上的两个串联旋转关节进行仿真。
3.1 SCARA型机器人仿真的模型和变量说明
SCARA型机器人运行时需要控制的物理参数有四个,分别是 。其中 。其中 为唯一一个直线变量,控制空间垂直变化; 为唯一一个直线变量,控制空间垂直变化;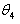 则是为实现末端执行器在空间中的绝对位置,其大小满足 则是为实现末端执行器在空间中的绝对位置,其大小满足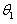 、 、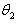 两角度的线形关系,因此如何实现机械臂的预定运动将通过控制 两角度的线形关系,因此如何实现机械臂的预定运动将通过控制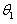 与 与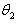 来实现。 来实现。
图2为SCARA型机器人平面串联关节的示意图,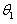 表示第一关节相对参考坐标系的旋转角度, 表示第一关节相对参考坐标系的旋转角度, 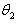 表示第二个关节相对第一关节的旋转角度。 表示第二个关节相对第一关节的旋转角度。 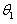 与 与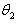 的数值可以通过位于关节处的伺服电机精确控制,这样,B点在参考坐标系中的任意x-y平面上的位置均可以确定[4][5]。 的数值可以通过位于关节处的伺服电机精确控制,这样,B点在参考坐标系中的任意x-y平面上的位置均可以确定[4][5]。
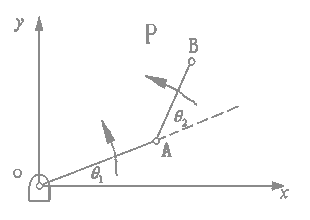
图2 SCARA型机器人串联关节示意图
根据图2及机器人位置逆解,B点的速度为:
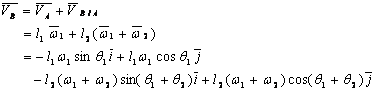
又由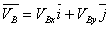 可将速度方程写成矩阵形式,为: 可将速度方程写成矩阵形式,为:
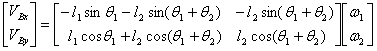
根据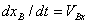 , , 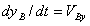 及 及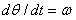 ,可得到机器人串联关节的微分运动关系为: ,可得到机器人串联关节的微分运动关系为:

它是进行机器人仿真的数学基础,并可根据此式得到SCARA型机器人的雅可比矩阵,为:
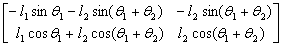
3.2 SCARA型机器人的运动动态仿真
根据机器人的位置逆解和微分运动关系,可在Visual Basic环境利用绘图函数再现机器人的运动过程。具体方法如下:
①. 分析运动轨迹;
②. 将运动轨迹函数化;
③. 通过位置逆解将运动轨迹上的每一点映射成角度控制参数;
④. 根据角度参数绘图。
在机器人的控制过程,经常需要机器人进行匀速运动以实现特殊的操作,如喷漆、焊接等作业,根据上述方法可得到机器人在x-y平面内按x方向匀速运动(如图2中的箭头P方向)的动态仿真的源程序[6][7][8](详见附录)。
程序输出结果如图3所示:
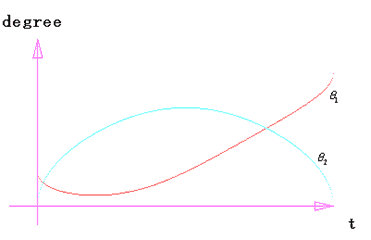
图3 仿真结果(x方向)
其中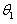 , ,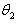 的“角度―时间”表已经记录到文本文件中,此角度表完全可以通过接口程序导入到机器人控制器中来实现B点的预期直线运动。 的“角度―时间”表已经记录到文本文件中,此角度表完全可以通过接口程序导入到机器人控制器中来实现B点的预期直线运动。
值得说明的是,在上述例子中,更改B点的运动轨迹函数即可实现不同运动轨迹的“角度―时间”图表。B点沿y方向运动,按圆弧运动均以编译通过(如图4所示)。这样,就已经完成了空间运动轨迹的基本分析,当需要实现直线及有限次几何曲线的运动时,可利用调用或迭代等算法将基本的直线或圆弧轨迹函数映射为目标轨迹函数。
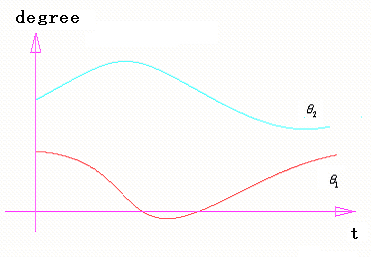
图4 仿真结果(B点做圆周运动)
3.3 SCARA型机器人运动动态仿真结果的应用
利用运动的动态仿真结果,可以对机器人的运动进行避障模拟,来计算机器人在运行过程中对某一障碍区域的安全移动范围,具体的方法是:
①. 通过已知的运动角度计算点A、点B的坐标。公式如下:
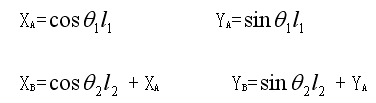
②. 用数学的线性函数将连续的障碍区间离散成若干条首尾相连的封闭线段组。
如图5所示,设C为障碍区域,在C域附近取若干点(图中为N1,N2,N3,N4,N5),首
尾连接成一个多边形。
设第N条线段的端点坐标为Nn(Xn,Yn),Nn+1(Xn+1,Yn+1), 则此条线段(边)的方程为:
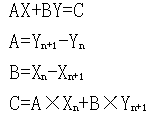
③. 讨论多边形每边构成的线段是否与机器人移动臂所在直线存在交点。
设两条线段的方程为:
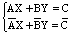
写成矩阵形式为:
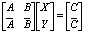
如果矩阵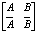 存在,则存在交点。 存在,则存在交点。
④. 如果交点存在,再判断交点是否在直线上。具体的方法是联解由这两条直线的方程所组成的方程组,方程组的解就是交点的位置坐标。
交点位置坐标解为:

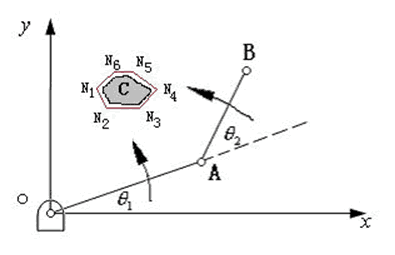
图5 结果的应用
通过上述过程就实现了对障碍区进行模拟分析,在机器人硬件控制上,对交点的判断接口即可作为传感器信号的引入点,用以保证机器人在遇到障碍时能做出相应的避让动作。
4 结论
对机器人进行运动学分析和仿真,能很好地反映机器人机构设计情况。特别是需要机器人实现预期的运动轨迹时,机器人运动仿真这一一般性方法能真实地再现运动情况,具有效率高、可视性强等特点。但是,由于仿真的模型是建立在运动学和数学基础上的,缺少机器人自身中质量分布、质量大小、控制响应时间等诸多物理参数的限制,在精度方面,特别是重复定位精度方面距离实际还存在一定的偏差。
|
 我要赚赏金打赏帖
我要赚赏金打赏帖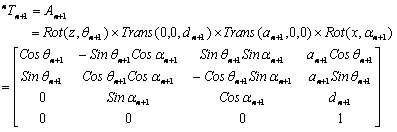


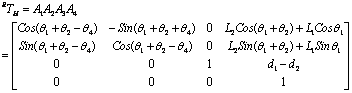 (1)
(1)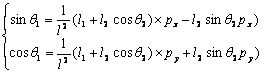 (5)
(5)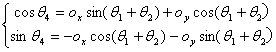 (9)
(9)