EEPW论坛

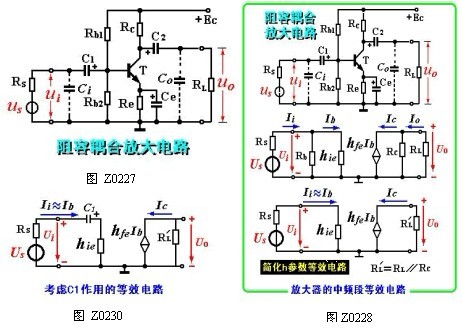
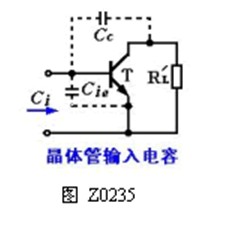
单级共射阻容耦合放大电路如图Z0227所示。在图Z0235中，Cie（Cbe）、Cc（Cbc）。分别表示晶体管的发射结和集电结的等效电容，一般为几pF～几百pF。

一、中频段

中频段放大电路的微变等效电路如图Z0228所示。输入耦合电容C1、输出耦合电容C2及射极旁路电容Ce因其容量较大，容抗较小，在中频段可视为短路；而输入、输出回路的分布电容Ci、Co及电容Cie 、Cc 容量较小，容抗较大，在中频段可视为开路。由此可得出中频段放大电路的电压放大倍数为：

它表明，在中频范围内，Au和φ均为常数，与频率无关。

二、低频段

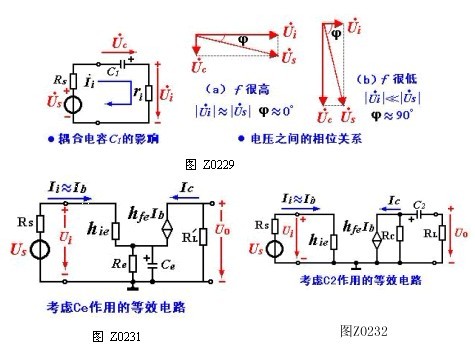
在低频范围内，C1、C2 及Ce容抗增大，不能忽略。Ci、Co及电容Cie 、Cc 的容抗很大仍可视为开路。此时的微变等效电路如图 Z0229、Z0230、Z0231、Z0232所示。

由图可知，随着频率的不断降低，C1、C2 及Ce 的容抗增大，使减小，减小，导致输出减小，从而使放大倍数降低。此外，频率越低，C1、C2 及Ce造成的附加相移越小，当f→0时，附加相移接近 -90°。

在实用电路中，常选取C1＝C2（5～20）μF，Ce ＝（50～200）μF，基本上可满足一般低频放大电路对下限频率的要求，消除低频时的失真。

三、高频段

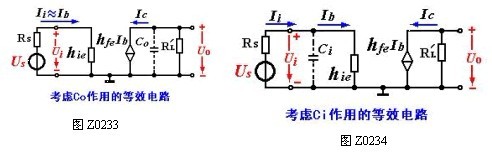
放大电路在高频段时也可惜助h参数微变等效电路来分析，其徽变等效电路如图Z0233、Z0234所示。C1、C2 及Ce的容抗较小均可视为短路，而Ci、Co及电容Cie、Ce的容抗也较小，其分流作用不可忽略。且这种影响随着频率的增高更加明显。同时，它们引起的附加相移也随着频率的增高而增大，当f → ∞时，附加相移接近 - 270°。

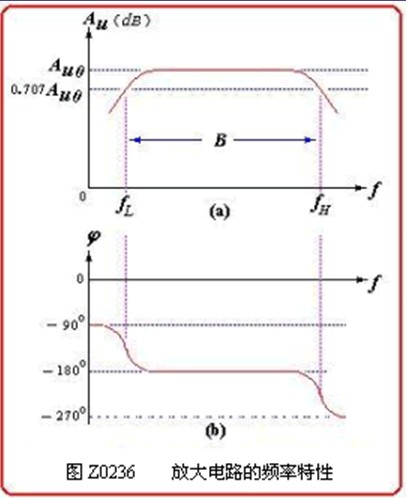
单级阻容耦合放大电路总的频率特性曲线如图Z0236所示。

因为功率与电压的平方成正比，所以在工程计算上规定，电压放大倍数的幅值下降到中频幅值Auo的0.707倍时所对应的频率称为半功率点频率（电压放大倍数下降到Auo 的0.707 倍时，相当于功率卞降一半。在幅频特性曲线上，低频端和高频端各有一个半功率点，其相应的半功率点频率称为下限频率fL和上限频率fH 。半功率点的电压放大倍数

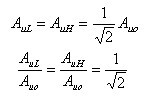
用分贝表示

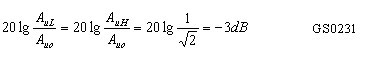
可见，半功率点的电压放大倍数比中频段 的电压放大倍数Auo衰减了3dB。我们定义fH与fL之间的频率范围为放大电路的通频带并以B表示，即

B = f H－ f L GS0232

在通频带内，由于输出功率的减少不会超过中频区的一半，附加相移不超过45°，因而人耳感觉不到明显变化，这样就可以认为在通频带B内放大电路基本上没有频率失真。

通频带内的区域称为中频区；频率低于下限频率 f L 的频域称为低频区，频率高于上限频率f H 的频域叫高频区。

在分析放大电路的频率特性时，为了在有限的数轴上，描绘较大范围的频率变化对放大倍数的影响，通常采用对数频率特性曲线。这时横轴采用lgf，纵轴采用分贝，即201g | Au |（幅频特性），或φ的数值（相频特性）。对数频率特性又叫波特图。

放大倍数用分贝表示的优点是：可避免放大倍数的庞大数字并可以把放大倍数的乘法运算简化为加法运算；对数的单位比较符合听觉器官对声音感觉的特性；便于绘制频率特性的对数坐标图。