EEPW论坛

实现模2除法的线路

　　循环校验码的核心逻辑线路是实现模2除的线路。按照前面介绍的方法，可将模2除的步骤分解归纳为两种操作：如果被除数或者余数最高位的值为0，直接将余数左移一位；如果被除数或部分余数最高位的值为1，用生成多项式G(x)作模2减，然后余数左移一位。

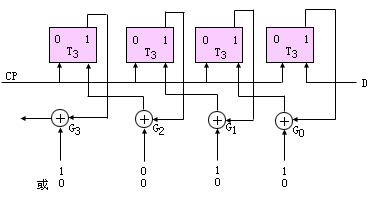
图2.2 实现模2除的逻辑图
　　对前述用G(x)=1011产生(7,4)校验码的例子，可采用图2.2所示线路，产生3位的余数。图中的模2减用异或门实现，左移一位由移位寄存器实现；用异或门的输出控制左边一位寄存器的D输入端，可同时实现模2减和左移。用最左一位的取值控制是否做模2减，当其为1时，减去的数就是生成多项式G(x)=1011。这里，被除数D是逐位串行送到移位寄存器的，且由CP脉冲同步。




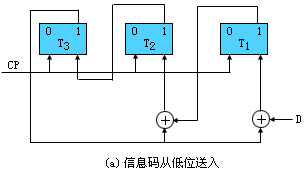
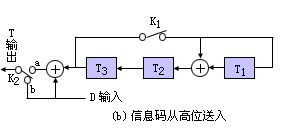
图2.3 实现G(x)=1011的线性(7,4)分组码模2除线路图
　　由于G(x)固定不变，故G2可省去；只求三位余数，故G3和T0也失去意义。图2.2可简化为图2.3(a)。
对图2.3(a)的线路来说，在发送端，输入信息码D为1100，串行从低位送入，先左移三位形成1100000，再通过7步模2除，可在移位寄存器 T₃ T₂ T₁ 中得到余数010；在接收端，对7位的CRC码字1100010，执行7步模2除之后，若在 T₃ T₂ T₁ 得到000，表明CRC码字中无任何一位出错；若余数不为全0，可根据表2.4确定出错位置。

　　设T_i为T3T2T1某触发器当前状态，T_i'为次态，可用次态方程表示图2.3(a)的模2除电路： T_3'=T₂, T_2'=T₃⊕T₁ , T_1'=T₃⊕D。
分别用被除数1100000和1010000验证取得余数为010和011的工作过程，见表2.6。读者可用模2除竖式计算各步结果并与之比较。
表2.6 图2.3(a)线路工作过程举例

步骤	信息码1100	信息码1010
	输入D TTT	输入D TTT
初态 1 2 3 4 5 6 7	0 　000 　1 　001 　1 　011 　0 　110 　0 　111 　0 　101 　0 　001 　0 　010	0 　000 　1 　001 　0 　010 　1 　101 　0 　001 　0 　010 　0 　100 　0 　011

　　可以将图2.3(a)的线路稍加变化，即得到图2.3(b)的线路，用作为G(x)=1011的系统线性(7,4)分组码的编码线路。待编码信息D由高位端送入，CRC码由T送出。开始时，开关K₁闭合，K₂打到b位置，输入信息进入除法线路的同时送到T输出。经过4步之后,T₃T₂T₁即为余数。然后，K₁断开，K₂打到a，T₃T₂T₁只有移位功能，正好将余数拼接在信息码后经T送出。图2.3(b)中，开关K₁闭合，K₂打到b，T₃T₂T₁及输出T可表达为: T=b=D， T_3' =T₂ , T_2' =T₁⊕T₃⊕D, T_1'=T₃⊕D 。 当开关K₁断开，K₂打到a，T₃T₂T₁及输出T可表达为: T=a=T₃⊕D=T₃(D为0)， T_3'=T₂， T_2' =T₁， T_1' =0。信息码为1100和1010取得的CRC码1100010和1010011的工作过程见表2.7。

表2.7 图2.3（b）线路编码过程举例

步骤	信息码1100	信息码1010
	输入D TTT 输出T	输入D TTT 输出T
初态 1 2 3 4 5 6 7	0 　000 　0 1 　011 　1 1 　101 　1 0 　001 　0 0 　010　 0 0 　100 　0 0 　000 　1 0 　000 　0	0 　000 　0 1 　011 　1 0 　110 　0 1 　100 　1 0 　011 　0 0 　110 　0 0 　100 　1 0 　000 　1