EEPW论坛

模拟电路网络课件 第三十五节:负反馈放大电路的稳定问题

7.5 负反馈放大电路的稳定问题

一、产生自激振荡的原因与条件

交流负反馈能够改善放大电路的许多性能，且改善的程度由负反馈的深度决定。但是，如果电路组成不合理，反馈过深，反而会使放大电路产生自激振荡而不能稳定地工作。

1. 产生自激振荡的原因

前面讨论的负反馈放大电路都是假定其工作在中频区，这时电路中各电抗性元件的影响可以忽略。按照负反馈的定义，引入负反馈后，净输入信号 在减小，因此， 与 必须是同相的，即有 ，n = 0，1，2…（ 、 分别是、的相角）。可是，在高频区或低频区时，电路中各种电抗性元件的影响不能再被忽略。、是频率的函数，因而 、的幅值和相位都会随频率而变化。相位的改变，使和不再同相，产生了附加相移（ ）。可能在某一频率下，、的附加相移达到即 ，这时，与必然由中频区的同相变为反相，使放大电路的净输入信号由中频时的减小而变为增加，放大电路就由负反馈变成了正反馈。当正反馈较强以致 ，也就是时，即使输入端不加信号（ ），输出端也会产生输出信号，电路产生自激振荡。这时，电路会失去正常的放大作用而处于一种不稳定的状态。

2．产生自激振荡的相位条件和幅值条件

由上面的分析可知，负反馈放大电路产生自激振荡的条件是环路增益

它包括幅值条件和相位条件，即

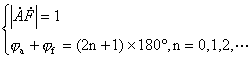
为了突出附加相移，上述自激振荡的条件也常写成

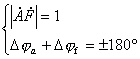
的幅值条件和相位条件同时满足时，负反馈放大电路就会产生自激。在 及时，更加容易产生自激振荡。

二、稳定性的定性分析

根据自激振荡的条件，可以对反馈放大电路的稳定性进行定性分析。

设反馈放大电路采用直接耦合方式，且反馈网络由纯电阻构成，为实数。那么，这种类型的电路只有可能产生高频段的自激振荡，而且附加相移只可能由基本放大电路产生。在这样的条件下，对于由一只管子组成的负反馈放大电路来说，因其产生的最大附加相移（ ）为-90°，相位条件不能满足，故不可能产生自激振荡。在两级直接耦合的负反馈放大电路中，当频率从零变化到无穷大时，附加相移 可以从0°变化到-180°。虽然从理论上存在满足相位条件 =-180°的频率fo，但fo已趋于无穷大，而且当 时，已为零，即幅值条件不能满足，所以也不可能产生自激振荡。而在三级直接耦合的负反馈放大电路中，当频率从零变化到无穷大时，附加相移可以从变化到-270°，因而存在使=-180°的频率fo，而且当时，>0，有可能满足幅值条件，所以可能产生高频自激振荡，可以推知，超过三级以后，放大电路的级数越多，引入负反馈后越容易产生高频自激振荡。因此，实用电路中以三级放大电路为最常见。

与上述分析相类似，放大电路中耦合电容、旁路电容等越多，引入负反馈后就越容易产生低频自激振荡。而且越大，幅值条件越容易满足。

三、稳定性的判定

由自激振荡的条件可知，如果环路增益 的幅值条件和相位条件不能同时满足，负反馈放大电路便不会产生自激振荡。所以，负反馈放大电路稳定工作的条件是：当=1时，，或当时，1。

工程上常用环路增益的波特图分析负反馈放大电路能否稳定地工作。

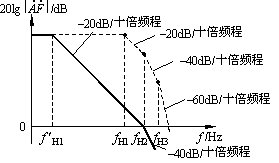
1．判断方法

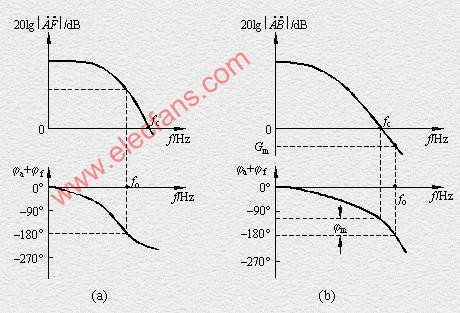
图1(a)、(b)分别是两个直接耦合式负反馈放大电路的环路增益的波特图。图中fo是满足相位条件 时的频率，fc是满足幅值条件时的频率。

在图1(a)所示波特图中，当f =fo，即时，有，即 ，说明相位条件和幅值条件能同时满足。同样，当f =fc，即dB， 时，有。所以，具有图1(a)所示环路增益频率特性的负反馈放大电路会产生自激振荡，不能稳定地工作。

在图1(b)所示波特图中，当f =fo，即时，有，即 ；而当f =fc，dB，即时，有。说明相位条件和幅值条件不会同时满足。具有图1(b)所示环路增益频率特性的负反馈放大电路是稳定的，不会产生自激振荡。

综上所述，由环路增益的频率特性判断负反馈放大电路是否稳定的方法是：比较fo与fc的大小。若fo>fc，则电路稳定；若fo≤fc，则电路会产生自激振荡。

2. 稳定裕度

根据上面讨论的负反馈放大电路稳定性的判断方法知，只要fo>fc，电路就能稳定，但为了使电路具有足够的稳定性，还规定电路应具有一定的稳定裕度，包括增益裕度Gm和相位裕度jm

。

（1）增益裕度Gm

定义f =fo时所对应的20lg的值为增益裕度Gm，如图1(b)所示幅频特性中的标注。Gm的表达式为

稳定的负反馈放大电路的，且要求Gm≤–10dB，保证电路有足够的增益裕度。

（2）相位裕度jm

相位裕度jm定义为

式中fc是dB时的频率，是 f =fc时的相移，如图1(b)所示相频特性中的标注。

稳定的负反馈放大电路的jm>0，且要求jm≥45°，保证电路有足够的相位裕度。

总之，只有当Gm≤–10dB且jm≥45°时，负反馈放大电路才能可靠稳定。

当负反馈放大电路中的反馈网络是由纯电阻构成时，反馈系数的大小为一常数，同时有jf =0。这种情况下，可以利用开环增益的波特图来判别反馈放大电路的稳定性。下面以例说明。

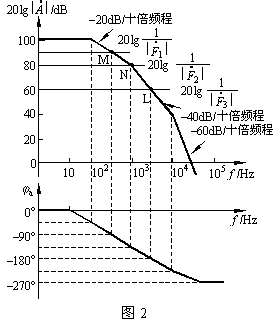
设有一反馈网络由纯电阻构成的反馈放大电路，其开环增益的幅频特性曲线如图2中的折线所示。由于反馈系数F为常数，因此，自激振荡的幅值条件可写成 的形式。同样，可写成 的形式。于是，可在开环增益的幅频特性坐标中作出高度为 的水平线（称为反馈线），在它与 的幅频特性曲线的交点处必然满足 即的幅值条件，这时再根据该交点所对应的相移是否小于180°来判断电路是否稳定。由此可以断定，在与图2相对应的负反馈放大电路中，当取反馈系数 及 时， 均小于180°，电路是稳定的。而当 （ 大于 及 ）时，对应的ja=–180°，此时电路会产生自激振荡。

上述分析说明，负反馈越深，放大电路越容易产生自激振荡。因此，设计这种负反馈放大电路时，一般应使水平线(反馈线）与的幅频特性曲线相交于斜率为–20dB/十倍频程的线段上，这时有≤135°,能保证设计的负反馈放大电路稳定地工作。

四、自激振荡的消除方法

1、滞后补偿法

发生在放大电路中的自激振荡是有害的，必须设法消除。最简单的方法是减小反馈深度，如减小反馈系数，但这又不利于改善放大电路的其他性能。为了解决这个矛盾，常采用频率补偿的办法（或称相位补偿法）。其指导思想是：在反馈环路内增加一些含电抗元件的电路，从而改变的频率特性，破坏自激振荡的条件，例如使 ，则自激振荡必然被消除。

频率补偿的形式很多，下面先介绍滞后补偿。设反馈网络为纯电阻网络。

滞后补偿是在反馈环内的基本放大电路中插入一个含有电容C的电路，使开环增益的相位滞后，达到稳定负反馈放大电路的目的。

1. 电容滞后补偿

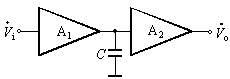
图a,b

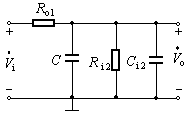
图c

由前面的分析及稳定裕度的要求可知，若 的幅频特性曲线在0dB以上只有一个转折频率（拐点），且下降斜率为–20dB/十倍频程，则属于只有一个RC回路的频率响应，最大相移不超过–90°。若在它的第二个转折频率（拐点）处对应的 ，且此处的最大相移为–135°(有45°的相位裕度)，这样的负反馈放大电路是稳定的，因此电容滞后补偿即按此思路进行。

这种补偿是将电容并接在基本放大电路中时间常数最大的回路里，即前级的输出电阻和后级的输入电阻都比较大的地方，如图1（a）所示。图1（b）是该补偿电路的高频等效电路。其中Ro1前级的输出电阻，Ri2为后级的输入电阻，Ci2为后级的输入电容。未加电容前该反馈放大电路环路增益的幅频特性如图1(c)中的虚线所示，此时的上限频率为

加补偿电容C后的上限频率为

只要选择合适的电容C，使得修改后的幅频特性曲线上，以–20dB/十倍频程斜率下降的这一段曲线与横轴的交点刚好在第二个转折频率fH2处，此处的 ，如图1（c）中的实线所示，此时的（ja+jf）趋于–135°，即 ，且保证jm≥45°，所以负反馈放大电路一定不会产生自激振荡。

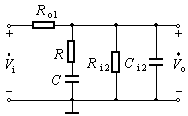
2. RC滞后补偿

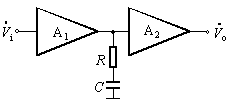a

b

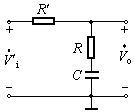c

电容滞后补偿虽然可以消除自激振荡，但使通频带变得太窄。采用RC滞后补偿不仅可以消除自激振荡，而且可使带宽得到一定的改善。具体电路如图2（a）所示，图（b）是它的高频等效电路。通常应选择 ，C≥Ci2，所以可将图（b）简化为图（c）的形式，其中 ，

它的电压传输函数为

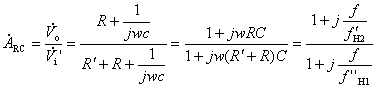
式中 = ，

设未加RC补偿电路前，反馈放大电路的环路增益的表达方式为

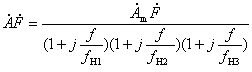
其幅频特性如图2（d）中虚线所示。

只要选择合适的RC参数，使 ，那么加入RC补偿电路后，环路增益的表达式即变为

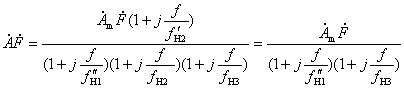
此式说明，加入RC补偿电路后，环路增益的幅频特性曲线上只有两个转折频率，而且如果 的选择，使得修改后的幅频特性曲线上以–20dB/十倍频程斜率下降的这一段曲线与横轴的交点刚好在fH3处，此处的 ，如图2（d）中实线②所示，此时的（ <