EEPW论坛

分段线性化法是将特性曲线分为若干段，每段用直线近似，这样每段中的伏安特性用直线方程表示或用等值线性电路表示，使分析计算大为简化。分段线性化法的分析与计算可分为两种方法：①折线方程；②等值电路法。

一、 折线方程法

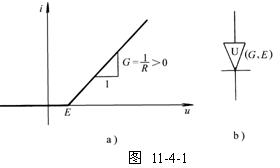
回忆图11-2-2a电路，如二极管VD是理想的，总伏安特性如图11-2-2d所示。将曲线的u、i轴互换，特性如图11-4-1a所示，称为凹形电阻特性，用图11-4-1b表示其符号（图11-2-4c的特性是凸形电阻特性）。

图11-4-1a的电流可表示为：

（11-4-1）

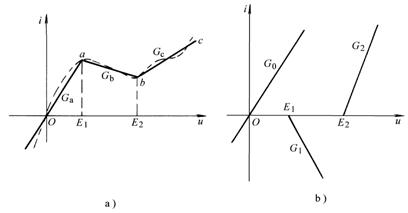
图 11-4-2

图11-4-2a虚线所示的电阻特性曲线可由三段直线Oa、ab、bc近似表示，这三段直线又可用图11-4-2b中的一个线性电阻G₀和两个凹形电阻、的曲线相加而成。 对于：电导

对于：电导（G_b为负，G₁也为负）

对于；电导 （11-4-2）

已知、、Gc（从图11-4-2a中得到），联立求解以上三式得：

（11-4-3）

于是：

（11-4-4）

整理得：

（11-4-5）

式中：

（11-4-6）

式（11-4-5）称为规范化分段线性方程。

例11-4-1 图11-4-3a所示电路，电源的电动势，内阻，与隧道二极管T连接，后者的特性可用三段近似直线表示（图11-4-3b），求工作点。

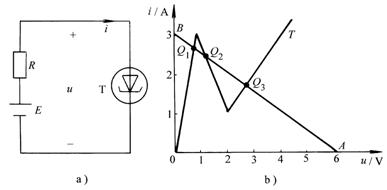
图 11-4-3

解：对照式（11-4-5）、（11-4-6）可知：

；

从式（11-4-3）得：

从式（11-4-6）得：

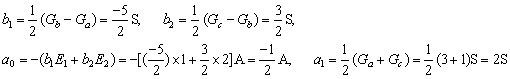
将各数据代入式（11-4-5），得到规范化分段线性方程：

（11-4-7）

为求电路中的电流i和电压u，再列出电源的外特性方程：

（11-4-8）

现用解析法求解，即联立求解式（11-4-7）和式（11-4-8）。当时，式（11-4-7）成为：

（11-4-9）

联解式（11-4-8）、式（11-4-9）得：

当时，式（11-4-7）成为：

（11-4-10）

联解式（11-4-8）、式（11-4-10）得：

当时，式（11-4-7）成为：

（11-4-11）

联解式（11-4-8）、式（11-4-11）得：

二、等效电路法

等效电路法是将给定的非线性曲线用线性电阻、直流电源和理想二极管组成的等效电路表示，这样，非线性电阻电路化为含理想二极管的等效准线性电阻电路，便于分析计算。

图11-4-2a的非线性电阻特性曲线用折线表示后，等值电路如图11-4-4所示。

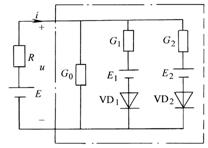
图 11-4-4

现用等效电路法重新计算例11-4-1中隧道二极管的电压和电流。利用该题数据：E=6V，R=2W，E₁=1V，E₂=2V，G₀=3S，G₁= -5S，G₂=3S。

当时，二极管VD₁、VD₂断开，电路成为E、R、G串联，此时：

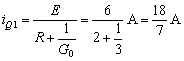
当时，VD₁导通、VD₂断开，利用节点电压法：

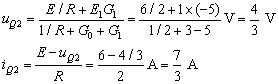
当时，VD₁、VD₂都导通，利用节点电压法：