EEPW论坛

在电子电路中遇到的非线性电路，不仅有作为偏置电压的直流电源U₀作用，同时还有随时间变化的输入电压u_S(t)作用。如果在任何时刻有，则把u_S(t)称为小信号电压。分析这类电路，可以采用小信号分析法。

小信号分析法是一种线性化方法。这一方法的基本思路是在静态工作状态下，将非线性电阻电路的方程式线性化，得到相应的可以用来计算小信号激励所产生响应的线性化电路和线性方程，然后就可以用分析线性电路的方法去进行分析和计算。

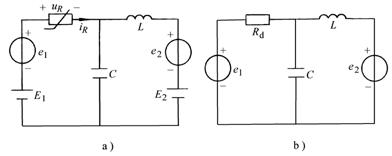
图 11-3-1

某网络如图11-3-1a）所示，L、C是线性的，是压控型非线性电阻，、是直流电压源，时变信号和满足。

各支路电流与各回路电压满足KCL和KVL，即：

（11-3-1）

将i，u表示为，，其中I_e、U_e是只有直流电源作用时的电流、电压，di、du是由小信号电源产生的电流增量和电压增量。

由于：

（11-3-2）

式（11-3-1）减式（11-3-2）得：

（11-3-3）

即由小信号产生的电流、电压增量也满足KCL和KVL。

设非线性电阻是流控型的，其特性为：

当仅有直流电源时，，U_Re、I_Re分别是直流电源作用下非线性电阻的电压和电流。当同时存在小信号电源作用时，将U_Re附近的u_R表示为：

将上式的f(i_R)在I_Re附近展开为台劳级数，得：

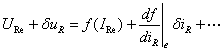
在上式中略去高阶小项，并注意到，整理得等效小信号方程为：

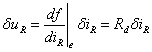（11-3-4）

式中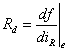，。称为平衡点附近的等效动态电阻。

除了对非线性电阻可以在直流工作点附近作小范围线性化处理外，对非线性电感和电容也可以作同样的处理。设非线性电感是流控型的，其特性为：

即磁链是电流的非线性函数，其电感电压。

当有小信号电源作用时，将Y表示为：

将g(I_L)在I_Le附近展开为台劳级数：

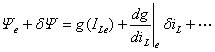
略去高阶项，整理得：

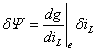
电感电压为：

故：

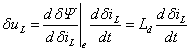（11-3-5）

式中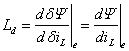，称为平衡点（或直流工作点）附近的等效动态电感。

同理，设非线性电容特性为压控型的，其特性为：

仿照关于动态电感的推导，可得小信号方程为：

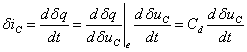（11-3-6）

式中，是平衡点（或直流工作点）附近的等效动态电容。

对于四种非线性受控源，也可推出其小信号等效元件。如图11-3-2a中VCCS的特性为i₂=f(u₁)，当仅有直流电源时，I_2e=f(U_1e)，I_2e、U_1e各为直流电源下的非线性VCCS的电流和电压。

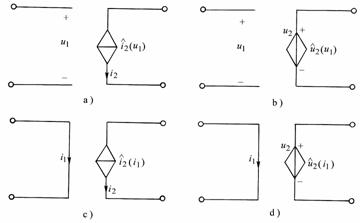
图 11-3-2

当有小信号电源作用时，将在I_2e附近的i₂表示为：

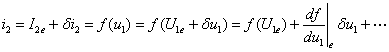
整理得：

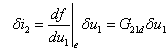（11-3-7）

式中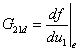，称为VCCS在平衡点附近的等效动态控制系数。

同理可推导其他三种非线性受控源的小信号电路，例如对于图11-3-2d中CCVS的小信号方程为：

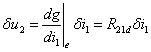（11-3-8）

式中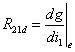，称为CCVS在平衡点附近的等效动态控制系数。

可以看出，式（11-3-4）至式（11-3-8）都是线性方程。对于非线性电路，列出的电路方程是非线性代数方程或者非线性微分方程，这些非线性方程在小信号分析中，都化为含的线性方程，这些动态电阻、动态电感、动态电容，对于小信号di和du来说都是常数。当小信号是正弦波形时，如欲求其小信号稳态响应，则其小信号等效电路与第三章正弦稳态下的R、L、C电路相似，故可用复数方程求解，正弦稳态电路的各种方法都适用。得到di和du后，再求总的。

例11-3-1 图11-3-1a电路中，设直流电源E₁=3V，E₂=1V，正弦电源，e₂=0，L=0.6H，C=0.05F，非线性电阻特性为，求i_R的稳态解。

解：，满足小信号条件。先求只有直流电源E₁、E₂激励下的电路响应（即平衡点），此时，电感短路、电容开路。

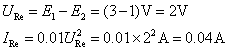
动态电导：

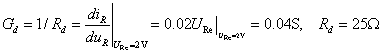
在小信号等效电路图11-3-1b中，e₁是正弦信号，求稳态解可用复数计算。

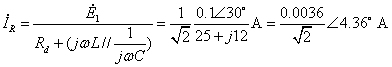
故小信号电流为。

总电流的稳态值为，其中正弦分量的幅值0.0036A小于直流分量0.04A的10倍，故可作为小信号处理。