EEPW论坛

电路中最重要的两个定律是基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL），其表达式为：

KCL： ， KVL：

对两个定律的方程式作拉普拉斯变换，即有：

KCL： ，KVL：

上面两式就是基尔霍夫定律的复频域（s域）形式。这说明各支路电流的象函数仍遵循KCL；回路中各支路电压的象函数仍遵循KVL。

下面介绍各电路元件的复频域（s域）模型，也称运算电路模型。

一、线性电阻元件

图9-4-1（a）表示线性电阻元件的时域模型，当其电压电流参考方向选为一致时，其电压、电流的关系是：

经拉普拉斯变换得电压、电流象函数间的关系：

（式9-4-1）

因此，电阻复频域（s域）模型如图9-4-1（b）所示。

二、线性电感元件

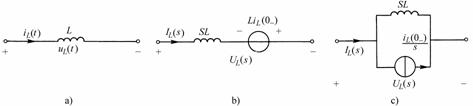
图9-4-2

图9-4-2（a）表示线性电感元件的时域模型，当其电压电流参考方向一致时，电压电流的时域关系式是：

经拉普拉斯变换后得：

（式9-4-2）

根据（式9-4-2）可以画出电感元件的复频域模型，如图9-4-2(b)所示，其中sL称为电感的运算感抗，取决于电感电流的初始值，称为附加运算电压。

三、线性电容元件

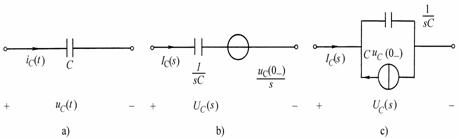
图9-4-3

图9-4-3(a)表示线性电容元件的时域模型，当其电压电流参考方向一致时，电压电流的时域关系式是：

经拉普拉斯变换后得：

（式9-4-3）

根据（式9-4-3）可以画出电容元件的复频域模型，如图9-4-3(b)所示，其中称为电容的运算容抗，取决于电容电压的初始值，称为附加运算电压。

四、独立电源

对于独立电压源、电流源，只需将相应的电压源电压、电流源电流的时域表达式，经过拉普拉斯变换，得到相应的象函数即可。例如：直流电压源电压变换为；正弦电流源电源变换为。

五、受控电源

对于受控电源，如果控制系数为常数，那么复频域电路模型与其时域电路一样，形式不变。图9-4-4(a)为时域中的VCVS,(b)为其复频域电路模型。其他形式受控电源的复频域电路模型，同理可得。

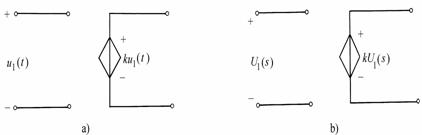
图9-4-4