EEPW论坛

由外加激励和非零初始状态的储能元件的初始储能共同引起的响应，称为全响应，全响应就是微分方程的全解，是方程的特解与其齐次方程的通解之和。

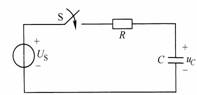
图8-6-1

如图8-6-1所示电路，开关S闭合前，电容两端已有初始电压，在时刻，开关S闭合，后，列写电路的KVL方程：

（式8-6-1）

（式8-6-1）与上一节的（式8-5-1）一样，同理可得：

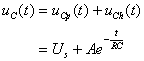（式8-6-2）

根据换路定则：

由（式8-6-2）得：

因此：

最终得到全响应：

（式8-6-3）

现对（式8-6-3）作一个变形，即：

（式8-6-4）

回顾用经典法求解一阶电路过渡过程的步骤，发现一阶电路的全响应总等于对应的一阶线性常系数微分方程的全解，记为，总有：

（式8-6-5）

式中代表方程特解，代表齐次方程的通解，而总为指数形式，则：

（式8-6-6）

取时刻的值：

，

于是得到：

（式8-6-7）

（式8-6-7）就是著名的三要素公式。它是求解一阶动态电路的简便有效的工具。在（式8-6-7）中包含了一阶动态电路的三个要素：

：是一阶线性常系数微分方程的特解，是一阶动态电路在激励作用下的强制分量。当激励是直流或正弦交流电源时，强制分量即是稳态分量，这时候，可按直流电路、正弦交流稳态电路的求解方法求得，；

：是响应在换路后瞬间的初始值，按§8-3节中介绍的方法求解：

：是时间常数，一个一阶电路只有一个时间常数。或，是电路储能元件两端的端口等效电阻。

例8-6-1 如图8-6-2所示电路，，原来打开，C上无电荷。时闭合，求；当时，又闭合，求。

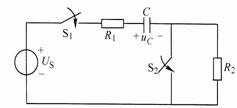
图8-6-2例8-6-1附图

解：由题意知：

根据换路定则：

此处激励为直流，当时，闭合，的稳态值为，即有：

时间常数：

利用三要素公式（式8-6-11）得到：

（V）

当，闭合，有：

在的换路时刻，仍满足换路定则：

在的换路时刻，仍满足换路定则：

的稳态值仍为，则：

时间常数：

又因为换路在进行，延迟了，故而根据三要素公式得到：

（V），

例8-6-2 在图8-6-3所示电路中，，电路已达稳态。时，开关S闭合，求开关S中的过渡电流？

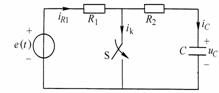
图8-6-3例8-6-2附图

解： ，电路已达稳态，可利用相量计算。由KVL得：

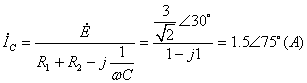
时刻：

根据换路定则：

，且：

画出时刻的等效电路（图略），即可求得：

当后，即是稳态开关电流，此时串联支路被S短接，电容C两端的电荷已放电完毕，故：

时间常数：

（s）

根据三要素公式：