EEPW论坛

建立矩阵形式的回路电流方程组，其推导过程与上节节点电压法相类似。首先定义一个一般性支路（典型支路）如图7-6-1所示，然后写出每一支路的电压电流关系式，并用矩阵形式表示为：

（7-7-1）

当网络不包含受控源时，Z为一对角矩阵。

把式（7-7-1）两边左乘回路矩阵，并考虑到式（7-3-5）与式（7-3-8），可得：

即有：

（7-7-2）

或 ：

（7-7-3）

式中，称为回路阻抗矩阵； 为回路电流列向量。式（7-7-2）与式（7-7-3）即为矩阵形式的回路电流方程。式中各量及可由实际电路及有向图、参考典型支路方向而系统地列写出来。由该矩阵形式的回路电流方程组可解出回路电流值，然后求出各支路电流，再由式（7-7-1）求出各支路电压。

例7-7-1 电路及其有向图如图7-7-1所示，取支路1、2、3为树支，试建立矩阵形式的回路电流方程。

解：选择单连支回路作为基本回路，则可写出基本回路矩阵为：

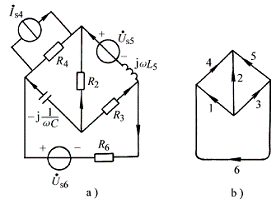
图 7-7-1

支路阻抗矩阵为：

电压源及电流源列向量为：

回路阻抗矩阵为：

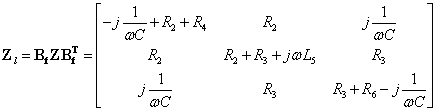
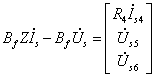
最后可得矩阵形式的回路方程为：

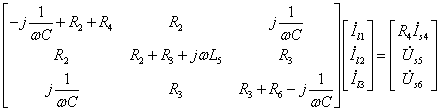
对于具有受控源的电路，如元件电压控制电流源或元件电流控制电压源，其处理方法和节点电压法相同，受控源情况可在列写支路阻抗矩阵Z或支路导纳矩阵Y中加以考虑。由于在采用回路电流法时须预先选择一组独立回路，因此在实际应用中不如节点法方便。