前面已讨论了周期非正弦信号的傅里叶级数展开,下面来分析非周期信号的傅里叶变换。当周期信号的重复周期T无限增大时,周期信号就转化为非周期信号(单个不重复信号),如对于周期矩形脉冲波,当周期T趋于无穷大时,周期信号就转化为单个非周期脉冲。从例6-1-2的结果可知,此时信号频谱间隔![]() 趋于零,即谱线从离散转向连续,而其振幅值则趋于零,信号中各分量都变为无穷小。尽管各频率分量从绝对值来看都趋于无穷小,但其相对大小却是不相同的。为区别这种相对大小,在周期T趋于无穷大时,求
趋于零,即谱线从离散转向连续,而其振幅值则趋于零,信号中各分量都变为无穷小。尽管各频率分量从绝对值来看都趋于无穷小,但其相对大小却是不相同的。为区别这种相对大小,在周期T趋于无穷大时,求![]() 的极限,并定义此极限值为非周期函数的频谱函数
的极限,并定义此极限值为非周期函数的频谱函数![]() ,即:
,即:
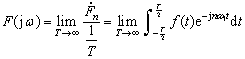
当![]() 时,
时,![]() ,
,![]() 转化为
转化为![]() ,即离散的频谱转为连续频谱,上式可改为:
,即离散的频谱转为连续频谱,上式可改为:
![]() (6-4-1)
(6-4-1)
对于一个非周期信号![]() ,可由上式求出其频谱函数,同理若已知非周期信号频谱函数
,可由上式求出其频谱函数,同理若已知非周期信号频谱函数![]() ,则也可求出其时域表达式。其计算式为:
,则也可求出其时域表达式。其计算式为:
![]() (6-4-2)
(6-4-2)
式(6-4-1)与式(6-4-2)是一对傅里叶积分变换式,式6-4-1把时域信号![]() 转换为频域的频谱函数信号,称为傅里叶正变换。而式6-4-2是把频域信号
转换为频域的频谱函数信号,称为傅里叶正变换。而式6-4-2是把频域信号![]() 变换为时域信号,称为傅里叶逆变换。进行傅里叶变换的函数需满足狄里赫里条件和绝对可积条件。
变换为时域信号,称为傅里叶逆变换。进行傅里叶变换的函数需满足狄里赫里条件和绝对可积条件。
例6-4-1 求图6-4-1a所示的单个矩形波的频谱函数![]() ,并作振幅频谱与相位频谱图。
,并作振幅频谱与相位频谱图。
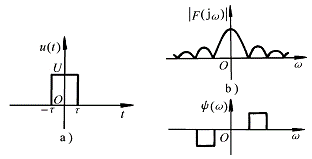
图 6-4-1
解:单个矩形波的频谱函数为:
![]()
![]()
![]()
它的幅度频谱与相位频谱如图6-4-1b、c所示。
从振幅频谱图上可见,矩形脉冲信号所包含的频率分量随频率增大而很快减小,信号主要成份集中于![]() 之间,即频率宽度为
之间,即频率宽度为![]() 。如果脉冲宽度变窄,即值变小,则信号主要频率分量所占的频率范围就变大。反之当脉冲变宽,值变大,则其主要频率分量范围就变小。对于一个较窄的脉冲信号,如果电路要使它通过,则电路的特性必须能使较大频率范围的所有信号都能通过。傅里叶变换在信号分析与处理中有重要意义。
。如果脉冲宽度变窄,即值变小,则信号主要频率分量所占的频率范围就变大。反之当脉冲变宽,值变大,则其主要频率分量范围就变小。对于一个较窄的脉冲信号,如果电路要使它通过,则电路的特性必须能使较大频率范围的所有信号都能通过。傅里叶变换在信号分析与处理中有重要意义。

 我要赚赏金
我要赚赏金

