EEPW论坛

四轴的一个难点在于姿态检测，说到这就不得不提到卡尔曼滤波。

早在1795年，C.F.Gauss为测定行星运行轨道，提出了最小二乘法，最小二乘法的最优指标是估计量测的均方误差最小，没有考虑到被估参数的统计特性；R.A.Fisher于1912年提出最大似然估计法，他从概率密度的角度考虑估计问题，但这种方法没有考虑到先验信息；上世纪40年代，N.Wiener为解决火力控制系统的精确跟踪问题，提出了一种频域设计方法——维纳滤波，该方法的适用范围有限，要求信号一维平稳；1960年，R.E.Kailman提出卡尔曼滤波器，它是一种时域滤波方法，采用状态空间描述系统，算法采用递推机制，数据存储量小，可以处理多维和非平稳过程。

总之，卡尔曼滤波是在离散空间下的最小均方误差准则滤波器，其滤波需要建立较准确的系统和观测模型（最初的卡尔曼滤波不仅要求系统是线性的，并且要求量测方程也是线性的，后人研究了其在非线性条件下的推广，提出了EKF、UKF和CMKF），在每个递推周期中，卡尔曼滤波器需要完成对被估计量的时间更新和量测更新两个过程，时间更新方程旨在实现对系统状态的先验估计，测量方程用于组合先验估计和量测值以获得后验估计，这点有点像贝叶斯估计，即系统决策依赖于后验，而后验又取决于先验和样本。

下面我们用板子采集MPU6050的六轴数据，看看效果，顺便发个冷知识，估计知道的人不多，就是怎么通过仿真器把数据从ARM抓到PC上，这样就免去串口这种又慢又麻烦的方法了。

在DEBUG下，当数据已经采集到ARM的内存中后，暂停CPU运行，点击DEBUG->FUNCTION EDITOR

出现INI的编译窗口，

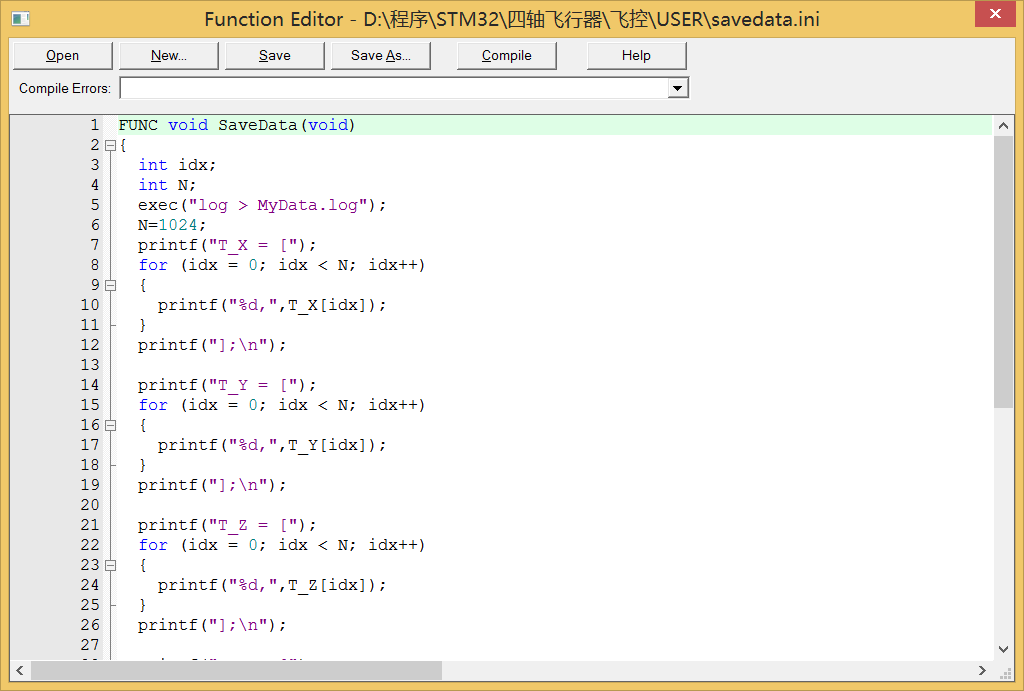
我们处理数据由于是在MATLAB下进行的，所以直接printf按照MATLAB格式输出到txt文件 复制到MATLAB直接用

FUNC void SaveData(void) 
{
  int idx;
	int N;
  exec("log > MyData.log");
	N=1024;
	printf("T_X = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",T_X[idx]);
  }
	printf("];\n");
	
	printf("T_Y = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",T_Y[idx]);
  }
	printf("];\n");
	
	printf("T_Z = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",T_Z[idx]);
  }
	printf("];\n");
	
	printf("G_X = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",G_X[idx]);
  }
	printf("];\n");
	
	printf("G_Y = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",G_Y[idx]);
  }
	printf("];\n");
	
	printf("G_Z = [");
  for (idx = 0; idx < N; idx++) 
	{
    printf("%d,",G_Z[idx]);
  }
	printf("];\n");	
	
  exec("log off");
}

编译成功后，在COMMAND的命令行输入SaveData()，也就是上面函数的函数体，就可以把数据输出到TXT文件，之后就可以把数据弄去处理了。

按照已经建立好的状态空间模型，我们在MATLAB中处理这段6轴数据，得到融合角度。

 P=[0 0;0 0];
    H=[1 dt;0 1];
    T=[dt 0;0 dt];
    Q=[0.01 0;0 0.001];
    R=[0.03 0;0 0.03];

    Klm_Angle_X(i) = Klm_Angle_X(i-1) + bias(i-1) * dt;     %先验计算             
    bias(i) = GYR_X(i);
    
    P=H*P*H'+T*Q*T';            
    
    K=P/(P+R);      %卡尔曼增益计算

    Klm_Angle_X(i)=Klm_Angle_X(i)+K(1,1)*(Angle_X_Acc(i)-Klm_Angle_X(i))+K(1,2)*(GYR_X(i)-bias(i));    %状态预测
    bias(i)=bias(i)+K(2,1)*(Angle_X_Acc(i)-Klm_Angle_X(i))+K(2,2)*(GYR_X(i)-bias(i));
    
    P=P-K*P;                     

绿色是加速度得到的角度，蓝色是陀螺仪得到的角度，红色是一阶互补滤波得到的结果，黑色是卡尔曼滤波的结果

顺带几张细节图

可以看到动态过程中加速度的噪声非常大，静态过程中陀螺仪的漂移的影响非常大，这也就是进行数据融合的原因。

并且，我们可以得到这几种滤波器的优缺点：

<1>互补滤波 优点是计算简单，缺点是一阶互补滤波收敛性与滤波效果不能同时满足，要么静态不容易收敛到加速度计的角度，要么动态滤波中效果不好，如果一定要用互补滤波的话，需要一个很好的折中，二阶互补滤波虽然这两点能满足了，但是又存在一个时延，有时候这个时延是很致命的。

<2>卡尔曼滤波 优点是各项指标都非常好，缺点就是计算量略大。

这个帖子比较NB，另辟蹊径。

设精！