EEPW论坛

1、四个概念：“地理”坐标系、“机体”坐标系、他们之间换算公式、换算公式用的系数。

地理坐标系：东、北、天，以下简称地理。在这个坐标系里有重力永远是（0,0,1g），地磁永远是（0,1,x）（地磁的垂直不关心）两个三维向量。
机体坐标系：以下简称机体，上面有陀螺、加计、电子罗盘传感器，三个三维向量。
换算公式：以下简称公式，公式就是描述机体姿态的表达方法，一般都是用以地理为基准，从地理换算到机体的公式，有四元数、欧拉角、方向余弦矩阵。
换算公式的系数：以下简称系数，四元数的q0123、欧拉角的ROLL/PITCH/YAW、余弦矩阵的9个数。系数就是描述机体姿态的表达方法的具体数值。

姿态，其实就是公式+系数的组合，一般经常用人容易理解的公式“欧拉角”表示，系数就是横滚xx度俯仰xx度航向xx度。

2、五个数据源：重力、地磁、陀螺、加计、电子罗盘，前两个来自地理，后三个来自机体。

3、陀螺向量：基于机体，也在机体上积分，因为地理上无参考数据源，所以很独立，直接在公式的老系数上积分，得到新系数。
狭义上的捷联惯导算法，就是指这个陀螺积分公式，也分为欧拉角、方向余弦矩阵、四元数，他们的积分算法有增量法、数值积分法（X阶龙格-库塔）等等

4、加计向量、重力向量：加计基于机体，重力基于地理，重力向量（0,0,1g）用公式换算到机体，与机体的加计向量算出误差。理论上应该没有误差，这误差逆向思维一下，其实就是换算公式的系数误差。所以这误差可用于纠正公式的系数（横滚、俯仰），也就是姿态。

5、电子罗盘向量、地磁向量：同上，只不过要砍掉地理上的垂直向量，因为无用。只留下地理水平面上的向量。误差可以用来纠正公式的系数（航向）。

6、就这样，系数不停地被陀螺积分更新，也不停地被误差修正，它和公式所代表的姿态也在不断更新。
如果积分和修正用四元数算法（因为运算量较少、无奇点误差），最后用欧拉角输出控制PID（因为角度比较直观），那就需要有个四元数系数到欧拉角系数的转换。常用的三种公式，它们之间都有转换算法。

再搞个直白一点的例子：
机体好似一条船，地理就是那地图，姿态就是航向（船头在地图上的方位），重力和地磁是地图上的灯塔，陀螺/积分公式是舵手，加计和电子罗盘是瞭望手。
舵手负责估计和把稳航向，他相信自己，本来船向北开的，就一定会一直往北开，觉得转了90度弯，那就会往东开。
当然如果舵手很牛逼，也许能估计很准确，维持很长时间。不过只信任舵手，肯定会迷路，所以一般都有地图和瞭望手来观察误差。
瞭望手根据地图灯塔方位和船的当前航向，算出灯塔理论上应该在船的X方位。然而看到实际灯塔在船的Y方位，那肯定船的当前航向有偏差了，偏差就是ERR=X-Y。
舵手收到瞭望手给的ERR报告，觉得可靠，那就听个90%*ERR，觉得天气不好、地图误差大，那就听个10%*ERR，根据这个来纠正估算航向。。



------------------------------------------------------
来点干货，注意以下的欧拉角都是这样的顺序：先航向-再俯仰-然后横滚
公式截图来自：袁信、郑锷的《捷联式惯性导航原理》，邓正隆的《惯性技术》。
--------------------------------------------------
根据加计计算初始欧拉角
这个无论欧拉角算法还是四元数算法还是方向余弦矩阵都需要，因为加计和电子罗盘给出欧拉角的描述方式比较方便。
imu.euler.x = atan2(imu.accel.y, imu.accel.z);
imu.euler.y = -asin(imu.accel.x / ACCEL_1G);
ACCEL_1G 为9.81米/秒^2，accel.xyz的都为这个单位，算出来的euler.xyz单位是弧度
航向imu.euler.z可以用电子罗盘计算
--------------------------------------------------
欧拉角微分方程
如果用欧拉角算法，那么这个公式就够了，不需要来回转换。
 
矩阵上到下三个角度（希腊字母）是roll pitch和yaw，公式最左边的上面带点的三个是本次更新后的角度，不带点的是上个更新周期算出来的角度。
Wx,y,z是roll pitch和yaw方向的三个陀螺在这个周期转动过的角度，单位为弧度，计算为间隔时间T*陀螺角速度,比如0.02秒*0.01弧度/秒=0.0002弧度.


--------------------------------------------------
以下是四元数
--------------------------------------------------
四元数初始化
q0-3为四元数四个值,用最上面公式根据加计计算出来的欧拉角来初始化
 
--------------------------------------------------
四元数微分方程
四元数更新算法，一阶龙库法，同样4个量（入、P1-3）也为四元数的四个值,即上面的q0-3。
Wx,y,z是三个陀螺的这个周期的角速度，比如欧拉角微分方程中的0.01弧度/秒，T为更新周期,比如上面的0.02秒。
 
再来一张，另外一本书上的，仔细看和上面是一样的delta角度，就是上面的角速度*周期，单位为弧度
 
--------------------------------------------------
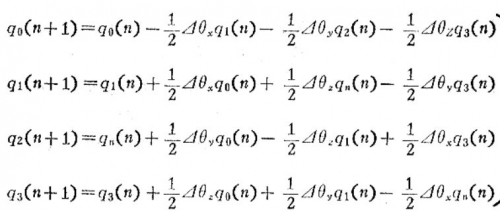
四元数微分方程更新后的规范化
每个周期更新完四元数，需要对四元数做规范化处理。因为四元数本来就定义为四维单位向量。
求q0-3的平方和，再开根号算出的向量长度length。然后每个q0-3除这个length。
 
--------------------------------------------------
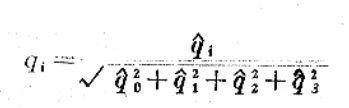
四元数转欧拉角公式
把四元数转成了方向余弦矩阵中的几个元素，再用这几个元素转成了欧拉角
先从四元数q0-3转成方向余弦矩阵：
 
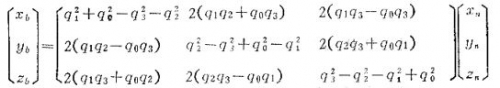
再从方向余弦矩阵转成欧拉角
 

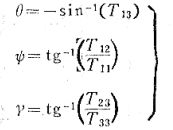
代码：
        //更新方向余弦矩阵
        t11=q.q0*q.q0+q.q1*q.q1-q.q2*q.q2-q.q3*q.q3;
        t12=2.0*(q.q1*q.q2+q.q0*q.q3);
        t13=2.0*(q.q1*q.q3-q.q0*q.q2);
        t21=2.0*(q.q1*q.q2-q.q0*q.q3);
        t22=q.q0*q.q0-q.q1*q.q1+q.q2*q.q2-q.q3*q.q3;
        t23=2.0*(q.q2*q.q3+q.q0*q.q1);
        t31=2.0*(q.q1*q.q3+q.q0*q.q2);
        t32=2.0*(q.q2*q.q3-q.q0*q.q1);
        t33=q.q0*q.q0-q.q1*q.q1-q.q2*q.q2+q.q3*q.q3;
        //求出欧拉角
        imu.euler.roll = atan2(t23,t33);
        imu.euler.pitch = -asin(t13);
        imu.euler.yaw = atan2(t12,t11);
        if (imu.euler.yaw < 0){
                imu.euler.yaw += ToRad(360);
        }
----------------------------------------------------
以下代码摘自网上，很巧妙，附上注释，有四元数微分，有加计耦合。
没电子罗盘，其实耦合原理也一样。

//=====================================================================================================
// IMU.c
// S.O.H. Madgwick
// 25th September 2010
//=====================================================================================================
// Description:
//
// Quaternion implementation of the 'DCM filter' [Mayhony et al].
//
// User must define 'halfT' as the (sample period / 2), and the filter gains 'Kp' and 'Ki'.
//
// Global variables 'q0', 'q1', 'q2', 'q3' are the quaternion elements representing the estimated
// orientation.  See my report for an overview of the use of quaternions in this application.
//
// User must call 'IMUupdate()' every sample period and parse calibrated gyroscope ('gx', 'gy', 'gz')
// and accelerometer ('ax', 'ay', 'ay') data.  Gyroscope units are radians/second, accelerometer
// units are irrelevant as the vector is normalised.
//
//=====================================================================================================

//----------------------------------------------------------------------------------------------------
// Header files

#include "IMU.h"
#include <math.h>

//----------------------------------------------------------------------------------------------------
// Definitions

#define Kp 2.0f                        // proportional gain governs rate of convergence to accelerometer/magnetometer
#define Ki 0.005f                // integral gain governs rate of convergence of gyroscope biases
#define halfT 0.5f                // half the sample period

//---------------------------------------------------------------------------------------------------
// Variable definitions

float q0 = 1, q1 = 0, q2 = 0, q3 = 0;        // quaternion elements representing the estimated orientation
float exInt = 0, eyInt = 0, ezInt = 0;        // scaled integral error

//====================================================================================================
// Function
//====================================================================================================

void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az) {
        float norm;
        float vx, vy, vz;
        float ex, ey, ez;         
       
        // normalise the measurements
        norm = sqrt(ax*ax + ay*ay + az*az);      
        ax = ax / norm;
        ay = ay / norm;
        az = az / norm;      
把加计的三维向量转成单位向量。
       

        // estimated direction of gravity
        vx = 2*(q1*q3 - q0*q2);
        vy = 2*(q0*q1 + q2*q3);
        vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;

这是把四元数换算成《方向余弦矩阵》中的第三列的三个元素。
根据余弦矩阵和欧拉角的定义，地理坐标系的重力向量，转到机体坐标系，正好是这三个元素。
所以这里的vx\y\z，其实就是当前的欧拉角（即四元数）的机体坐标参照系上，换算出来的重力单位向量。


        // error is sum of cross product between reference direction of field and direction measured by sensor
        ex = (ay*vz - az*vy);
        ey = (az*vx - ax*vz);
        ez = (ax*vy - ay*vx);

axyz是机体坐标参照系上，加速度计测出来的重力向量，也就是实际测出来的重力向量。
axyz是测量得到的重力向量，vxyz是陀螺积分后的姿态来推算出的重力向量，它们都是机体坐标参照系上的重力向量。
那它们之间的误差向量，就是陀螺积分后的姿态和加计测出来的姿态之间的误差。
向量间的误差，可以用向量叉积（也叫向量外积、叉乘）来表示，exyz就是两个重力向量的叉积。
这个叉积向量仍旧是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，正好拿来纠正陀螺。（你可以自己拿东西想象一下）由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。



        // integral error scaled integral gain
        exInt = exInt + ex*Ki;
        eyInt = eyInt + ey*Ki;
        ezInt = ezInt + ez*Ki;

        // adjusted gyroscope measurements
        gx = gx + Kp*ex + exInt;
        gy = gy + Kp*ey + eyInt;
        gz = gz + Kp*ez + ezInt;

用叉积误差来做PI修正陀螺零偏




        // integrate quaternion rate and normalise
        q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
        q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
        q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
        q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;  
四元数微分方程

       

        // normalise quaternion
        norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
        q0 = q0 / norm;
        q1 = q1 / norm;
        q2 = q2 / norm;
        q3 = q3 / norm;
四元数规范化
}

//====================================================================================================
// END OF CODE
//====================================================================================================