包含一个电容和电感,或两个电容,或两个电感(两个电容在电路中不能构成串并联或与电压源构成回路,两个电感也有类似要求)的动态电路称为二阶电路。
从最简单的LC电路的零输入响应开始。电路如下:
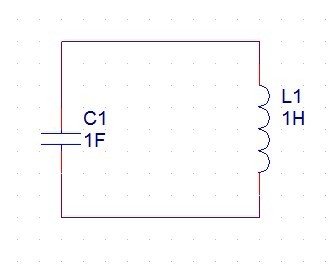
设初始状态下,电容电压为U,电感电流为零。因为电感电压必须等于电容电压,所以电流的变化率不为零。即: 。因此电流将开始增加,储存于电容中的能量将转移到电感中。
。因此电流将开始增加,储存于电容中的能量将转移到电感中。
当电容电压下降到零的瞬间,电感电压也为零,此时: ,电流达到最大值I。虽然电容电压为零,但是其变化率不为零,因为电容中的电流必须等于电感中的电流。因此,电容会被慢慢充电,只是电压极性和初始相反。。。。。。
,电流达到最大值I。虽然电容电压为零,但是其变化率不为零,因为电容中的电流必须等于电感中的电流。因此,电容会被慢慢充电,只是电压极性和初始相反。。。。。。
由此可见,在LC电路中,能量始终在电场和磁场间转换。可以想到,如果没有电阻进行衰减,该振荡将一直保持下去。
根据VAR,可以得到该电路的二阶微分方程:
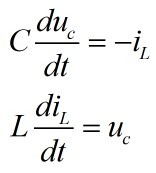
已知初始条件:![]()
归一化处理,设C=1F,L=1H。不难得到:
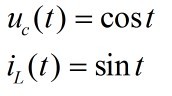 该式表明,LC回路中的振荡是按正弦方式随时间变化的。
该式表明,LC回路中的振荡是按正弦方式随时间变化的。
LC回路中的储能:
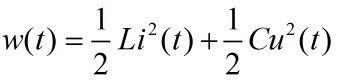
代入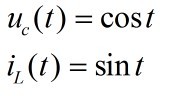 (此时L=C=1):
(此时L=C=1):
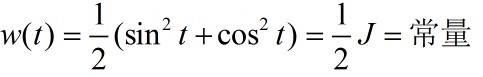
这就表明:储能不断的在电场和磁场之间往返,永不消逝。

 我要赚赏金
我要赚赏金

