EEPW论坛

　　归并排序也称合并排序，其算法思想是将待排序序列分为两部分，依次对分得的两个部分再次使用归并排序，之后再对其进行合并。仅从算法思想上了解归并排序会觉得很抽象，接下来就以对序列A[0], A[l]…, A[n-1]进行升序排列来进行讲解，在此采用自顶向下的实现方法，操作步骤如下。

　　(1)将所要进行的排序序列分为左右两个部分，如果要进行排序的序列的起始元素下标为first，最后一个元素的下标为last，那么左右两部分之间的临界点下标mid=(first+last)/2，这两部分分别是A[first … mid]和A[mid+1 … last]。

　　(2)将上面所分得的两部分序列继续按照步骤(1)继续进行划分，直到划分的区间长度为1。

　　(3)将划分结束后的序列进行归并排序，排序方法为对所分的n个子序列进行两两合并，得到n/2或n/2+l个含有两个元素的子序列，再对得到的子序列进行合并，直至得到一个长度为n的有序序列为止。下面通过一段代码来看如何实现归并排序。

#include <stdio.h>
#include <stdlib.h>
#define N 7

void merge(int arr[], int low, int mid, int high){
    int i, k;
    int *tmp = (int *)malloc((high-low+1)*sizeof(int));
    //申请空间，使其大小为两个
    int left_low = low;
    int left_high = mid;
    int right_low = mid + 1;
    int right_high = high;

    for(k=0; left_low<=left_high && right_low<=right_high; k++){  // 比较两个指针所指向的元素
        if(arr[left_low]<=arr[right_low]){
            tmp[k] = arr[left_low++];
        }else{
            tmp[k] = arr[right_low++];
        }
    }

    if(left_low <= left_high){  //若第一个序列有剩余，直接复制出来粘到合并序列尾
    //memcpy(tmp+k, arr+left_low, (left_high-left_low+l)*sizeof(int));
    for(i=left_low;i<=left_high;i++)
        tmp[k++] = arr[i];
    }

    if(right_low <= right_high){
    //若第二个序列有剩余，直接复制出来粘到合并序列尾
    //memcpy(tmp+k, arr+right_low, (right_high-right_low+1)*sizeof(int));
        for(i=right_low; i<=right_high; i++)
            tmp[k++] = arr[i];
    }

    for(i=0; i<high-low+1; i++)
        arr[low+i] = tmp[i];
    free(tmp);
    return;
}

void merge_sort(int arr[], unsigned int first, unsigned int last){
    int mid = 0;
    if(first<last){
        mid = (first+last)/2; /* 注意防止溢出 */
        /*mid = first/2 + last/2;*/
        //mid = (first & last) + ((first ^ last) >> 1);
        merge_sort(arr, first, mid);
        merge_sort(arr, mid+1,last);
        merge(arr,first,mid,last);
    }
    return;
}

int main(){
    int i;
    int a[N]={32,12,56,78,76,45,36};

    printf ("排序前 \n");
    for(i=0;i<N;i++)
        printf("%d\t",a[i]);

    merge_sort(a,0,N-1);  // 排序

    printf ("\n 排序后 \n");
    for(i=0;i<N;i++)
        printf("%d\t",a[i]); printf("\n");

    system("pause");
    return 0;
}

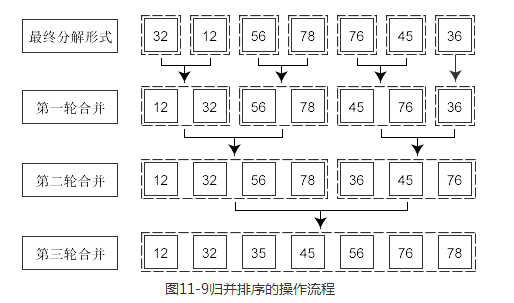
　　分析上面的运行结果，通过归并排序成功地实现了对给定序列的排序操作。接下来通过图11-9来了解归并排序的具体操作流程。

　　在图11-9中，先对所要进行排序的序列进行分解，直到分为单个元素为止，然后将其进行两两合并。由于最终分解成单个元素，因此在合并的时候.将小数放在前面，大数放在后面，得到一个有序序列。接下来对两个相连的有序序列进行排序，先比较有序序列中的第一个元素，将较小的元素放入临时数组中，接着将较小元素所在数组的下一个元素与另一个数组中的较小元素比较，同样将较小元素放入临时数组中，依次进行，直到两个数组的所有元素都放入临时数组中，最后再将临时数组的元素放入原始数组中的对应位置。