基本概念
块统计的关键概念是：任何尺寸的正方形印刷电路板走线(厚度确定)的电阻值都与其它尺寸的方块相同。正方块的电阻值只取决于导电材料的电阻率及其厚度。这一概念可适用于任何类型的导电材料。表1给出了一些常见的半导体材料以及它们的体电阻率。
对印刷电路板而言，最重要的材料就是铜，它是大多数电路板的制造原料(注意：铝用于集成电路片芯的金属化，本文原理同样适用于铝)。我们先从图1中的铜方块说起。该铜块的长度为L，宽度也为L(因为是正方形)，厚度为t，电流通过的铜箔区截面积为A。该铜块的电阻可简单表示为R=ρL/A，其中，ρ是铜的电阻率(这是材料的固有特性，在25℃时为0.67μΩ/in.)。
但注意，截面A是长度L与厚度t的乘积(A=Lt)。分母中的L与分子中的L相互消去，只留下R=ρ/t。因此，铜块的电阻与方块的尺寸无关，它只取决于材料的电阻率与厚度。如果我们知道任何尺寸铜方块的电阻值，并可将需要估算的整条走线分解成多个方块，就可加算(统计)方块数量，从而得出走线的总电阻。实现要实现这一技术，我们只需要一个表，表中给出了印刷电路板走线上一个方块的电阻值与铜箔厚度之间的函数关系。铜箔厚度一般用铜箔重量来指定。例如，1oz.铜指的是每平方英尺重量为1oz.。表2给出了四种最常用铜箔的重量以及它们在25℃和100℃时的电阻率。请注意，由于材料具有正温度系数，铜电阻值会随温度的升高而增加。打个比方，我们现在知道一块0.5oz.重的方形铜箔的电阻大约为1mΩ，这个值与方块的尺寸无关。如果我们能把需要测算的印刷电路板走线分解为多个虚拟的方块，然后把这些方块加总起来，就得到了走线的电阻。
一个简单的例子
我们举一个简单的例子。图2是一条长方形的铜走线，在25℃时其重量约为0.5oz.，走线宽度为1英寸，长度为12英寸。我们可以将走线分解成一系列方块，每个方块边长都是1英寸。这样，总共就有12个方块。按照表2，每个0.5oz.重的铜箔方块的电阻为1mΩ，现在共有12个方块，因此走线的总电阻为12mΩ。
首先要知道，在前面的例子中，我们假定电流是沿方块的一边呈直线流动，从一端流向另一端(如图3a所示)。然而，如果电流要拐个直角弯(如图3b中的方形直角)，那情况就有些不同了。在前面的例子中，我们假定电流是沿方块的一边呈直线流动，从一端流向另一端(如图3a所示)。如果电流要拐个直角弯(如图3b中的方形直角)，我们会发现，方块左下方部分的电流路径要短于右上方部分。当电流流过拐角时，电流密度较高，这意味着一个拐角方块的电阻只能按0.56个正方形来计算。现在我们看到，方块左下方部分的电流路径要短于右上方部分。因此，电流会拥挤在电阻较低的左下方区域。所以，这个区域的电流密度就会高于右上方区域。箭头之间的距离表示了电流密度的差异。结果是，一个拐角方块的电阻只相当于0.56个正方形(图4)。
同样，我们可对焊在印刷电路板上的连接器做一些修正。在这里，我们假设，与铜箔电阻相比，连接器电阻可忽略不计。我们可以看到，如果连接器占据了待评估铜箔区域中很大一部分，则该区域的电阻就应相应降低。图5显示了三端连接器结构及其等效方块的计算(参考文献1)。阴影区表示铜箔区内的连接器管脚。
一个更复杂的例子
我们共有六个完全正方块，两个包括连接器的正方块，还有三个拐角方块。由于1oz.铜箔的电阻为0.5mΩ/方块，并且电流线性地流过六个全方块，这些方块的总电阻为：6×0.5mΩ=3mΩ。然后，我们要加上两个有连接器的方块，每个按0.14个方块计算(图5c)。因此，两个连接器算0.28个方块(2×0.14)。对于1oz.铜箔，这增加了0.14mΩ的电阻(0.28×0.5mΩ=0.14mΩ)。最后，加上三个拐角方块。每个按0.56个方块计算，总共为3×0.56×0.5mΩ=0.84mΩ。因此，从A到B的总电阻为3.98mΩ(3mΩ+0.14mΩ+0.84mΩ)。总结如下
●六个为1的全正方形=6个等效方块;两个为0.14的连接器方块=0.28个等效方块;三个为0.56的角方块=1.68个等效方块●总等效方块数=7.96个等效方块●电阻(A到B)=7.96个方块的电阻，因每方块为0.5mΩ，于是总电阻=3.98mΩ这一技术可以方便地应用至复杂的几何形状。一旦知道了某根走线的电阻值，想算其它量(如电压降或功耗等)就很简单了。过孔怎么算?
印刷电路板通常都不限于单层，而是以不同层的方式堆叠起来。过孔用于不同层之间的走线连接。每个过孔的电阻有限，在走线总电阻计算时必须将过孔的电阻考虑在内。一般而言，当过孔连接两根走线(或平面)时，它就构成了一个串联电阻元件。经常采用多个并联过孔的方法，以降低有效电阻。过孔电阻的计算基于图7所示的简化过孔几何形状。沿着过孔长度(L)方向的电流(如箭头所指)穿过一个截面积区域(A)。厚度(t)取决于过孔内壁电镀的铜层厚度。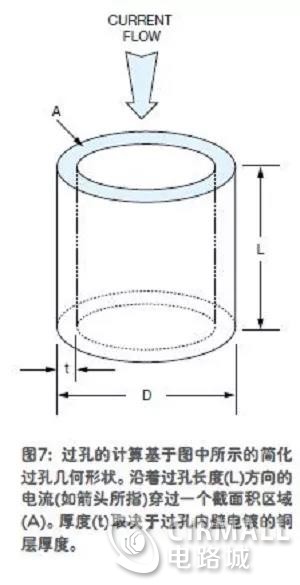
经过一些简单的代数变换，过孔电阻可表示为R=ρL/[π(Dt-t2)]，其中，ρ是镀铜的电阻率(25℃下为2.36μΩ/in.)。注意，镀铜的电阻率远高于纯铜的电阻率。我们假设，过孔中镀层的厚度t一般为1mil，它与电路板的铜箔重量无关。对于一个10层板，层厚为3.5mil，铜重量为2oz.时，L大约为63mil。
基于上述假设，表3给出了常见过孔尺寸及其电阻。我们可以针对自身特殊的板厚，调整这些数值的高低。另外，网上也有许多免费易用的过孔计算程序。以上就是一种估算印刷电路板走线或平面直流电阻的简单方法。复杂的几何形状可以分解成多个不同尺寸的铜方块，以近似于整个铜箔区。一旦确定了铜箔的重量，则任何尺寸方块的电阻值就都是已知量了。这样，估算过程就简化为单纯的铜方块数量统计。
STM32
MCU
通讯及无线技术
物联网技术
电子DIY
板卡试用
基础知识
软件与操作系统
我爱生活
小e食堂